Facilitating Battery Swapping Services for Freight Trucks with Spatial-Temporal Demand Prediction

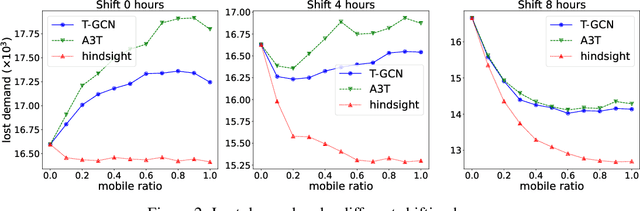
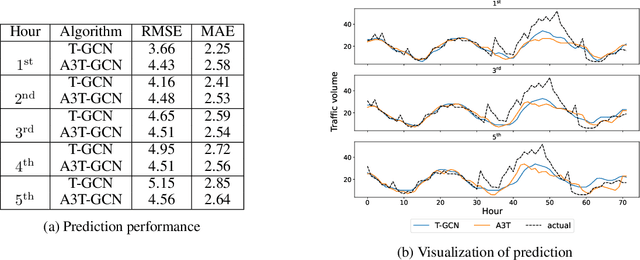
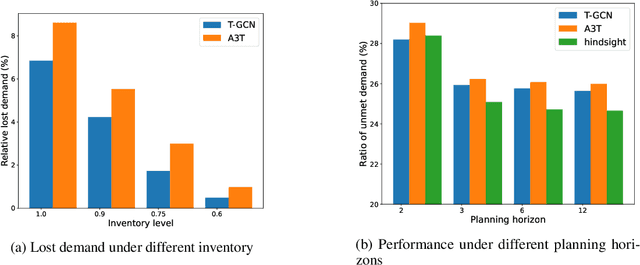
Electrifying heavy-duty trucks offers a substantial opportunity to curtail carbon emissions, advancing toward a carbon-neutral future. However, the inherent challenges of limited battery energy and the sheer weight of heavy-duty trucks lead to reduced mileage and prolonged charging durations. Consequently, battery-swapping services emerge as an attractive solution for these trucks. This paper employs a two-fold approach to investigate the potential and enhance the efficacy of such services. Firstly, spatial-temporal demand prediction models are adopted to predict the traffic patterns for the upcoming hours. Subsequently, the prediction guides an optimization module for efficient battery allocation and deployment. Analyzing the heavy-duty truck data on a highway network spanning over 2,500 miles, our model and analysis underscore the value of prediction/machine learning in facilitating future decision-makings. In particular, we find that the initial phase of implementing battery-swapping services favors mobile battery-swapping stations, but as the system matures, fixed-location stations are preferred.

Uniform Convergence with Square-Root Lipschitz Loss

We establish generic uniform convergence guarantees for Gaussian data in terms of the Rademacher complexity of the hypothesis class and the Lipschitz constant of the square root of the scalar loss function. We show how these guarantees substantially generalize previous results based on smoothness (Lipschitz constant of the derivative), and allow us to handle the broader class of square-root-Lipschitz losses, which includes also non-smooth loss functions appropriate for studying phase retrieval and ReLU regression, as well as rederive and better understand "optimistic rate" and interpolation learning guarantees.

Fair Representation Clustering with Several Protected Classes

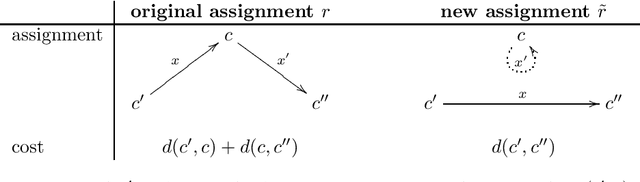
We study the problem of fair $k$-median where each cluster is required to have a fair representation of individuals from different groups. In the fair representation $k$-median problem, we are given a set of points $X$ in a metric space. Each point $x\in X$ belongs to one of $\ell$ groups. Further, we are given fair representation parameters $\alpha_j$ and $\beta_j$ for each group $j\in [\ell]$. We say that a $k$-clustering $C_1, \cdots, C_k$ fairly represents all groups if the number of points from group $j$ in cluster $C_i$ is between $\alpha_j |C_i|$ and $\beta_j |C_i|$ for every $j\in[\ell]$ and $i\in [k]$. The goal is to find a set $\mathcal{C}$ of $k$ centers and an assignment $\phi: X\rightarrow \mathcal{C}$ such that the clustering defined by $(\mathcal{C}, \phi)$ fairly represents all groups and minimizes the $\ell_1$-objective $\sum_{x\in X} d(x, \phi(x))$. We present an $O(\log k)$-approximation algorithm that runs in time $n^{O(\ell)}$. Note that the known algorithms for the problem either (i) violate the fairness constraints by an additive term or (ii) run in time that is exponential in both $k$ and $\ell$. We also consider an important special case of the problem where $\alpha_j = \beta_j = \frac{f_j}{f}$ and $f_j, f \in \mathbb{N}$ for all $j\in [\ell]$. For this special case, we present an $O(\log k)$-approximation algorithm that runs in $(kf)^{O(\ell)}\log n + poly(n)$ time.

Is Local SGD Better than Minibatch SGD?

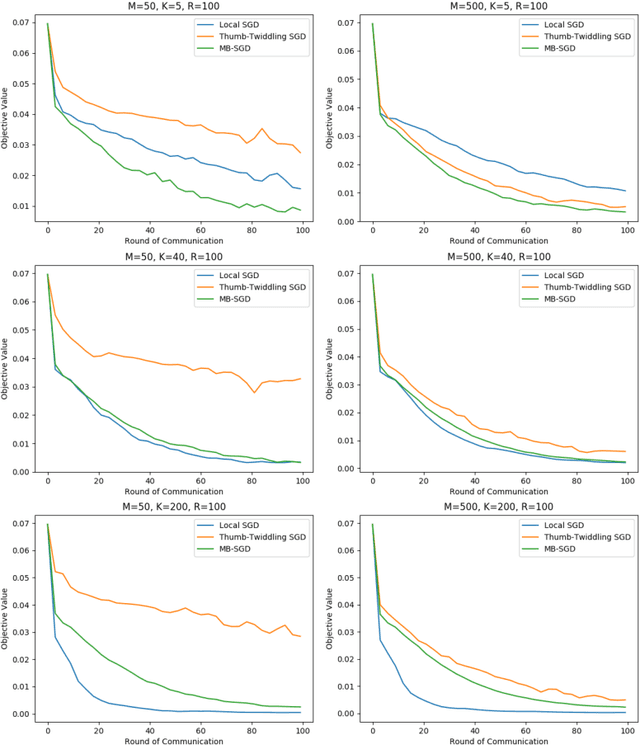
We study local SGD (also known as parallel SGD and federated averaging), a natural and frequently used stochastic distributed optimization method. Its theoretical foundations are currently lacking and we highlight how all existing error guarantees in the convex setting are dominated by a simple baseline, minibatch SGD. (1) For quadratic objectives we prove that local SGD strictly dominates minibatch SGD and that accelerated local SGD is minimax optimal for quadratics; (2) For general convex objectives we provide the first guarantee that at least sometimes improves over minibatch SGD; (3) We show that indeed local SGD does not dominate minibatch SGD by presenting a lower bound on the performance of local SGD that is worse than the minibatch SGD guarantee.