Kumar Kshitij Patel
Personalized Federated Training of Diffusion Models with Privacy Guarantees
Apr 01, 2025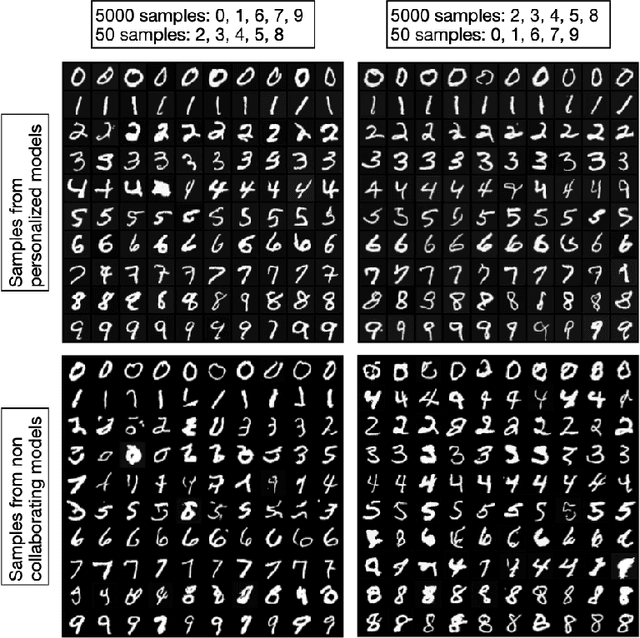
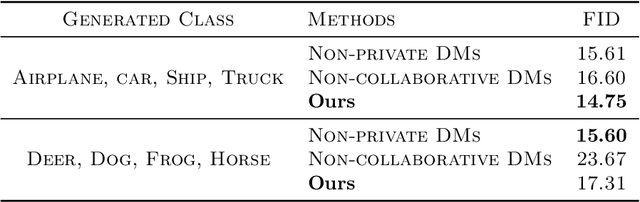


Abstract:The scarcity of accessible, compliant, and ethically sourced data presents a considerable challenge to the adoption of artificial intelligence (AI) in sensitive fields like healthcare, finance, and biomedical research. Furthermore, access to unrestricted public datasets is increasingly constrained due to rising concerns over privacy, copyright, and competition. Synthetic data has emerged as a promising alternative, and diffusion models -- a cutting-edge generative AI technology -- provide an effective solution for generating high-quality and diverse synthetic data. In this paper, we introduce a novel federated learning framework for training diffusion models on decentralized private datasets. Our framework leverages personalization and the inherent noise in the forward diffusion process to produce high-quality samples while ensuring robust differential privacy guarantees. Our experiments show that our framework outperforms non-collaborative training methods, particularly in settings with high data heterogeneity, and effectively reduces biases and imbalances in synthetic data, resulting in fairer downstream models.
Approaching Deep Learning through the Spectral Dynamics of Weights
Aug 21, 2024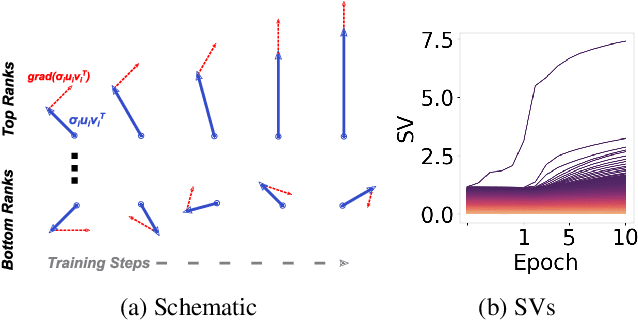
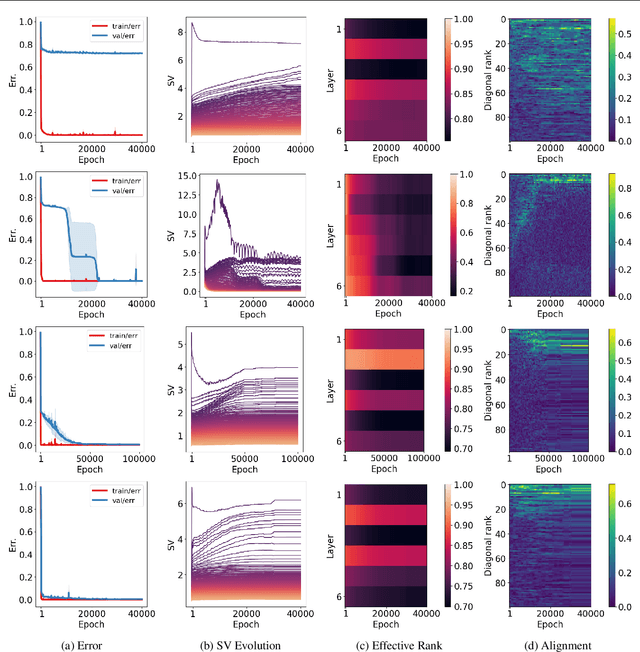
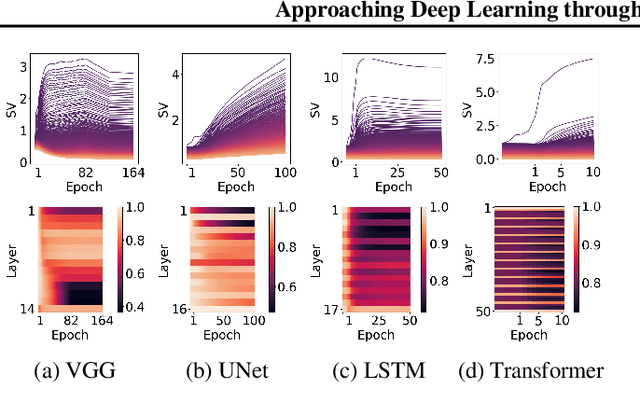
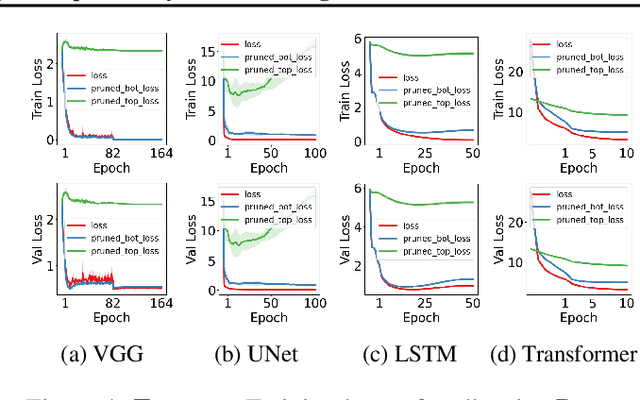
Abstract:We propose an empirical approach centered on the spectral dynamics of weights -- the behavior of singular values and vectors during optimization -- to unify and clarify several phenomena in deep learning. We identify a consistent bias in optimization across various experiments, from small-scale ``grokking'' to large-scale tasks like image classification with ConvNets, image generation with UNets, speech recognition with LSTMs, and language modeling with Transformers. We also demonstrate that weight decay enhances this bias beyond its role as a norm regularizer, even in practical systems. Moreover, we show that these spectral dynamics distinguish memorizing networks from generalizing ones, offering a novel perspective on this longstanding conundrum. Additionally, we leverage spectral dynamics to explore the emergence of well-performing sparse subnetworks (lottery tickets) and the structure of the loss surface through linear mode connectivity. Our findings suggest that spectral dynamics provide a coherent framework to better understand the behavior of neural networks across diverse settings.
The Limitations of Model Retraining in the Face of Performativity
Aug 16, 2024Abstract:We study stochastic optimization in the context of performative shifts, where the data distribution changes in response to the deployed model. We demonstrate that naive retraining can be provably suboptimal even for simple distribution shifts. The issue worsens when models are retrained given a finite number of samples at each retraining step. We show that adding regularization to retraining corrects both of these issues, attaining provably optimal models in the face of distribution shifts. Our work advocates rethinking how machine learning models are retrained in the presence of performative effects.
The Limits and Potentials of Local SGD for Distributed Heterogeneous Learning with Intermittent Communication
May 19, 2024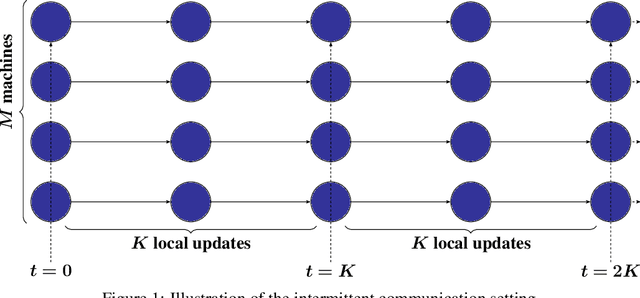

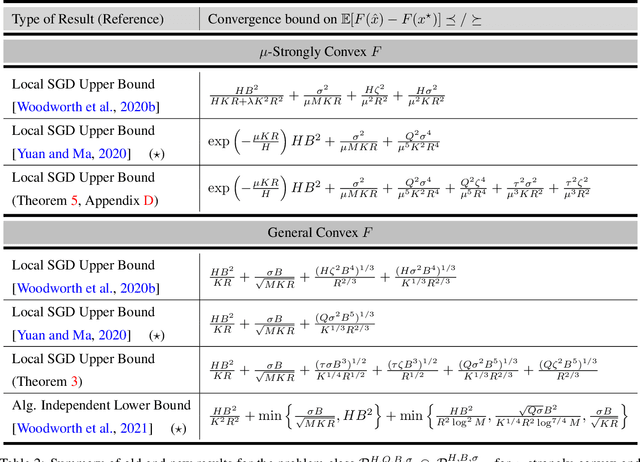
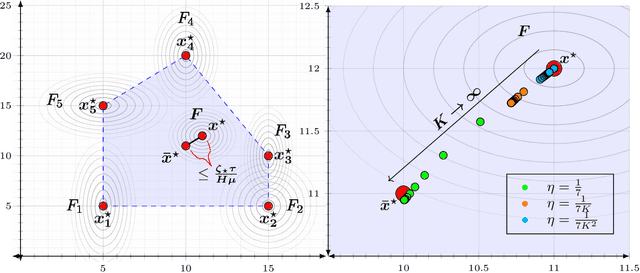
Abstract:Local SGD is a popular optimization method in distributed learning, often outperforming other algorithms in practice, including mini-batch SGD. Despite this success, theoretically proving the dominance of local SGD in settings with reasonable data heterogeneity has been difficult, creating a significant gap between theory and practice. In this paper, we provide new lower bounds for local SGD under existing first-order data heterogeneity assumptions, showing that these assumptions are insufficient to prove the effectiveness of local update steps. Furthermore, under these same assumptions, we demonstrate the min-max optimality of accelerated mini-batch SGD, which fully resolves our understanding of distributed optimization for several problem classes. Our results emphasize the need for better models of data heterogeneity to understand the effectiveness of local SGD in practice. Towards this end, we consider higher-order smoothness and heterogeneity assumptions, providing new upper bounds that imply the dominance of local SGD over mini-batch SGD when data heterogeneity is low.
Federated Online and Bandit Convex Optimization
Nov 29, 2023Abstract:We study the problems of distributed online and bandit convex optimization against an adaptive adversary. We aim to minimize the average regret on $M$ machines working in parallel over $T$ rounds with $R$ intermittent communications. Assuming the underlying cost functions are convex and can be generated adaptively, our results show that collaboration is not beneficial when the machines have access to the first-order gradient information at the queried points. This is in contrast to the case for stochastic functions, where each machine samples the cost functions from a fixed distribution. Furthermore, we delve into the more challenging setting of federated online optimization with bandit (zeroth-order) feedback, where the machines can only access values of the cost functions at the queried points. The key finding here is identifying the high-dimensional regime where collaboration is beneficial and may even lead to a linear speedup in the number of machines. We further illustrate our findings through federated adversarial linear bandits by developing novel distributed single and two-point feedback algorithms. Our work is the first attempt towards a systematic understanding of federated online optimization with limited feedback, and it attains tight regret bounds in the intermittent communication setting for both first and zeroth-order feedback. Our results thus bridge the gap between stochastic and adaptive settings in federated online optimization.
On the Effect of Defections in Federated Learning and How to Prevent Them
Nov 28, 2023Abstract:Federated learning is a machine learning protocol that enables a large population of agents to collaborate over multiple rounds to produce a single consensus model. There are several federated learning applications where agents may choose to defect permanently$-$essentially withdrawing from the collaboration$-$if they are content with their instantaneous model in that round. This work demonstrates the detrimental impact of such defections on the final model's robustness and ability to generalize. We also show that current federated optimization algorithms fail to disincentivize these harmful defections. We introduce a novel optimization algorithm with theoretical guarantees to prevent defections while ensuring asymptotic convergence to an effective solution for all participating agents. We also provide numerical experiments to corroborate our findings and demonstrate the effectiveness of our algorithm.
A Stochastic Newton Algorithm for Distributed Convex Optimization
Oct 07, 2021



Abstract:We propose and analyze a stochastic Newton algorithm for homogeneous distributed stochastic convex optimization, where each machine can calculate stochastic gradients of the same population objective, as well as stochastic Hessian-vector products (products of an independent unbiased estimator of the Hessian of the population objective with arbitrary vectors), with many such stochastic computations performed between rounds of communication. We show that our method can reduce the number, and frequency, of required communication rounds compared to existing methods without hurting performance, by proving convergence guarantees for quasi-self-concordant objectives (e.g., logistic regression), alongside empirical evidence.
Minibatch vs Local SGD for Heterogeneous Distributed Learning
Jun 18, 2020


Abstract:We analyze Local SGD (aka parallel or federated SGD) and Minibatch SGD in the heterogeneous distributed setting, where each machine has access to stochastic gradient estimates for a different, machine-specific, convex objective; the goal is to optimize w.r.t. the average objective; and machines can only communicate intermittently. We argue that, (i) Minibatch SGD (even without acceleration) dominates all existing analysis of Local SGD in this setting, (ii) accelerated Minibatch SGD is optimal when the heterogeneity is high, and (iii) present the first upper bound for Local SGD that improves over Minibatch SGD in a non-homogeneous regime.
Is Local SGD Better than Minibatch SGD?
Feb 18, 2020
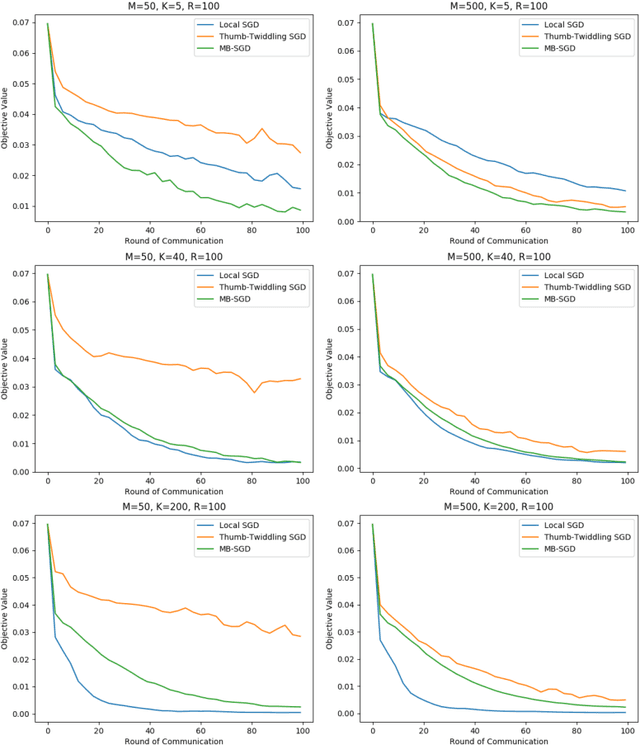

Abstract:We study local SGD (also known as parallel SGD and federated averaging), a natural and frequently used stochastic distributed optimization method. Its theoretical foundations are currently lacking and we highlight how all existing error guarantees in the convex setting are dominated by a simple baseline, minibatch SGD. (1) For quadratic objectives we prove that local SGD strictly dominates minibatch SGD and that accelerated local SGD is minimax optimal for quadratics; (2) For general convex objectives we provide the first guarantee that at least sometimes improves over minibatch SGD; (3) We show that indeed local SGD does not dominate minibatch SGD by presenting a lower bound on the performance of local SGD that is worse than the minibatch SGD guarantee.
Communication trade-offs for synchronized distributed SGD with large step size
Apr 25, 2019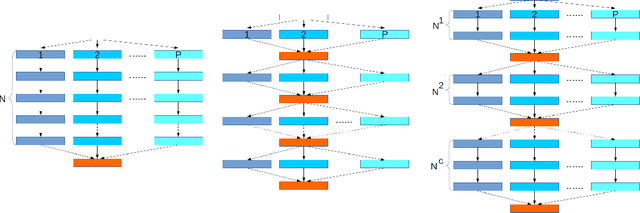

Abstract:Synchronous mini-batch SGD is state-of-the-art for large-scale distributed machine learning. However, in practice, its convergence is bottlenecked by slow communication rounds between worker nodes. A natural solution to reduce communication is to use the \emph{`local-SGD'} model in which the workers train their model independently and synchronize every once in a while. This algorithm improves the computation-communication trade-off but its convergence is not understood very well. We propose a non-asymptotic error analysis, which enables comparison to \emph{one-shot averaging} i.e., a single communication round among independent workers, and \emph{mini-batch averaging} i.e., communicating at every step. We also provide adaptive lower bounds on the communication frequency for large step-sizes ($ t^{-\alpha} $, $ \alpha\in (1/2 , 1 ) $) and show that \emph{Local-SGD} reduces communication by a factor of $O\Big(\frac{\sqrt{T}}{P^{3/2}}\Big)$, with $T$ the total number of gradients and $P$ machines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge