CLAW: Learning Continuous Latent Action World Models via Adversarial Latent Regularization

We introduce CLAW, a fully end-to-end self-supervised framework for learning a world model jointly with continuous latent action representations directly from action-free videos. Our approach leverages adversarial latent regularization and diffusion-based video generation to capture structured and semantically meaningful action representations while modeling rich, predictive environment dynamics, without relying on any action labels or annotations. By simultaneously training the Latent Action Model and world model, CLAW learns to reason about how inferred actions induce environment transitions from visual observations alone. We show that the resulting latent action world model supports both imitation learning from observation and goal-directed planning. In imitation learning, latent actions extracted from raw videos enable behavior cloning. For planning, CLAW generates sequences of latent actions and maps them to executable actions to reach desired goals. Extensive experiments across diverse tasks and embodiments demonstrate that CLAW produces semantically meaningful latent action representations, supports effective action transfer, and enables planning and imitation from observation, outperforming existing methods.

What Are We Actually Benchmarking in Robot Manipulation?

A robotics benchmark score measures success under one fixed evaluation setup, yet is routinely treated as evidence of general manipulation capability. We identify four failure modes, each of which weakens or invalidates a benchmark's role as a valid proxy for that capability: shortcut solvability, lack of statistical significance, creeping overfitting, and data-source dependence. We propose one diagnostic per failure mode. We audit LIBERO, CALVIN, SimplerEnv, RoboCasa, and RoboTwin 2.0 under these diagnostics. LIBERO and CALVIN fail multiple diagnostics. RoboCasa and RoboTwin 2.0 fail fewer, despite appearing far less often in recent progress claims. On LIBERO, a 0.09B probe with no language encoder scores at or near reported SOTA, and most reported gains are not provably statistically significant. On CALVIN, randomizing block poses within the training range drops performance for every tested policy. We release the four diagnostics with reference implementations for authors and reviewers to apply before treating a benchmark score as evidence of progress. Code and artifacts are available at https://ripl.github.io/manipulation_benchmark_audit/.

Approaching Deep Learning through the Spectral Dynamics of Weights

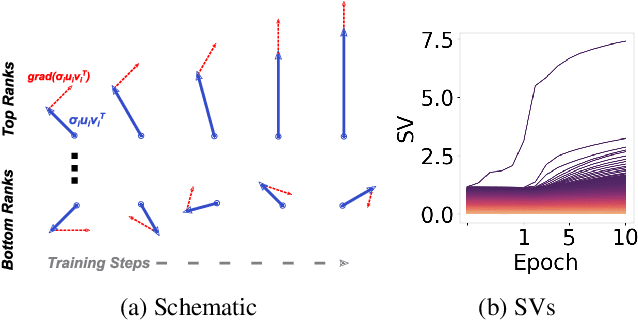
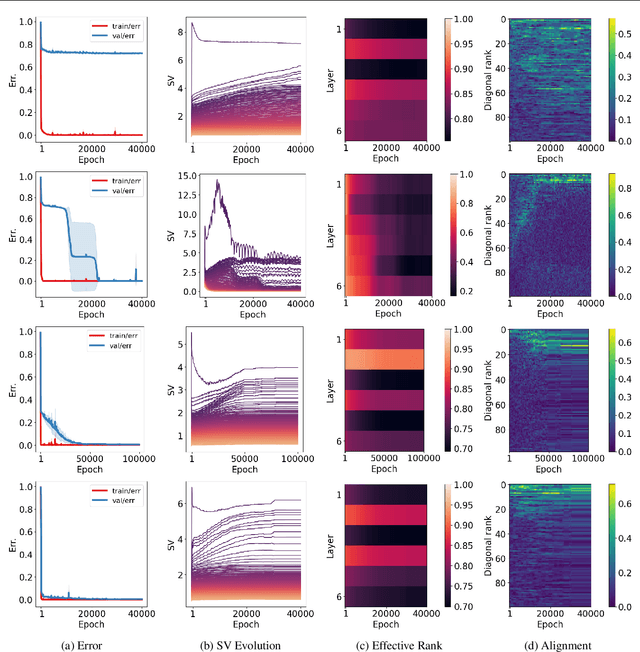
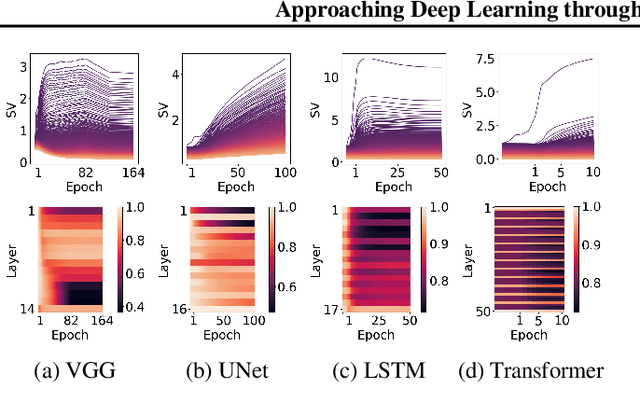
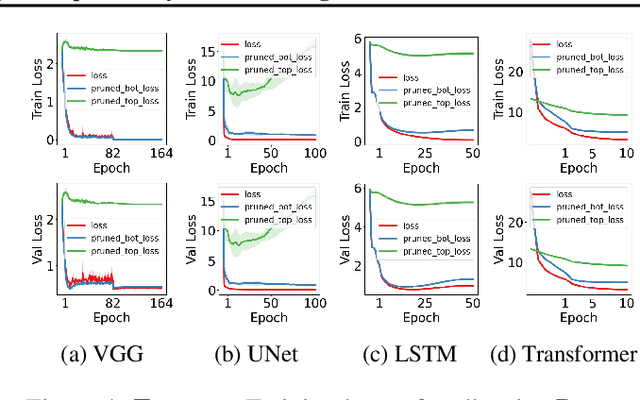
We propose an empirical approach centered on the spectral dynamics of weights -- the behavior of singular values and vectors during optimization -- to unify and clarify several phenomena in deep learning. We identify a consistent bias in optimization across various experiments, from small-scale ``grokking'' to large-scale tasks like image classification with ConvNets, image generation with UNets, speech recognition with LSTMs, and language modeling with Transformers. We also demonstrate that weight decay enhances this bias beyond its role as a norm regularizer, even in practical systems. Moreover, we show that these spectral dynamics distinguish memorizing networks from generalizing ones, offering a novel perspective on this longstanding conundrum. Additionally, we leverage spectral dynamics to explore the emergence of well-performing sparse subnetworks (lottery tickets) and the structure of the loss surface through linear mode connectivity. Our findings suggest that spectral dynamics provide a coherent framework to better understand the behavior of neural networks across diverse settings.