Approaching Deep Learning through the Spectral Dynamics of Weights

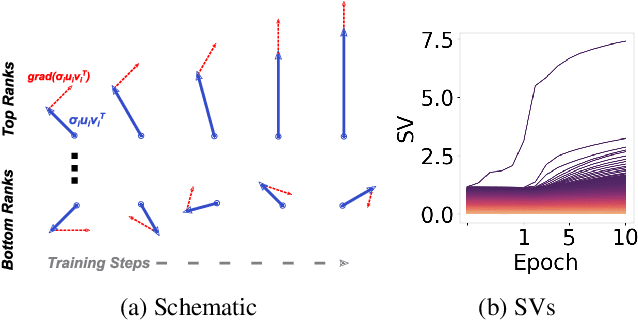
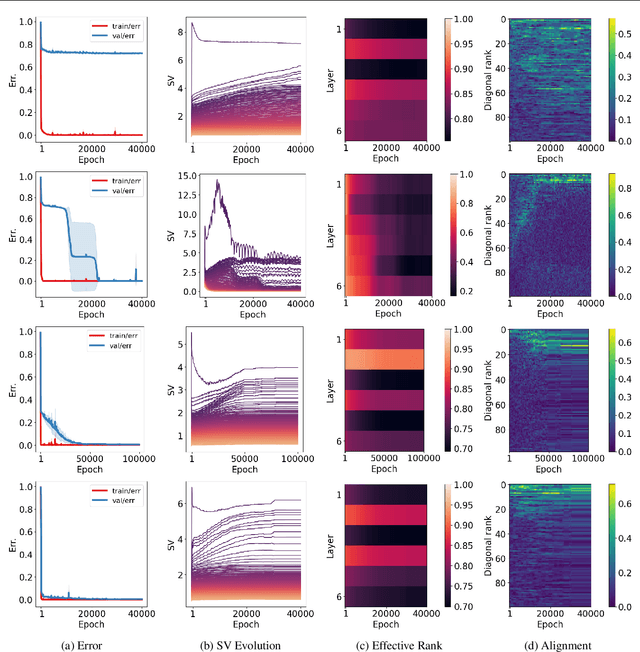
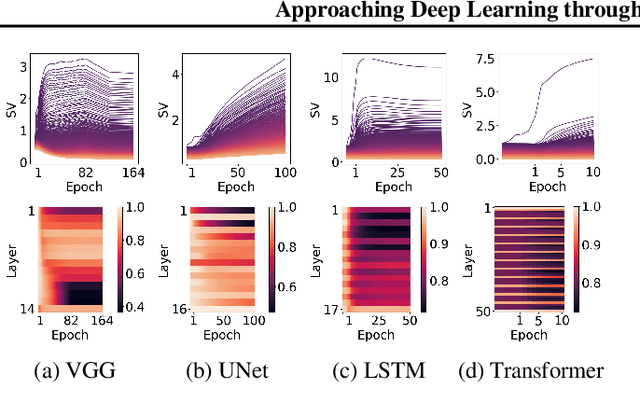
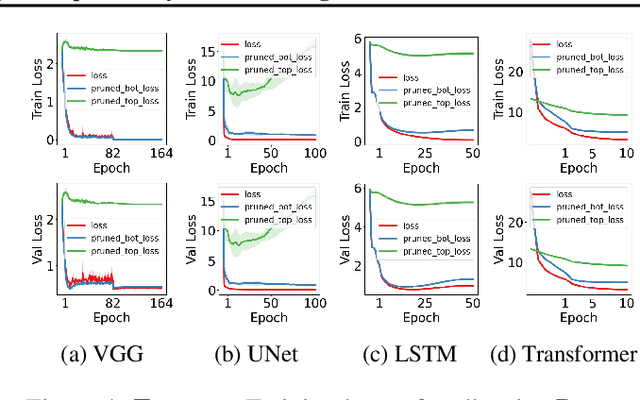
We propose an empirical approach centered on the spectral dynamics of weights -- the behavior of singular values and vectors during optimization -- to unify and clarify several phenomena in deep learning. We identify a consistent bias in optimization across various experiments, from small-scale ``grokking'' to large-scale tasks like image classification with ConvNets, image generation with UNets, speech recognition with LSTMs, and language modeling with Transformers. We also demonstrate that weight decay enhances this bias beyond its role as a norm regularizer, even in practical systems. Moreover, we show that these spectral dynamics distinguish memorizing networks from generalizing ones, offering a novel perspective on this longstanding conundrum. Additionally, we leverage spectral dynamics to explore the emergence of well-performing sparse subnetworks (lottery tickets) and the structure of the loss surface through linear mode connectivity. Our findings suggest that spectral dynamics provide a coherent framework to better understand the behavior of neural networks across diverse settings.

SySMOL: A Hardware-software Co-design Framework for Ultra-Low and Fine-Grained Mixed-Precision Neural Networks

Recent advancements in quantization and mixed-precision techniques offer significant promise for improving the run-time and energy efficiency of neural networks. In this work, we further showed that neural networks, wherein individual parameters or activations can take on different precisions ranging between 1 and 4 bits, can achieve accuracies comparable to or exceeding the full-precision counterparts. However, the deployment of such networks poses numerous challenges, stemming from the necessity to manage and control the compute/communication/storage requirements associated with these extremely fine-grained mixed precisions for each piece of data. There is a lack of existing efficient hardware and system-level support tailored to these unique and challenging requirements. Our research introduces the first novel holistic hardware-software co-design approach for these networks, which enables a continuous feedback loop between hardware design, training, and inference to facilitate systematic design exploration. As a proof-of-concept, we illustrate this co-design approach by designing new, configurable CPU SIMD architectures tailored for these networks, tightly integrating the architecture with new system-aware training and inference techniques. We perform systematic design space exploration using this framework to analyze various tradeoffs. The design for mixed-precision networks that achieves optimized tradeoffs corresponds to an architecture that supports 1, 2, and 4-bit fixed-point operations with four configurable precision patterns, when coupled with system-aware training and inference optimization -- networks trained for this design achieve accuracies that closely match full-precision accuracies, while compressing and improving run-time efficiency of the neural networks drastically by 10-20x, compared to full-precision networks.

Accelerated Training via Incrementally Growing Neural Networks using Variance Transfer and Learning Rate Adaptation

We develop an approach to efficiently grow neural networks, within which parameterization and optimization strategies are designed by considering their effects on the training dynamics. Unlike existing growing methods, which follow simple replication heuristics or utilize auxiliary gradient-based local optimization, we craft a parameterization scheme which dynamically stabilizes weight, activation, and gradient scaling as the architecture evolves, and maintains the inference functionality of the network. To address the optimization difficulty resulting from imbalanced training effort distributed to subnetworks fading in at different growth phases, we propose a learning rate adaption mechanism that rebalances the gradient contribution of these separate subcomponents. Experimental results show that our method achieves comparable or better accuracy than training large fixed-size models, while saving a substantial portion of the original computation budget for training. We demonstrate that these gains translate into real wall-clock training speedups.

Information-Theoretic Segmentation by Inpainting Error Maximization

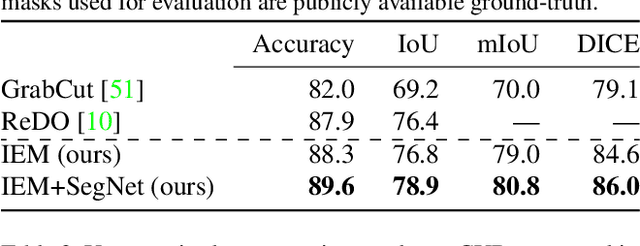
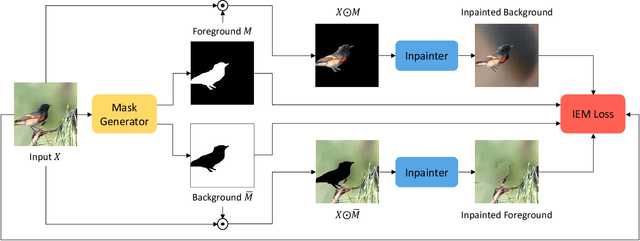
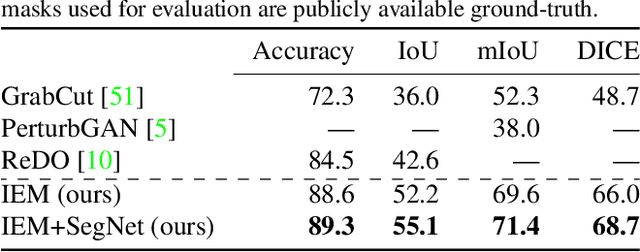
We study image segmentation from an information-theoretic perspective, proposing a novel adversarial method that performs unsupervised segmentation by partitioning images into maximally independent sets. More specifically, we group image pixels into foreground and background, with the goal of minimizing predictability of one set from the other. An easily computed loss drives a greedy search process to maximize inpainting error over these partitions. Our method does not involve training deep networks, is computationally cheap, class-agnostic, and even applicable in isolation to a single unlabeled image. Experiments demonstrate that it achieves a new state-of-the-art in unsupervised segmentation quality, while being substantially faster and more general than competing approaches.

Growing Efficient Deep Networks by Structured Continuous Sparsification

We develop an approach to training deep networks while dynamically adjusting their architecture, driven by a principled combination of accuracy and sparsity objectives. Unlike conventional pruning approaches, our method adopts a gradual continuous relaxation of discrete network structure optimization and then samples sparse subnetworks, enabling efficient deep networks to be trained in a growing and pruning manner. Extensive experiments across CIFAR-10, ImageNet, PASCAL VOC, and Penn Treebank, with convolutional models for image classification and semantic segmentation, and recurrent models for language modeling, show that our training scheme yields efficient networks that are smaller and more accurate than those produced by competing pruning methods.

Kernel and Rich Regimes in Overparametrized Models

A recent line of work studies overparametrized neural networks in the "kernel regime," i.e. when the network behaves during training as a kernelized linear predictor, and thus training with gradient descent has the effect of finding the minimum RKHS norm solution. This stands in contrast to other studies which demonstrate how gradient descent on overparametrized multilayer networks can induce rich implicit biases that are not RKHS norms. Building on an observation by Chizat and Bach, we show how the scale of the initialization controls the transition between the "kernel" (aka lazy) and "rich" (aka active) regimes and affects generalization properties in multilayer homogeneous models. We also highlight an interesting role for the width of a model in the case that the predictor is not identically zero at initialization. We provide a complete and detailed analysis for a family of simple depth-$D$ models that already exhibit an interesting and meaningful transition between the kernel and rich regimes, and we also demonstrate this transition empirically for more complex matrix factorization models and multilayer non-linear networks.

Domain-independent Dominance of Adaptive Methods

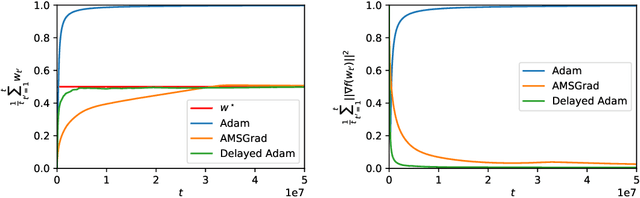
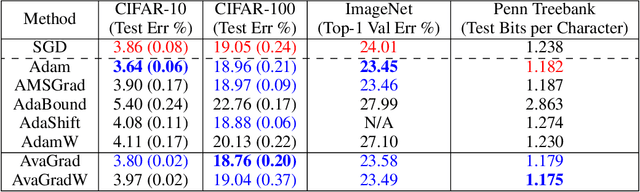
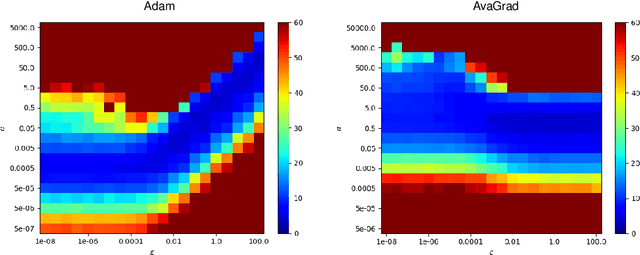
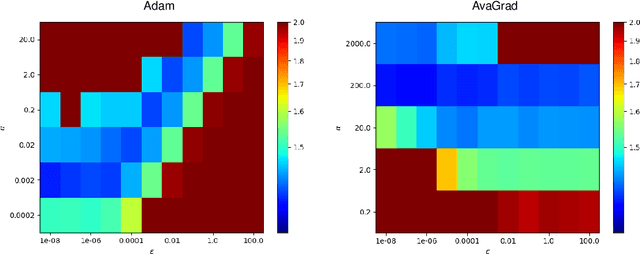
From a simplified analysis of adaptive methods, we derive AvaGrad, a new optimizer which outperforms SGD on vision tasks when its adaptability is properly tuned. We observe that the power of our method is partially explained by a decoupling of learning rate and adaptability, greatly simplifying hyperparameter search. In light of this observation, we demonstrate that, against conventional wisdom, Adam can also outperform SGD on vision tasks, as long as the coupling between its learning rate and adaptability is taken into account. In practice, AvaGrad matches the best results, as measured by generalization accuracy, delivered by any existing optimizer (SGD or adaptive) across image classification (CIFAR, ImageNet) and character-level language modelling (Penn Treebank) tasks. This later observation, alongside of AvaGrad's decoupling of hyperparameters, could make it the preferred optimizer for deep learning, replacing both SGD and Adam.

Winning the Lottery with Continuous Sparsification

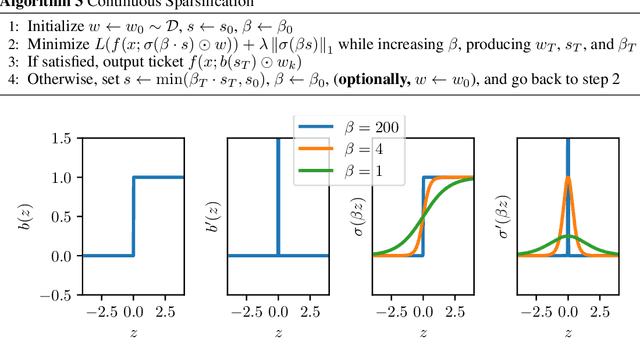
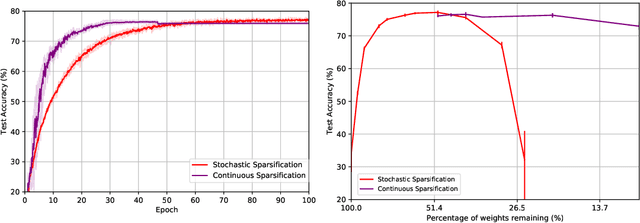
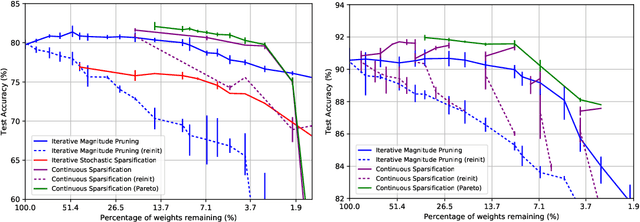
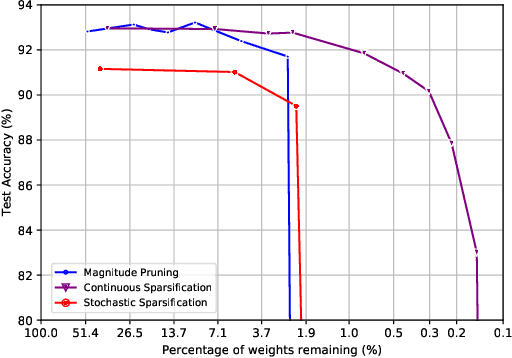
The Lottery Ticket Hypothesis from Frankle & Carbin (2019) conjectures that, for typically-sized neural networks, it is possible to find small sub-networks which train faster and yield superior performance than their original counterparts. The proposed algorithm to search for "winning tickets", Iterative Magnitude Pruning, consistently finds sub-networks with $90-95\%$ less parameters which train faster and better than the overparameterized models they were extracted from, creating potential applications to problems such as transfer learning. In this paper, we propose Continuous Sparsification, a new algorithm to search for winning tickets which continuously removes parameters from a network during training, and learns the sub-network's structure with gradient-based methods instead of relying on pruning strategies. We show empirically that our method is capable of finding tickets that outperforms the ones learned by Iterative Magnitude Pruning, and at the same time providing faster search, when measured in number of training epochs or wall-clock time.

Building a Massive Corpus for Named Entity Recognition using Free Open Data Sources

With the recent progress in machine learning, boosted by techniques such as deep learning, many tasks can be successfully solved once a large enough dataset is available for training. Nonetheless, human-annotated datasets are often expensive to produce, especially when labels are fine-grained, as is the case of Named Entity Recognition (NER), a task that operates with labels on a word-level. In this paper, we propose a method to automatically generate labeled datasets for NER from public data sources by exploiting links and structured data from DBpedia and Wikipedia. Due to the massive size of these data sources, the resulting dataset -- SESAME Available at https://sesame-pt.github.io -- is composed of millions of labeled sentences. We detail the method to generate the dataset, report relevant statistics, and design a baseline using a neural network, showing that our dataset helps building better NER predictors.

On the Convergence of AdaBound and its Connection to SGD

Adaptive gradient methods such as Adam have gained extreme popularity due to their success in training complex neural networks and less sensitivity to hyperparameter tuning compared to SGD. However, it has been recently shown that Adam can fail to converge and might cause poor generalization -- this lead to the design of new, sophisticated adaptive methods which attempt to generalize well while being theoretically reliable. In this technical report we focus on AdaBound, a promising, recently proposed optimizer. We present a stochastic convex problem for which AdaBound can provably take arbitrarily long to converge in terms of a factor which is not accounted for in the convergence rate guarantee of Luo et al. (2019). We present a new $O(\sqrt T)$ regret guarantee under different assumptions on the bound functions, and provide empirical results on CIFAR suggesting that a specific form of momentum SGD can match AdaBound's performance while having less hyperparameters and lower computational costs.