Context-Efficient Retrieval with Factual Decomposition

There has recently been considerable interest in incorporating information retrieval into large language models (LLMs). Retrieval from a dynamically expanding external corpus of text allows a model to incorporate current events and can be viewed as a form of episodic memory. Here we demonstrate that pre-processing the external corpus into semi-structured ''atomic facts'' makes retrieval more efficient. More specifically, we demonstrate that our particular form of atomic facts improves performance on various question answering tasks when the amount of retrieved text is limited. Limiting the amount of retrieval reduces the size of the context and improves inference efficiency.

PENCIL: Long Thoughts with Short Memory

While recent works (e.g. o1, DeepSeek R1) have demonstrated great promise of using long Chain-of-Thought (CoT) to improve reasoning capabilities of language models, scaling it up during test-time is challenging due to inefficient memory usage -- intermediate computations accumulate indefinitely in context even no longer needed for future thoughts. We propose PENCIL, which incorporates a reduction mechanism into the autoregressive generation process, allowing the model to recursively clean up intermediate thoughts based on patterns learned from training. With this reduction mechanism, PENCIL significantly reduces the maximal context length required during generation, and thus can generate longer thoughts with limited memory, solving larger-scale problems given more thinking time. For example, we demonstrate PENCIL achieves 97\% accuracy on the challenging Einstein's puzzle -- a task even large models like GPT-4 struggle with -- using only a small 25M-parameter transformer with 2048 context length. Theoretically, we prove PENCIL can perform universal space-efficient computation by simulating Turing machines with optimal time and space complexity, and thus can solve arbitrary computational tasks that would otherwise be intractable given context window constraints.

On the Mathematics of Diffusion Models

This paper attempts to present the stochastic differential equations of diffusion models in a manner that is accessible to a broad audience. The diffusion process is defined over a population density in R^d. Of particular interest is a population of images. In a diffusion model one first defines a diffusion process that takes a sample from the population and gradually adds noise until only noise remains. The fundamental idea is to sample from the population by a reverse-diffusion process mapping pure noise to a population sample. The diffusion process is defined independent of any ``interpretation'' but can be analyzed using the mathematics of variational auto-encoders (the ``VAE interpretation'') or the Fokker-Planck equation (the ``score-matching intgerpretation''). Both analyses yield reverse-diffusion methods involving the score function. The Fokker-Planck analysis yields a family of reverse-diffusion SDEs parameterized by any desired level of reverse-diffusion noise including zero (deterministic reverse-diffusion). The VAE analysis yields the reverse-diffusion SDE at the same noise level as the diffusion SDE. The VAE analysis also yields a useful expression for computing the population probabilities of a given point (image). This formula for the probability of a given point does not seem to follow naturally from the Fokker-Planck analysis. Much, but apparently not all, of the mathematics presented here can be found in the literature. Attributions are given at the end of the paper.

Information-Theoretic Segmentation by Inpainting Error Maximization

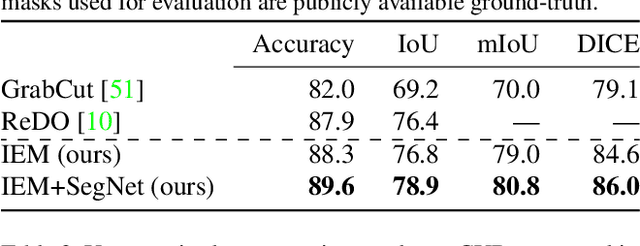
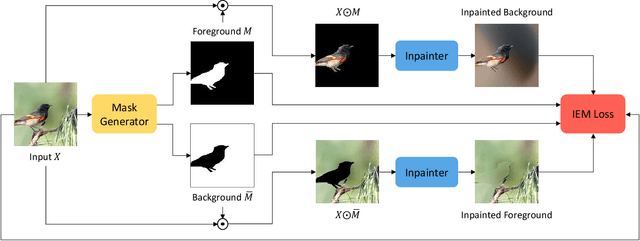
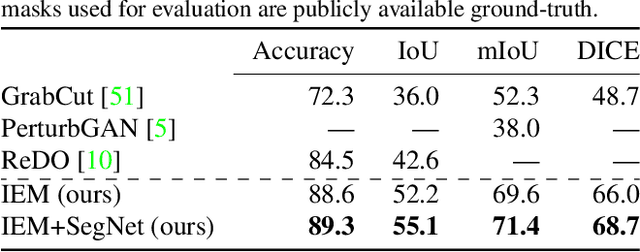
We study image segmentation from an information-theoretic perspective, proposing a novel adversarial method that performs unsupervised segmentation by partitioning images into maximally independent sets. More specifically, we group image pixels into foreground and background, with the goal of minimizing predictability of one set from the other. An easily computed loss drives a greedy search process to maximize inpainting error over these partitions. Our method does not involve training deep networks, is computationally cheap, class-agnostic, and even applicable in isolation to a single unlabeled image. Experiments demonstrate that it achieves a new state-of-the-art in unsupervised segmentation quality, while being substantially faster and more general than competing approaches.

On-The-Fly Information Retrieval Augmentation for Language Models

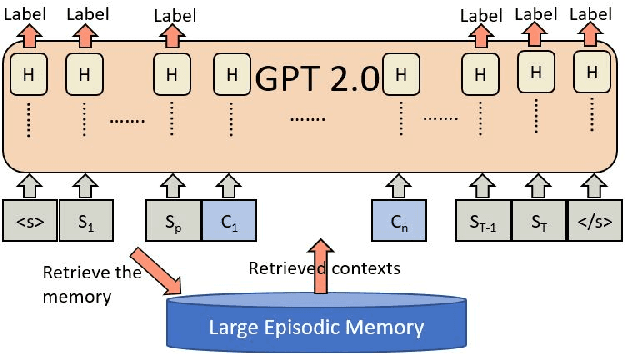
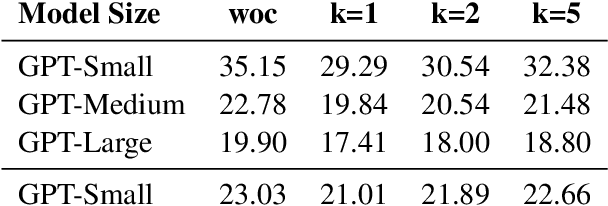
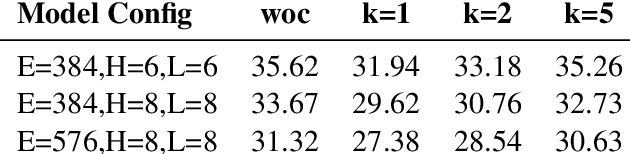
Here we experiment with the use of information retrieval as an augmentation for pre-trained language models. The text corpus used in information retrieval can be viewed as form of episodic memory which grows over time. By augmenting GPT 2.0 with information retrieval we achieve a zero shot 15% relative reduction in perplexity on Gigaword corpus without any re-training. We also validate our IR augmentation on an event co-reference task.

MathZero, The Classification Problem, and Set-Theoretic Type Theory

AlphaZero learns to play go, chess and shogi at a superhuman level through self play given only the rules of the game. This raises the question of whether a similar thing could be done for mathematics -- a MathZero. MathZero would require a formal foundation and an objective. We propose the foundation of set-theoretic dependent type theory and an objective defined in terms of the classification problem -- the problem of classifying concept instances up to isomorphism. The natural numbers arise as the solution to the classification problem for finite sets. Here we generalize classical Bourbaki set-theoretic isomorphism to set-theoretic dependent type theory. To our knowledge we give the first isomorphism inference rules for set-theoretic dependent type theory with propositional set-theoretic equality. The presentation is intended to be accessible to mathematicians with no prior exposure to type theory.

Domain-independent Dominance of Adaptive Methods

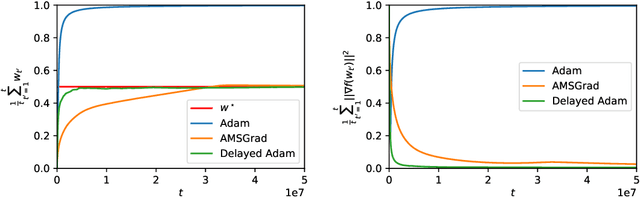
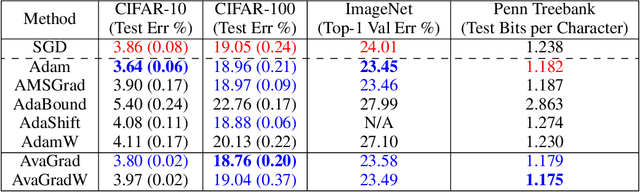
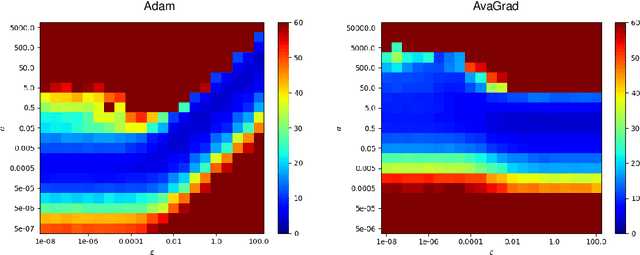
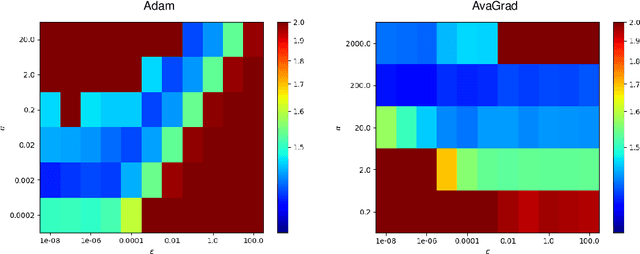
From a simplified analysis of adaptive methods, we derive AvaGrad, a new optimizer which outperforms SGD on vision tasks when its adaptability is properly tuned. We observe that the power of our method is partially explained by a decoupling of learning rate and adaptability, greatly simplifying hyperparameter search. In light of this observation, we demonstrate that, against conventional wisdom, Adam can also outperform SGD on vision tasks, as long as the coupling between its learning rate and adaptability is taken into account. In practice, AvaGrad matches the best results, as measured by generalization accuracy, delivered by any existing optimizer (SGD or adaptive) across image classification (CIFAR, ImageNet) and character-level language modelling (Penn Treebank) tasks. This later observation, alongside of AvaGrad's decoupling of hyperparameters, could make it the preferred optimizer for deep learning, replacing both SGD and Adam.

Evidence Sentence Extraction for Machine Reading Comprehension

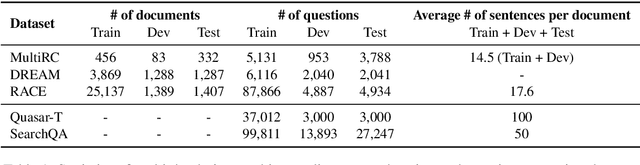
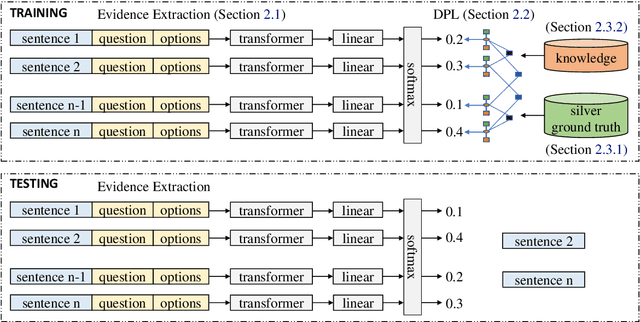
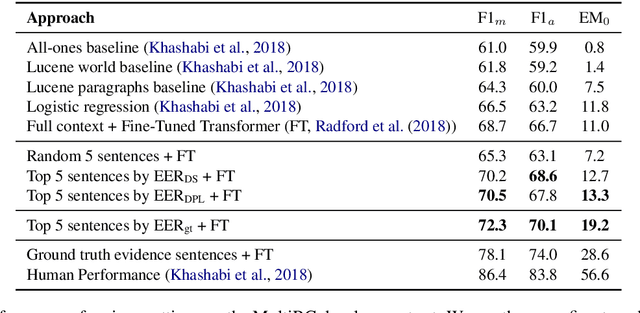
Recently remarkable success has been achieved in machine reading comprehension (MRC). However, it is still difficult to interpret the predictions of existing MRC models. In this paper, we focus on: extracting evidence sentences that can explain/support answer predictions for multiple-choice MRC tasks, where the majority of answer options cannot be directly extracted from reference documents; studying the impacts of using the extracted sentences as the input of MRC models. Due to the lack of ground truth evidence sentence labels in most cases, we apply distant supervision to generate imperfect labels and then use them to train a neural evidence extractor. To denoise the noisy labels, we treat labels as latent variables and define priors over these latent variables by incorporating rich linguistic knowledge under a recently proposed deep probabilistic logic learning framework. We feed the extracted evidence sentences into existing MRC models and evaluate the end-to-end performance on three challenging multiple-choice MRC datasets: MultiRC, DREAM, and RACE, achieving comparable or better performance than the same models that take the full context as input. Our evidence extractor also outperforms a state-of-the-art sentence selector by a large margin on two open-domain question answering datasets: Quasar-T and SearchQA. To the best of our knowledge, this is the first work addressing evidence sentence extraction for multiple-choice MRC.

Formal Limitations on the Measurement of Mutual Information

Motivate by applications to unsupervised learning, we consider the problem of measuring mutual information. Recent analysis has shown that naive kNN estimators of mutual information have serious statistical limitations motivating more refined methods. In this paper we prove that serious statistical limitations are inherent to any measurement method. More specifically, we show that any distribution-free high-confidence lower bound on mutual information cannot be larger than $O(\ln N)$ where $N$ is the size of the data sample. We also analyze the Donsker-Varadhan lower bound on KL divergence in particular and show that, when simple statistical considerations are taken into account, this bound can never produce a high-confidence value larger than $\ln N$. While large high-confidence lower bounds are impossible, in practice one can use estimators without formal guarantees. We suggest expressing mutual information as a difference of entropies and using cross-entropy as an entropy estimator. We observe that, although cross-entropy is only an upper bound on entropy, cross-entropy estimates converge to the true cross-entropy at the rate of $1/\sqrt{N}$.

Information Theoretic Co-Training

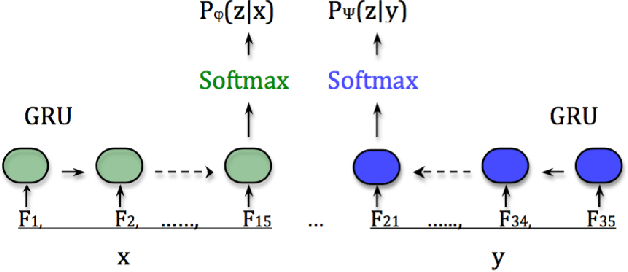
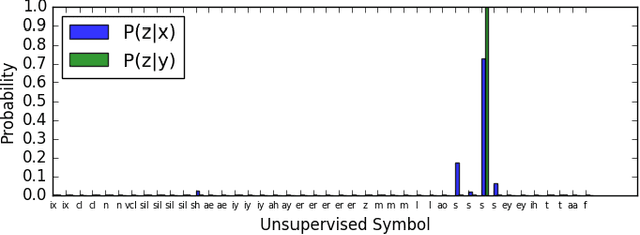
This paper introduces an information theoretic co-training objective for unsupervised learning. We consider the problem of predicting the future. Rather than predict future sensations (image pixels or sound waves) we predict "hypotheses" to be confirmed by future sensations. More formally, we assume a population distribution on pairs $(x,y)$ where we can think of $x$ as a past sensation and $y$ as a future sensation. We train both a predictor model $P_\Phi(z|x)$ and a confirmation model $P_\Psi(z|y)$ where we view $z$ as hypotheses (when predicted) or facts (when confirmed). For a population distribution on pairs $(x,y)$ we focus on the problem of measuring the mutual information between $x$ and $y$. By the data processing inequality this mutual information is at least as large as the mutual information between $x$ and $z$ under the distribution on triples $(x,z,y)$ defined by the confirmation model $P_\Psi(z|y)$. The information theoretic training objective for $P_\Phi(z|x)$ and $P_\Psi(z|y)$ can be viewed as a form of co-training where we want the prediction from $x$ to match the confirmation from $y$.