Winning the Lottery with Continuous Sparsification
Paper and Code
Dec 10, 2019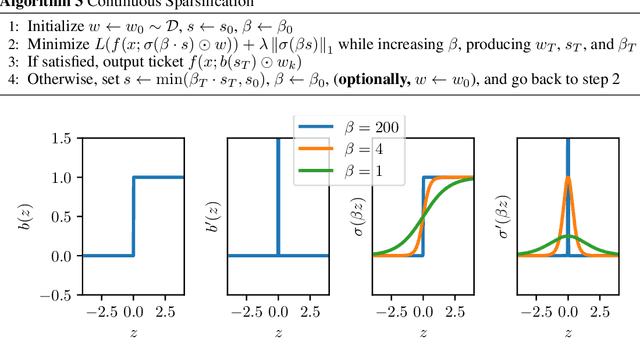
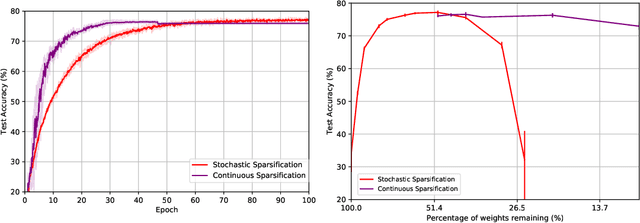
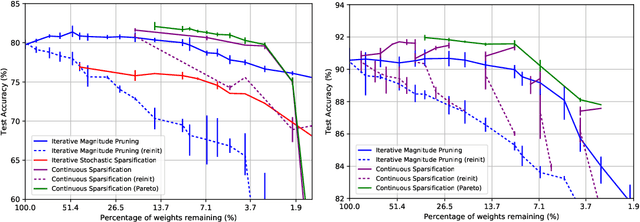
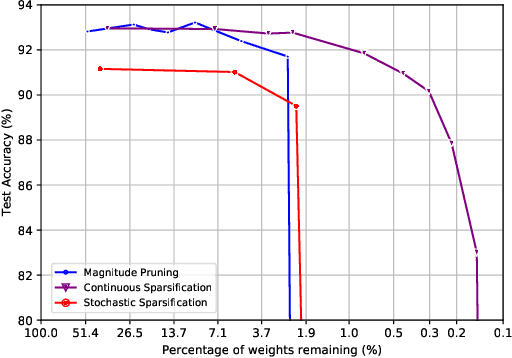
The Lottery Ticket Hypothesis from Frankle & Carbin (2019) conjectures that, for typically-sized neural networks, it is possible to find small sub-networks which train faster and yield superior performance than their original counterparts. The proposed algorithm to search for "winning tickets", Iterative Magnitude Pruning, consistently finds sub-networks with $90-95\%$ less parameters which train faster and better than the overparameterized models they were extracted from, creating potential applications to problems such as transfer learning. In this paper, we propose Continuous Sparsification, a new algorithm to search for winning tickets which continuously removes parameters from a network during training, and learns the sub-network's structure with gradient-based methods instead of relying on pruning strategies. We show empirically that our method is capable of finding tickets that outperforms the ones learned by Iterative Magnitude Pruning, and at the same time providing faster search, when measured in number of training epochs or wall-clock time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge