Continual Learning in Linear Classification on Separable Data

We analyze continual learning on a sequence of separable linear classification tasks with binary labels. We show theoretically that learning with weak regularization reduces to solving a sequential max-margin problem, corresponding to a special case of the Projection Onto Convex Sets (POCS) framework. We then develop upper bounds on the forgetting and other quantities of interest under various settings with recurring tasks, including cyclic and random orderings of tasks. We discuss several practical implications to popular training practices like regularization scheduling and weighting. We point out several theoretical differences between our continual classification setting and a recently studied continual regression setting.

How catastrophic can catastrophic forgetting be in linear regression?

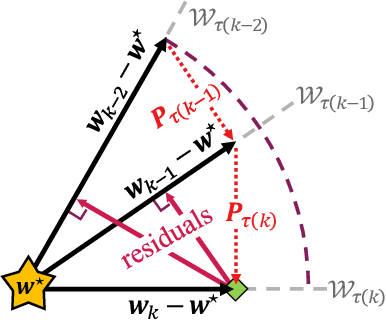
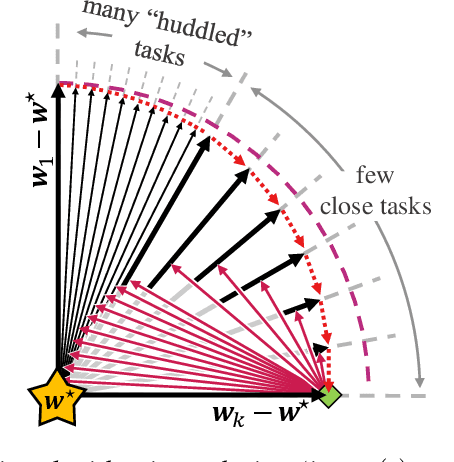
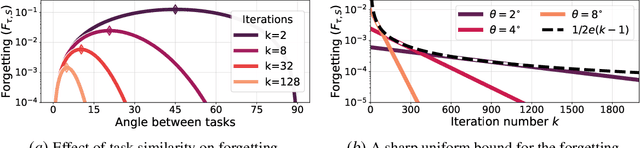
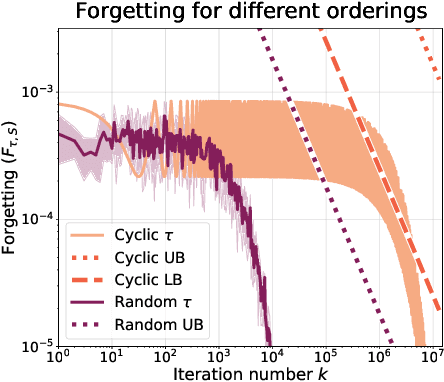
To better understand catastrophic forgetting, we study fitting an overparameterized linear model to a sequence of tasks with different input distributions. We analyze how much the model forgets the true labels of earlier tasks after training on subsequent tasks, obtaining exact expressions and bounds. We establish connections between continual learning in the linear setting and two other research areas: alternating projections and the Kaczmarz method. In specific settings, we highlight differences between forgetting and convergence to the offline solution as studied in those areas. In particular, when T tasks in d dimensions are presented cyclically for k iterations, we prove an upper bound of T^2 * min{1/sqrt(k), d/k} on the forgetting. This stands in contrast to the convergence to the offline solution, which can be arbitrarily slow according to existing alternating projection results. We further show that the T^2 factor can be lifted when tasks are presented in a random ordering.

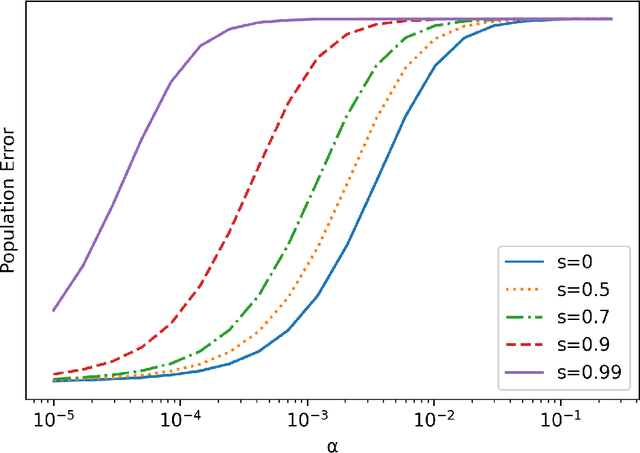
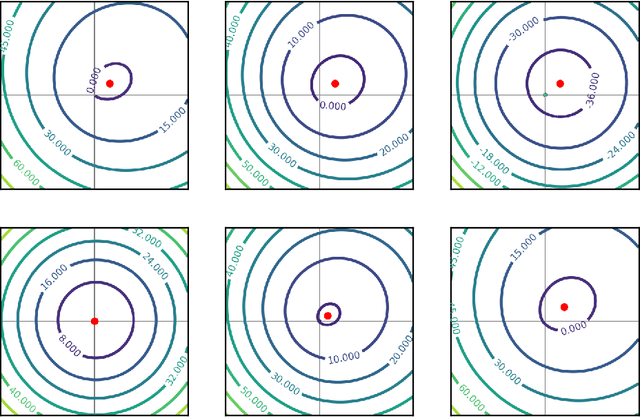
On the Implicit Bias of Initialization Shape: Beyond Infinitesimal Mirror Descent

Recent work has highlighted the role of initialization scale in determining the structure of the solutions that gradient methods converge to. In particular, it was shown that large initialization leads to the neural tangent kernel regime solution, whereas small initialization leads to so called "rich regimes". However, the initialization structure is richer than the overall scale alone and involves relative magnitudes of different weights and layers in the network. Here we show that these relative scales, which we refer to as initialization shape, play an important role in determining the learned model. We develop a novel technique for deriving the inductive bias of gradient-flow and use it to obtain closed-form implicit regularizers for multiple cases of interest.

Implicit Bias in Deep Linear Classification: Initialization Scale vs Training Accuracy

We provide a detailed asymptotic study of gradient flow trajectories and their implicit optimization bias when minimizing the exponential loss over "diagonal linear networks". This is the simplest model displaying a transition between "kernel" and non-kernel ("rich" or "active") regimes. We show how the transition is controlled by the relationship between the initialization scale and how accurately we minimize the training loss. Our results indicate that some limit behaviors of gradient descent only kick in at ridiculous training accuracies (well beyond $10^{-100}$). Moreover, the implicit bias at reasonable initialization scales and training accuracies is more complex and not captured by these limits.

Kernel and Rich Regimes in Overparametrized Models

A recent line of work studies overparametrized neural networks in the "kernel regime," i.e. when the network behaves during training as a kernelized linear predictor, and thus training with gradient descent has the effect of finding the minimum RKHS norm solution. This stands in contrast to other studies which demonstrate how gradient descent on overparametrized multilayer networks can induce rich implicit biases that are not RKHS norms. Building on an observation by Chizat and Bach, we show how the scale of the initialization controls the transition between the "kernel" (aka lazy) and "rich" (aka active) regimes and affects generalization properties in multilayer homogeneous models. We also highlight an interesting role for the width of a model in the case that the predictor is not identically zero at initialization. We provide a complete and detailed analysis for a family of simple depth-$D$ models that already exhibit an interesting and meaningful transition between the kernel and rich regimes, and we also demonstrate this transition empirically for more complex matrix factorization models and multilayer non-linear networks.

Variance Estimation For Online Regression via Spectrum Thresholding

We consider the online linear regression problem, where the predictor vector may vary with time. This problem can be modelled as a linear dynamical system, where the parameters that need to be learned are the variance of both the process noise and the observation noise. The classical approach to learning the variance is via the maximum likelihood estimator -- a non-convex optimization problem prone to local minima and with no finite sample complexity bounds. In this paper we study the global system operator: the operator that maps the noises vectors to the output. In particular, we obtain estimates on its spectrum, and as a result derive the first known variance estimators with sample complexity guarantees for online regression problems. We demonstrate the approach on a number of synthetic and real-world benchmarks.

An Editorial Network for Enhanced Document Summarization

We suggest a new idea of Editorial Network - a mixed extractive-abstractive summarization approach, which is applied as a post-processing step over a given sequence of extracted sentences. Our network tries to imitate the decision process of a human editor during summarization. Within such a process, each extracted sentence may be either kept untouched, rephrased or completely rejected. We further suggest an effective way for training the "editor" based on a novel soft-labeling approach. Using the CNN/DailyMail dataset we demonstrate the effectiveness of our approach compared to state-of-the-art extractive-only or abstractive-only baseline methods.

Multi Instance Learning For Unbalanced Data

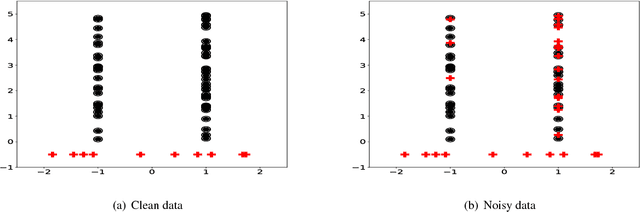
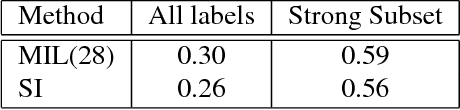
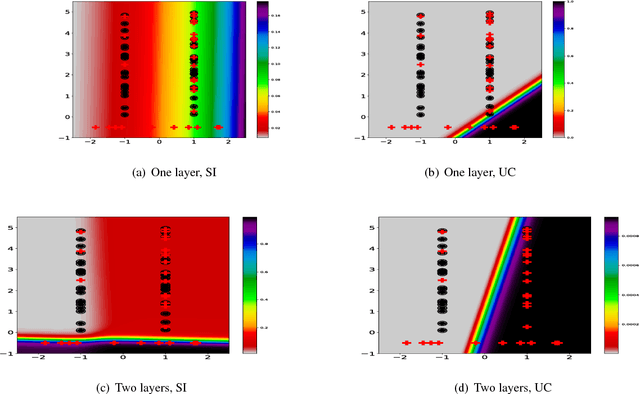
In the context of Multi Instance Learning, we analyze the Single Instance (SI) learning objective. We show that when the data is unbalanced and the family of classifiers is sufficiently rich, the SI method is a useful learning algorithm. In particular, we show that larger data imbalance, a quality that is typically perceived as negative, in fact implies a better resilience of the algorithm to the statistical dependencies of the objects in bags. In addition, our results shed new light on some known issues with the SI method in the setting of linear classifiers, and we show that these issues are significantly less likely to occur in the setting of neural networks. We demonstrate our results on a synthetic dataset, and on the COCO dataset for the problem of patch classification with weak image level labels derived from captions.

Efficient Loss-Based Decoding On Graphs For Extreme Classification

In extreme classification problems, learning algorithms are required to map instances to labels from an extremely large label set. We build on a recent extreme classification framework with logarithmic time and space, and on a general approach for error correcting output coding (ECOC), and introduce a flexible and efficient approach accompanied by bounds. Our framework employs output codes induced by graphs, and offers a tradeoff between accuracy and model size. We show how to find the sweet spot of this tradeoff using only the training data. Our experimental study demonstrates the validity of our assumptions and claims, and shows the superiority of our method compared with state-of-the-art algorithms.

Selective Sampling with Drift

Recently there has been much work on selective sampling, an online active learning setting, in which algorithms work in rounds. On each round an algorithm receives an input and makes a prediction. Then, it can decide whether to query a label, and if so to update its model, otherwise the input is discarded. Most of this work is focused on the stationary case, where it is assumed that there is a fixed target model, and the performance of the algorithm is compared to a fixed model. However, in many real-world applications, such as spam prediction, the best target function may drift over time, or have shifts from time to time. We develop a novel selective sampling algorithm for the drifting setting, analyze it under no assumptions on the mechanism generating the sequence of instances, and derive new mistake bounds that depend on the amount of drift in the problem. Simulations on synthetic and real-world datasets demonstrate the superiority of our algorithms as a selective sampling algorithm in the drifting setting.