Efficient Fairness-Performance Pareto Front Computation

There is a well known intrinsic trade-off between the fairness of a representation and the performance of classifiers derived from the representation. Due to the complexity of optimisation algorithms in most modern representation learning approaches, for a given method it may be non-trivial to decide whether the obtained fairness-performance curve of the method is optimal, i.e., whether it is close to the true Pareto front for these quantities for the underlying data distribution. In this paper we propose a new method to compute the optimal Pareto front, which does not require the training of complex representation models. We show that optimal fair representations possess several useful structural properties, and that these properties enable a reduction of the computation of the Pareto Front to a compact discrete problem. We then also show that these compact approximating problems can be efficiently solved via off-the shelf concave-convex programming methods. Since our approach is independent of the specific model of representations, it may be used as the benchmark to which representation learning algorithms may be compared. We experimentally evaluate the approach on a number of real world benchmark datasets.

Implicitly Normalized Explicitly Regularized Density Estimation

We propose a new approach to non-parametric density estimation, that is based on regularizing a Sobolev norm of the density. This method is provably different from Kernel Density Estimation, and makes the bias of the model clear and interpretable. While there is no closed analytic form for the associated kernel, we show that one can approximate it using sampling. The optimization problem needed to determine the density is non-convex, and standard gradient methods do not perform well. However, we show that with an appropriate initialization and using natural gradients, one can obtain well performing solutions. Finally, while the approach provides unnormalized densities, which prevents the use of log-likelihood for cross validation, we show that one can instead adapt Fisher Divergence based Score Matching methods for this task. We evaluate the resulting method on the comprehensive recent Anomaly Detection benchmark suite, ADBench, and find that it ranks second best, among more than 15 algorithms.

Whats Missing? Learning Hidden Markov Models When the Locations of Missing Observations are Unknown

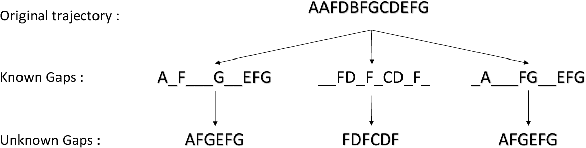
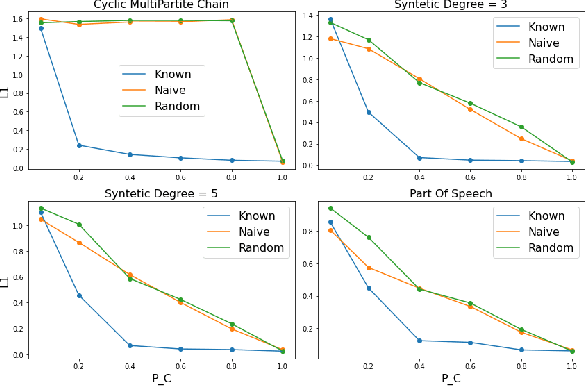
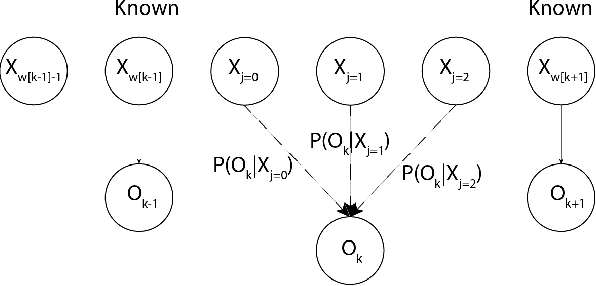
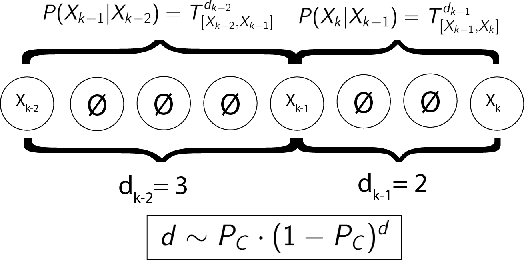
The Hidden Markov Model (HMM) is one of the most widely used statistical models for sequential data analysis, and it has been successfully applied in a large variety of domains. One of the key reasons for this versatility is the ability of HMMs to deal with missing data. However, standard HMM learning algorithms rely crucially on the assumption that the positions of the missing observations within the observation sequence are known. In some situations where such assumptions are not feasible, a number of special algorithms have been developed. Currently, these algorithms rely strongly on specific structural assumptions of the underlying chain, such as acyclicity, and are not applicable in the general case. In particular, there are numerous domains within medicine and computational biology, where the missing observation locations are unknown and acyclicity assumptions do not hold, thus presenting a barrier for the application of HMMs in those fields. In this paper we consider a general problem of learning HMMs from data with unknown missing observation locations (i.e., only the order of the non-missing observations are known). We introduce a generative model of the location omissions and propose two learning methods for this model, a (semi) analytic approach, and a Gibbs sampler. We evaluate and compare the algorithms in a variety of scenarios, measuring their reconstruction precision and robustness under model misspecification.

Dimension Free Generalization Bounds for Non Linear Metric Learning

In this work we study generalization guarantees for the metric learning problem, where the metric is induced by a neural network type embedding of the data. Specifically, we provide uniform generalization bounds for two regimes -- the sparse regime, and a non-sparse regime which we term \emph{bounded amplification}. The sparse regime bounds correspond to situations where $\ell_1$-type norms of the parameters are small. Similarly to the situation in classification, solutions satisfying such bounds can be obtained by an appropriate regularization of the problem. On the other hand, unregularized SGD optimization of a metric learning loss typically does not produce sparse solutions. We show that despite this lack of sparsity, by relying on a different, new property of the solutions, it is still possible to provide dimension free generalization guarantees. Consequently, these bounds can explain generalization in non sparse real experimental situations. We illustrate the studied phenomena on the MNIST and 20newsgroups datasets.

Topic Modeling via Full Dependence Mixtures

We consider the topic modeling problem for large datasets. For this problem, Latent Dirichlet Allocation (LDA) with a collapsed Gibbs sampler optimization is the state-of-the-art approach in terms of topic quality. However, LDA is a slow approach, and running it on large datasets is impractical even with modern hardware. In this paper we propose to fit topics directly to the co-occurances data of the corpus. In particular, we introduce an extension of a mixture model, the Full Dependence Mixture (FDM), which arises naturally as a model of a second moment under general generative assumptions on the data. While there is some previous work on topic modeling using second moments, we develop a direct stochastic optimization procedure for fitting an FDM with a single Kullback Leibler objective. While moment methods in general have the benefit that an iteration no longer needs to scale with the size of the corpus, our approach also allows us to leverage standard optimizers and GPUs for the problem of topic modeling. We evaluate the approach on synthetic and semi-synthetic data, as well as on the SOTU and Neurips Papers corpora, and show that the approach outperforms LDA, where LDA is run on both full and sub-sampled data.

Variance Estimation For Online Regression via Spectrum Thresholding

We consider the online linear regression problem, where the predictor vector may vary with time. This problem can be modelled as a linear dynamical system, where the parameters that need to be learned are the variance of both the process noise and the observation noise. The classical approach to learning the variance is via the maximum likelihood estimator -- a non-convex optimization problem prone to local minima and with no finite sample complexity bounds. In this paper we study the global system operator: the operator that maps the noises vectors to the output. In particular, we obtain estimates on its spectrum, and as a result derive the first known variance estimators with sample complexity guarantees for online regression problems. We demonstrate the approach on a number of synthetic and real-world benchmarks.

Multi Instance Learning For Unbalanced Data

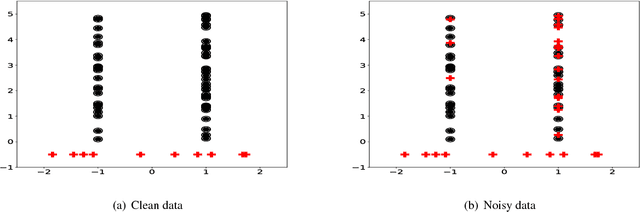
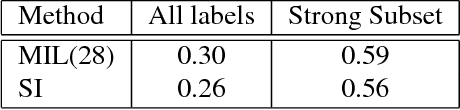
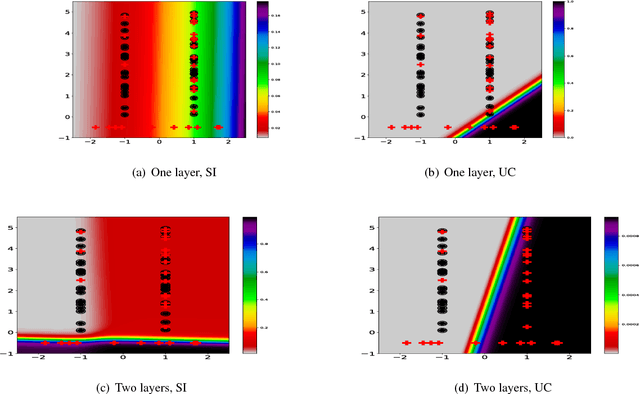
In the context of Multi Instance Learning, we analyze the Single Instance (SI) learning objective. We show that when the data is unbalanced and the family of classifiers is sufficiently rich, the SI method is a useful learning algorithm. In particular, we show that larger data imbalance, a quality that is typically perceived as negative, in fact implies a better resilience of the algorithm to the statistical dependencies of the objects in bags. In addition, our results shed new light on some known issues with the SI method in the setting of linear classifiers, and we show that these issues are significantly less likely to occur in the setting of neural networks. We demonstrate our results on a synthetic dataset, and on the COCO dataset for the problem of patch classification with weak image level labels derived from captions.

On-Line Learning of Linear Dynamical Systems: Exponential Forgetting in Kalman Filters

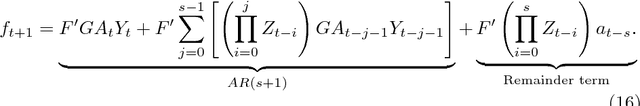
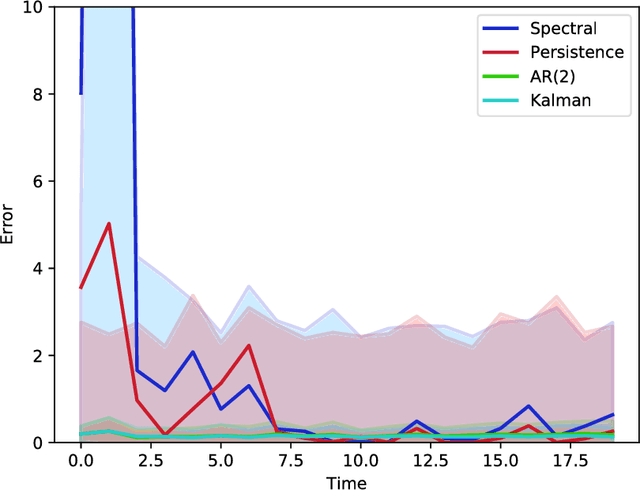
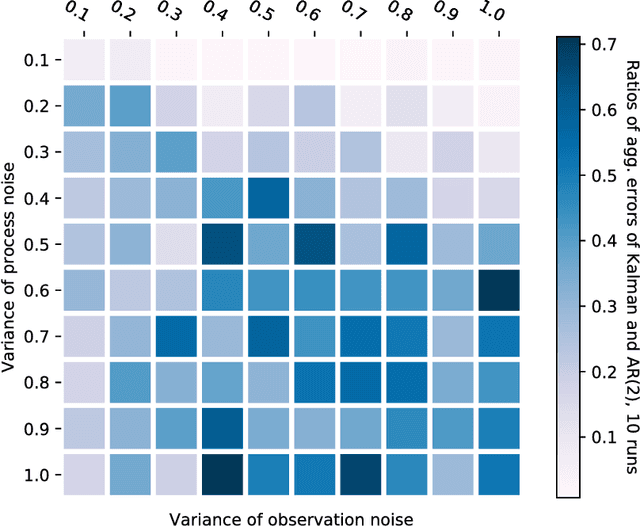
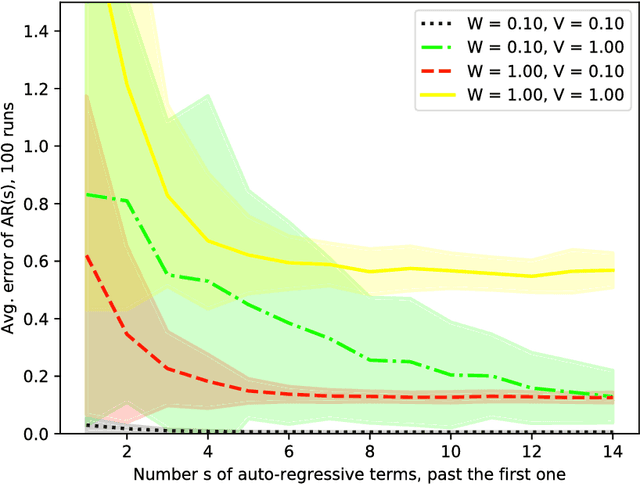
Kalman filter is a key tool for time-series forecasting and analysis. We show that the dependence of a prediction of Kalman filter on the past is decaying exponentially, whenever the process noise is non-degenerate. Therefore, Kalman filter may be approximated by regression on a few recent observations. Surprisingly, we also show that having some process noise is essential for the exponential decay. With no process noise, it may happen that the forecast depends on all of the past uniformly, which makes forecasting more difficult. Based on this insight, we devise an on-line algorithm for improper learning of a linear dynamical system (LDS), which considers only a few most recent observations. We use our decay results to provide the first regret bounds w.r.t. to Kalman filters within learning an LDS. That is, we compare the results of our algorithm to the best, in hindsight, Kalman filter for a given signal. Also, the algorithm is practical: its per-update run-time is linear in the regression depth.

Interdependent Gibbs Samplers

Gibbs sampling, as a model learning method, is known to produce the most accurate results available in a variety of domains, and is a de facto standard in these domains. Yet, it is also well known that Gibbs random walks usually have bottlenecks, sometimes termed "local maxima", and thus samplers often return suboptimal solutions. In this paper we introduce a variation of the Gibbs sampler which yields high likelihood solutions significantly more often than the regular Gibbs sampler. Specifically, we show that combining multiple samplers, with certain dependence (coupling) between them, results in higher likelihood solutions. This side-steps the well known issue of identifiability, which has been the obstacle to combining samplers in previous work. We evaluate the approach on a Latent Dirichlet Allocation model, and also on HMM's, where precise computation of likelihoods and comparisons to the standard EM algorithm are possible.

Clustering Time Series and the Surprising Robustness of HMMs

Suppose that we are given a time series where consecutive samples are believed to come from a probabilistic source, that the source changes from time to time and that the total number of sources is fixed. Our objective is to estimate the distributions of the sources. A standard approach to this problem is to model the data as a hidden Markov model (HMM). However, since the data often lacks the Markov or the stationarity properties of an HMM, one can ask whether this approach is still suitable or perhaps another approach is required. In this paper we show that a maximum likelihood HMM estimator can be used to approximate the source distributions in a much larger class of models than HMMs. Specifically, we propose a natural and fairly general non-stationary model of the data, where the only restriction is that the sources do not change too often. Our main result shows that for this model, a maximum-likelihood HMM estimator produces the correct second moment of the data, and the results can be extended to higher moments.