Whats Missing? Learning Hidden Markov Models When the Locations of Missing Observations are Unknown
Paper and Code
Mar 12, 2022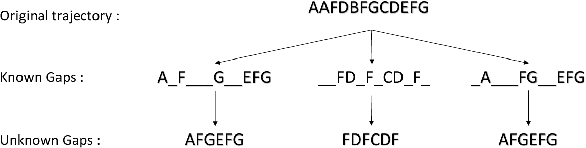
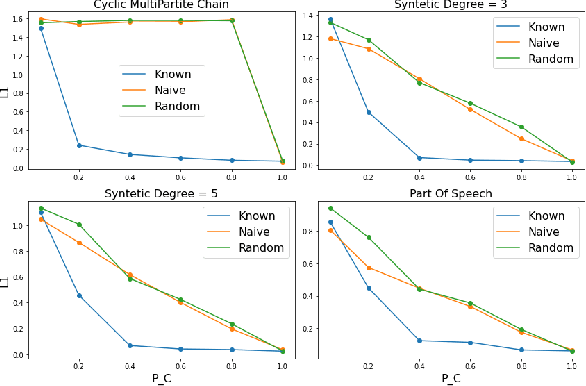
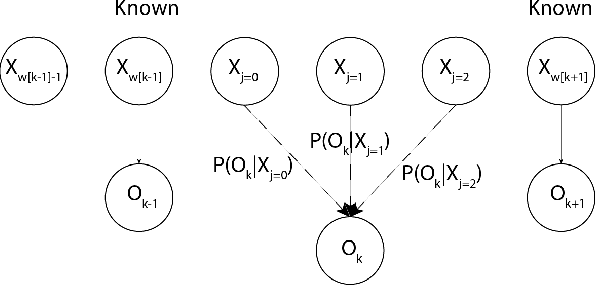
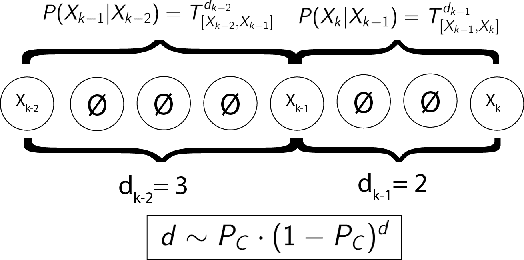
The Hidden Markov Model (HMM) is one of the most widely used statistical models for sequential data analysis, and it has been successfully applied in a large variety of domains. One of the key reasons for this versatility is the ability of HMMs to deal with missing data. However, standard HMM learning algorithms rely crucially on the assumption that the positions of the missing observations within the observation sequence are known. In some situations where such assumptions are not feasible, a number of special algorithms have been developed. Currently, these algorithms rely strongly on specific structural assumptions of the underlying chain, such as acyclicity, and are not applicable in the general case. In particular, there are numerous domains within medicine and computational biology, where the missing observation locations are unknown and acyclicity assumptions do not hold, thus presenting a barrier for the application of HMMs in those fields. In this paper we consider a general problem of learning HMMs from data with unknown missing observation locations (i.e., only the order of the non-missing observations are known). We introduce a generative model of the location omissions and propose two learning methods for this model, a (semi) analytic approach, and a Gibbs sampler. We evaluate and compare the algorithms in a variety of scenarios, measuring their reconstruction precision and robustness under model misspecification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge