Efficient Fairness-Performance Pareto Front Computation

There is a well known intrinsic trade-off between the fairness of a representation and the performance of classifiers derived from the representation. Due to the complexity of optimisation algorithms in most modern representation learning approaches, for a given method it may be non-trivial to decide whether the obtained fairness-performance curve of the method is optimal, i.e., whether it is close to the true Pareto front for these quantities for the underlying data distribution. In this paper we propose a new method to compute the optimal Pareto front, which does not require the training of complex representation models. We show that optimal fair representations possess several useful structural properties, and that these properties enable a reduction of the computation of the Pareto Front to a compact discrete problem. We then also show that these compact approximating problems can be efficiently solved via off-the shelf concave-convex programming methods. Since our approach is independent of the specific model of representations, it may be used as the benchmark to which representation learning algorithms may be compared. We experimentally evaluate the approach on a number of real world benchmark datasets.

Implicitly Normalized Explicitly Regularized Density Estimation

We propose a new approach to non-parametric density estimation, that is based on regularizing a Sobolev norm of the density. This method is provably different from Kernel Density Estimation, and makes the bias of the model clear and interpretable. While there is no closed analytic form for the associated kernel, we show that one can approximate it using sampling. The optimization problem needed to determine the density is non-convex, and standard gradient methods do not perform well. However, we show that with an appropriate initialization and using natural gradients, one can obtain well performing solutions. Finally, while the approach provides unnormalized densities, which prevents the use of log-likelihood for cross validation, we show that one can instead adapt Fisher Divergence based Score Matching methods for this task. We evaluate the resulting method on the comprehensive recent Anomaly Detection benchmark suite, ADBench, and find that it ranks second best, among more than 15 algorithms.

Whats Missing? Learning Hidden Markov Models When the Locations of Missing Observations are Unknown

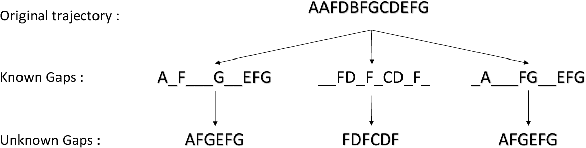
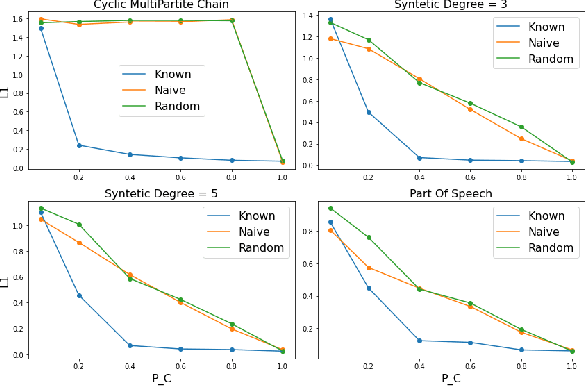
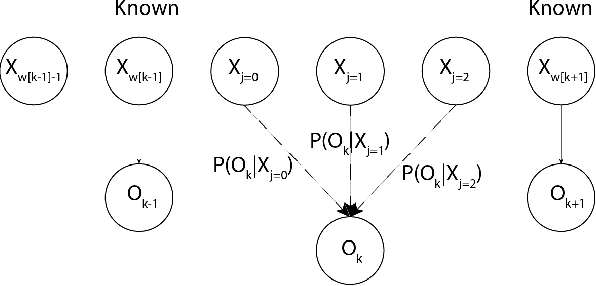
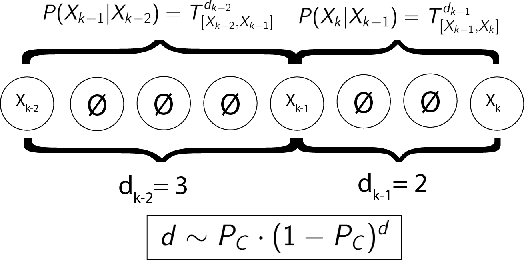
The Hidden Markov Model (HMM) is one of the most widely used statistical models for sequential data analysis, and it has been successfully applied in a large variety of domains. One of the key reasons for this versatility is the ability of HMMs to deal with missing data. However, standard HMM learning algorithms rely crucially on the assumption that the positions of the missing observations within the observation sequence are known. In some situations where such assumptions are not feasible, a number of special algorithms have been developed. Currently, these algorithms rely strongly on specific structural assumptions of the underlying chain, such as acyclicity, and are not applicable in the general case. In particular, there are numerous domains within medicine and computational biology, where the missing observation locations are unknown and acyclicity assumptions do not hold, thus presenting a barrier for the application of HMMs in those fields. In this paper we consider a general problem of learning HMMs from data with unknown missing observation locations (i.e., only the order of the non-missing observations are known). We introduce a generative model of the location omissions and propose two learning methods for this model, a (semi) analytic approach, and a Gibbs sampler. We evaluate and compare the algorithms in a variety of scenarios, measuring their reconstruction precision and robustness under model misspecification.