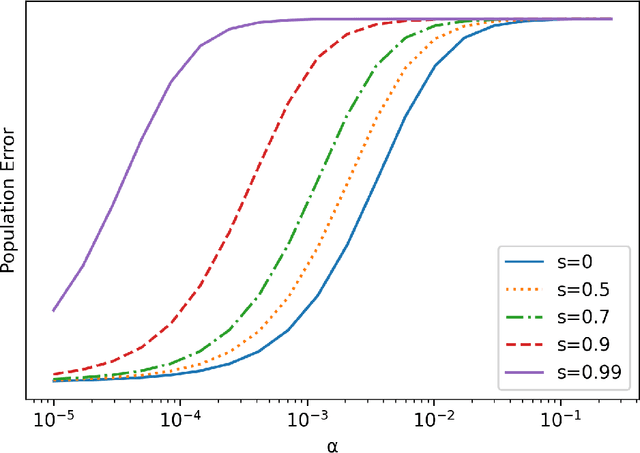
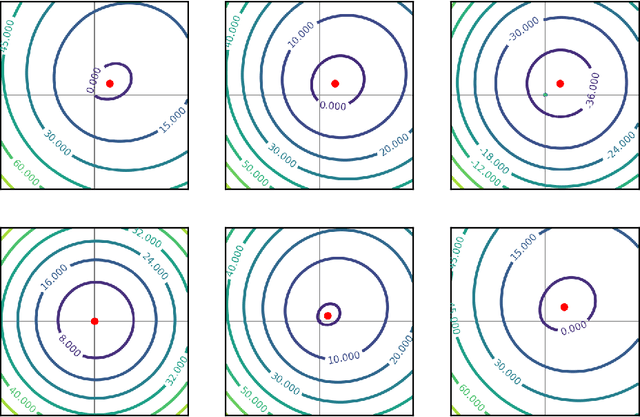
On the Implicit Bias of Initialization Shape: Beyond Infinitesimal Mirror Descent

Recent work has highlighted the role of initialization scale in determining the structure of the solutions that gradient methods converge to. In particular, it was shown that large initialization leads to the neural tangent kernel regime solution, whereas small initialization leads to so called "rich regimes". However, the initialization structure is richer than the overall scale alone and involves relative magnitudes of different weights and layers in the network. Here we show that these relative scales, which we refer to as initialization shape, play an important role in determining the learned model. We develop a novel technique for deriving the inductive bias of gradient-flow and use it to obtain closed-form implicit regularizers for multiple cases of interest.

Holdout SGD: Byzantine Tolerant Federated Learning

This work presents a new distributed Byzantine tolerant federated learning algorithm, HoldOut SGD, for Stochastic Gradient Descent (SGD) optimization. HoldOut SGD uses the well known machine learning technique of holdout estimation, in a distributed fashion, in order to select parameter updates that are likely to lead to models with low loss values. This makes it more effective at discarding Byzantine workers inputs than existing methods that eliminate outliers in the parameter-space of the learned model. HoldOut SGD first randomly selects a set of workers that use their private data in order to propose gradient updates. Next, a voting committee of workers is randomly selected, and each voter uses its private data as holdout data, in order to select the best proposals via a voting scheme. We propose two possible mechanisms for the coordination of workers in the distributed computation of HoldOut SGD. The first uses a truthful central server and corresponds to the typical setting of current federated learning. The second is fully distributed and requires no central server, paving the way to fully decentralized federated learning. The fully distributed version implements HoldOut SGD via ideas from the blockchain domain, and specifically the Algorand committee selection and consensus processes. We provide formal guarantees for the HoldOut SGD process in terms of its convergence to the optimal model, and its level of resilience to the fraction of Byzantine workers. Empirical evaluation shows that HoldOut SGD is Byzantine-resilient and efficiently converges to an effectual model for deep-learning tasks, as long as the total number of participating workers is large and the fraction of Byzantine workers is less than half (<1/3 for the fully distributed variant).