Task Agnostic Continual Learning Using Online Variational Bayes with Fixed-Point Updates

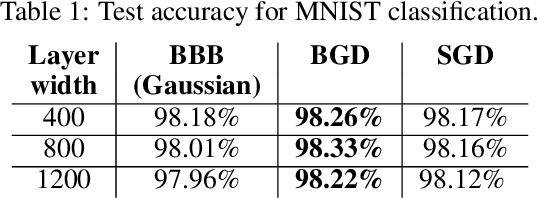
Background: Catastrophic forgetting is the notorious vulnerability of neural networks to the changes in the data distribution during learning. This phenomenon has long been considered a major obstacle for using learning agents in realistic continual learning settings. A large body of continual learning research assumes that task boundaries are known during training. However, only a few works consider scenarios in which task boundaries are unknown or not well defined -- task agnostic scenarios. The optimal Bayesian solution for this requires an intractable online Bayes update to the weights posterior. Contributions: We aim to approximate the online Bayes update as accurately as possible. To do so, we derive novel fixed-point equations for the online variational Bayes optimization problem, for multivariate Gaussian parametric distributions. By iterating the posterior through these fixed-point equations, we obtain an algorithm (FOO-VB) for continual learning which can handle non-stationary data distribution using a fixed architecture and without using external memory (i.e. without access to previous data). We demonstrate that our method (FOO-VB) outperforms existing methods in task agnostic scenarios. FOO-VB Pytorch implementation will be available online.

Kernel and Rich Regimes in Overparametrized Models

A recent line of work studies overparametrized neural networks in the "kernel regime," i.e. when the network behaves during training as a kernelized linear predictor, and thus training with gradient descent has the effect of finding the minimum RKHS norm solution. This stands in contrast to other studies which demonstrate how gradient descent on overparametrized multilayer networks can induce rich implicit biases that are not RKHS norms. Building on an observation by Chizat and Bach, we show how the scale of the initialization controls the transition between the "kernel" (aka lazy) and "rich" (aka active) regimes and affects generalization properties in multilayer homogeneous models. We also highlight an interesting role for the width of a model in the case that the predictor is not identically zero at initialization. We provide a complete and detailed analysis for a family of simple depth-$D$ models that already exhibit an interesting and meaningful transition between the kernel and rich regimes, and we also demonstrate this transition empirically for more complex matrix factorization models and multilayer non-linear networks.

Bayesian Gradient Descent: Online Variational Bayes Learning with Increased Robustness to Catastrophic Forgetting and Weight Pruning

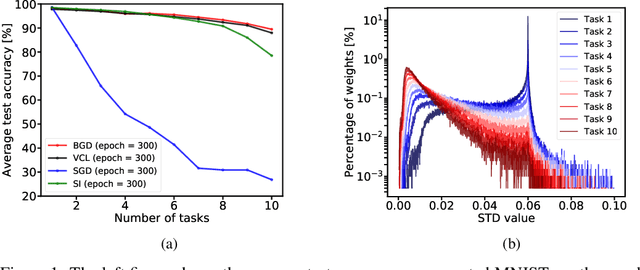
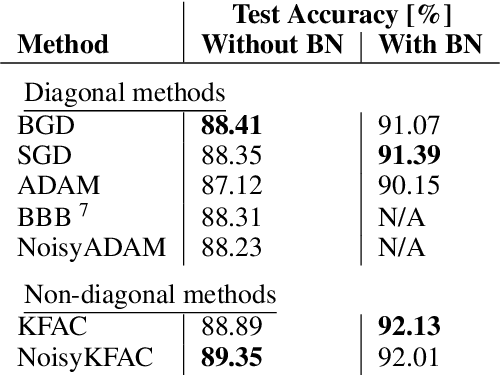
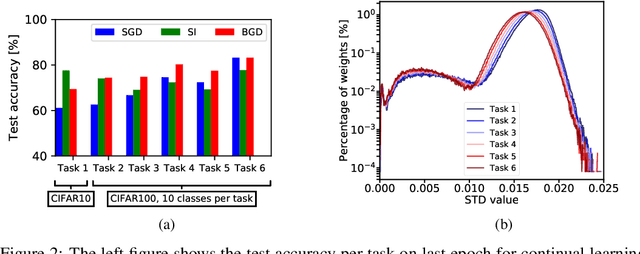
We suggest a novel approach for the estimation of the posterior distribution of the weights of a neural network, using an online version of the variational Bayes method. Having a confidence measure of the weights allows to combat several shortcomings of neural networks, such as their parameter redundancy, and their notorious vulnerability to the change of input distribution ("catastrophic forgetting"). Specifically, We show that this approach helps alleviate the catastrophic forgetting phenomenon - even without the knowledge of when the tasks are been switched. Furthermore, it improves the robustness of the network to weight pruning - even without re-training.

Norm matters: efficient and accurate normalization schemes in deep networks

Over the past few years batch-normalization has been commonly used in deep networks, allowing faster training and high performance for a wide variety of applications. However, the reasons behind its merits remained unanswered, with several shortcomings that hindered its use for certain tasks. In this work we present a novel view on the purpose and function of normalization methods and weight-decay, as tools to decouple weights' norm from the underlying optimized objective. We also improve the use of weight-normalization and show the connection between practices such as normalization, weight decay and learning-rate adjustments. Finally, we suggest several alternatives to the widely used $L^2$ batch-norm, using normalization in $L^1$ and $L^\infty$ spaces that can substantially improve numerical stability in low-precision implementations as well as provide computational and memory benefits. We demonstrate that such methods enable the first batch-norm alternative to work for half-precision implementations.