How do Minimum-Norm Shallow Denoisers Look in Function Space?

Neural network (NN) denoisers are an essential building block in many common tasks, ranging from image reconstruction to image generation. However, the success of these models is not well understood from a theoretical perspective. In this paper, we aim to characterize the functions realized by shallow ReLU NN denoisers -- in the common theoretical setting of interpolation (i.e., zero training loss) with a minimal representation cost (i.e., minimal $\ell^2$ norm weights). First, for univariate data, we derive a closed form for the NN denoiser function, find it is contractive toward the clean data points, and prove it generalizes better than the empirical MMSE estimator at a low noise level. Next, for multivariate data, we find the NN denoiser functions in a closed form under various geometric assumptions on the training data: data contained in a low-dimensional subspace, data contained in a union of one-sided rays, or several types of simplexes. These functions decompose into a sum of simple rank-one piecewise linear interpolations aligned with edges and/or faces connecting training samples. We empirically verify this alignment phenomenon on synthetic data and real images.

Task Agnostic Continual Learning Using Online Variational Bayes with Fixed-Point Updates

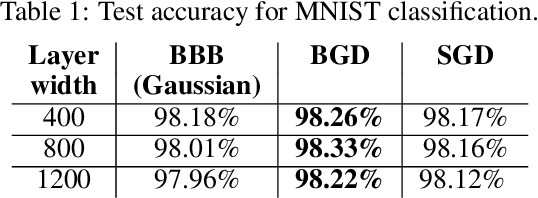
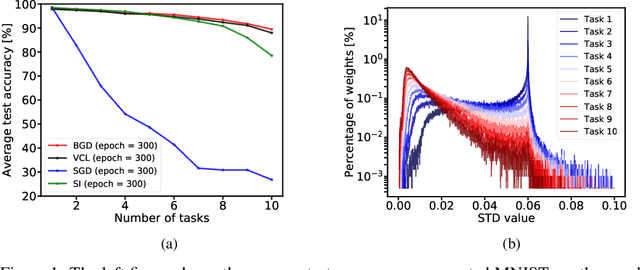
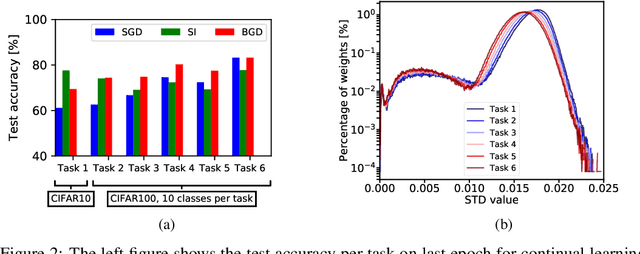
Background: Catastrophic forgetting is the notorious vulnerability of neural networks to the changes in the data distribution during learning. This phenomenon has long been considered a major obstacle for using learning agents in realistic continual learning settings. A large body of continual learning research assumes that task boundaries are known during training. However, only a few works consider scenarios in which task boundaries are unknown or not well defined -- task agnostic scenarios. The optimal Bayesian solution for this requires an intractable online Bayes update to the weights posterior. Contributions: We aim to approximate the online Bayes update as accurately as possible. To do so, we derive novel fixed-point equations for the online variational Bayes optimization problem, for multivariate Gaussian parametric distributions. By iterating the posterior through these fixed-point equations, we obtain an algorithm (FOO-VB) for continual learning which can handle non-stationary data distribution using a fixed architecture and without using external memory (i.e. without access to previous data). We demonstrate that our method (FOO-VB) outperforms existing methods in task agnostic scenarios. FOO-VB Pytorch implementation will be available online.

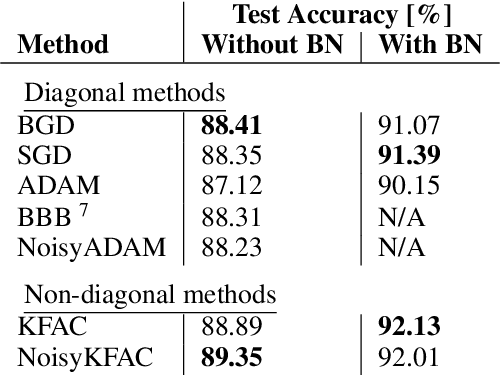
Bayesian Gradient Descent: Online Variational Bayes Learning with Increased Robustness to Catastrophic Forgetting and Weight Pruning

We suggest a novel approach for the estimation of the posterior distribution of the weights of a neural network, using an online version of the variational Bayes method. Having a confidence measure of the weights allows to combat several shortcomings of neural networks, such as their parameter redundancy, and their notorious vulnerability to the change of input distribution ("catastrophic forgetting"). Specifically, We show that this approach helps alleviate the catastrophic forgetting phenomenon - even without the knowledge of when the tasks are been switched. Furthermore, it improves the robustness of the network to weight pruning - even without re-training.