When Diffusion Models Memorize: Inductive Biases in Probability Flow of Minimum-Norm Shallow Neural Nets

While diffusion models generate high-quality images via probability flow, the theoretical understanding of this process remains incomplete. A key question is when probability flow converges to training samples or more general points on the data manifold. We analyze this by studying the probability flow of shallow ReLU neural network denoisers trained with minimal $\ell^2$ norm. For intuition, we introduce a simpler score flow and show that for orthogonal datasets, both flows follow similar trajectories, converging to a training point or a sum of training points. However, early stopping by the diffusion time scheduler allows probability flow to reach more general manifold points. This reflects the tendency of diffusion models to both memorize training samples and generate novel points that combine aspects of multiple samples, motivating our study of such behavior in simplified settings. We extend these results to obtuse simplex data and, through simulations in the orthogonal case, confirm that probability flow converges to a training point, a sum of training points, or a manifold point. Moreover, memorization decreases when the number of training samples grows, as fewer samples accumulate near training points.

DeepDIVE: Optimizing Input-Constrained Distributions for Composite DNA Storage via Multinomial Channel

We address the challenge of optimizing the capacity-achieving input distribution for a multinomial channel under the constraint of limited input support size, which is a crucial aspect in the design of DNA storage systems. We propose an algorithm that further elaborates the Multidimensional Dynamic Assignment Blahut-Arimoto (M-DAB) algorithm. Our proposed algorithm integrates variational autoencoder for determining the optimal locations of input distribution, into the alternating optimization of the input distribution locations and weights.

On Bits and Bandits: Quantifying the Regret-Information Trade-off

In interactive decision-making tasks, information can be acquired by direct interactions, through receiving indirect feedback, and from external knowledgeable sources. We examine the trade-off between the information an agent accumulates and the regret it suffers. We show that information from external sources, measured in bits, can be traded off for regret, measured in reward. We invoke information-theoretic methods for obtaining regret lower bounds, that also allow us to easily re-derive several known lower bounds. We then generalize a variety of interactive decision-making tasks with external information to a new setting. Using this setting, we introduce the first Bayesian regret lower bounds that depend on the information an agent accumulates. These lower bounds also prove the near-optimality of Thompson sampling for Bayesian problems. Finally, we demonstrate the utility of these bounds in improving the performance of a question-answering task with large language models, allowing us to obtain valuable insights.

A representation-learning game for classes of prediction tasks

We propose a game-based formulation for learning dimensionality-reducing representations of feature vectors, when only a prior knowledge on future prediction tasks is available. In this game, the first player chooses a representation, and then the second player adversarially chooses a prediction task from a given class, representing the prior knowledge. The first player aims is to minimize, and the second player to maximize, the regret: The minimal prediction loss using the representation, compared to the same loss using the original features. For the canonical setting in which the representation, the response to predict and the predictors are all linear functions, and under the mean squared error loss function, we derive the theoretically optimal representation in pure strategies, which shows the effectiveness of the prior knowledge, and the optimal regret in mixed strategies, which shows the usefulness of randomizing the representation. For general representations and loss functions, we propose an efficient algorithm to optimize a randomized representation. The algorithm only requires the gradients of the loss function, and is based on incrementally adding a representation rule to a mixture of such rules.

Statistical curriculum learning: An elimination algorithm achieving an oracle risk

We consider a statistical version of curriculum learning (CL) in a parametric prediction setting. The learner is required to estimate a target parameter vector, and can adaptively collect samples from either the target model, or other source models that are similar to the target model, but less noisy. We consider three types of learners, depending on the level of side-information they receive. The first two, referred to as strong/weak-oracle learners, receive high/low degrees of information about the models, and use these to learn. The third, a fully adaptive learner, estimates the target parameter vector without any prior information. In the single source case, we propose an elimination learning method, whose risk matches that of a strong-oracle learner. In the multiple source case, we advocate that the risk of the weak-oracle learner is a realistic benchmark for the risk of adaptive learners. We develop an adaptive multiple elimination-rounds CL algorithm, and characterize instance-dependent conditions for its risk to match that of the weak-oracle learner. We consider instance-dependent minimax lower bounds, and discuss the challenges associated with defining the class of instances for the bound. We derive two minimax lower bounds, and determine the conditions under which the performance weak-oracle learner is minimax optimal.

Characterization of the Distortion-Perception Tradeoff for Finite Channels with Arbitrary Metrics

Whenever inspected by humans, reconstructed signals should not be distinguished from real ones. Typically, such a high perceptual quality comes at the price of high reconstruction error, and vice versa. We study this distortion-perception (DP) tradeoff over finite-alphabet channels, for the Wasserstein-$1$ distance induced by a general metric as the perception index, and an arbitrary distortion matrix. Under this setting, we show that computing the DP function and the optimal reconstructions is equivalent to solving a set of linear programming problems. We provide a structural characterization of the DP tradeoff, where the DP function is piecewise linear in the perception index. We further derive a closed-form expression for the case of binary sources.

The Joint Effect of Task Similarity and Overparameterization on Catastrophic Forgetting -- An Analytical Model

In continual learning, catastrophic forgetting is affected by multiple aspects of the tasks. Previous works have analyzed separately how forgetting is affected by either task similarity or overparameterization. In contrast, our paper examines how task similarity and overparameterization jointly affect forgetting in an analyzable model. Specifically, we focus on two-task continual linear regression, where the second task is a random orthogonal transformation of an arbitrary first task (an abstraction of random permutation tasks). We derive an exact analytical expression for the expected forgetting - and uncover a nuanced pattern. In highly overparameterized models, intermediate task similarity causes the most forgetting. However, near the interpolation threshold, forgetting decreases monotonically with the expected task similarity. We validate our findings with linear regression on synthetic data, and with neural networks on established permutation task benchmarks.

Maximal-Capacity Discrete Memoryless Channel Identification

The problem of identifying the channel with the highest capacity among several discrete memoryless channels (DMCs) is considered. The problem is cast as a pure-exploration multi-armed bandit problem, which follows the practical use of training sequences to sense the communication channel statistics. A capacity estimator is proposed and tight confidence bounds on the estimator error are derived. Based on this capacity estimator, a gap-elimination algorithm termed BestChanID is proposed, which is oblivious to the capacity-achieving input distribution and is guaranteed to output the DMC with the largest capacity, with a desired confidence. Furthermore, two additional algorithms NaiveChanSel and MedianChanEl, that output with certain confidence a DMC with capacity close to the maximal, are introduced. Each of those algorithms is beneficial in a different regime and can be used as a subroutine in BestChanID. The sample complexity of all algorithms is analyzed as a function of the desired confidence parameter, the number of channels, and the channels' input and output alphabet sizes. The cost of best channel identification is shown to scale quadratically with the alphabet size, and a fundamental lower bound for the required number of channel senses to identify the best channel with a certain confidence is derived.

How do Minimum-Norm Shallow Denoisers Look in Function Space?

Neural network (NN) denoisers are an essential building block in many common tasks, ranging from image reconstruction to image generation. However, the success of these models is not well understood from a theoretical perspective. In this paper, we aim to characterize the functions realized by shallow ReLU NN denoisers -- in the common theoretical setting of interpolation (i.e., zero training loss) with a minimal representation cost (i.e., minimal $\ell^2$ norm weights). First, for univariate data, we derive a closed form for the NN denoiser function, find it is contractive toward the clean data points, and prove it generalizes better than the empirical MMSE estimator at a low noise level. Next, for multivariate data, we find the NN denoiser functions in a closed form under various geometric assumptions on the training data: data contained in a low-dimensional subspace, data contained in a union of one-sided rays, or several types of simplexes. These functions decompose into a sum of simple rank-one piecewise linear interpolations aligned with edges and/or faces connecting training samples. We empirically verify this alignment phenomenon on synthetic data and real images.

Multi-Armed Bandits with Self-Information Rewards

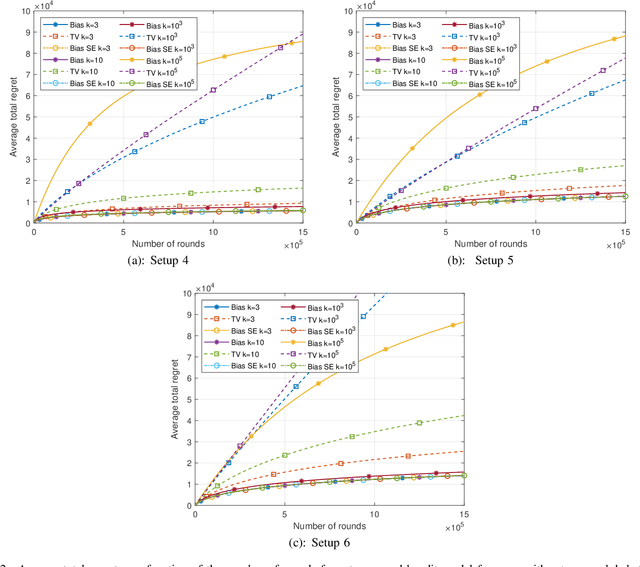
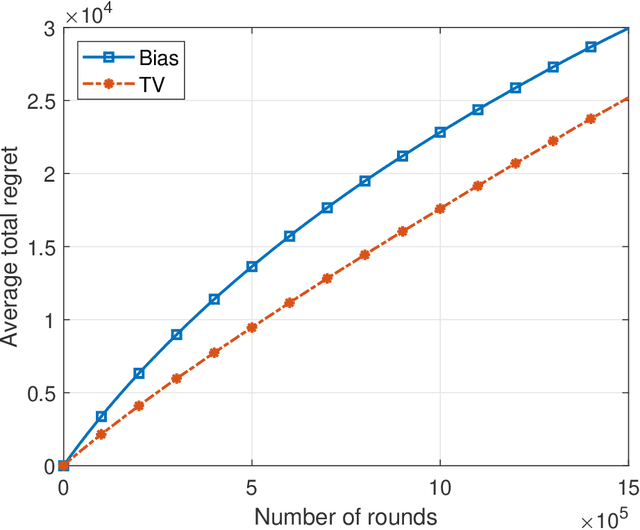
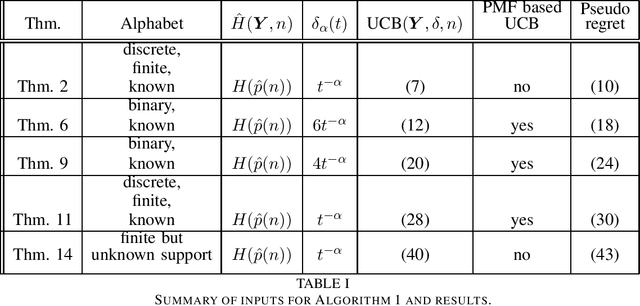
This paper introduces the informational multi-armed bandit (IMAB) model in which at each round, a player chooses an arm, observes a symbol, and receives an unobserved reward in the form of the symbol's self-information. Thus, the expected reward of an arm is the Shannon entropy of the probability mass function of the source that generates its symbols. The player aims to maximize the expected total reward associated with the entropy values of the arms played. Under the assumption that the alphabet size is known, two UCB-based algorithms are proposed for the IMAB model which consider the biases of the plug-in entropy estimator. The first algorithm optimistically corrects the bias term in the entropy estimation. The second algorithm relies on data-dependent confidence intervals that adapt to sources with small entropy values. Performance guarantees are provided by upper bounding the expected regret of each of the algorithms. Furthermore, in the Bernoulli case, the asymptotic behavior of these algorithms is compared to the Lai-Robbins lower bound for the pseudo regret. Additionally, under the assumption that the \textit{exact} alphabet size is unknown, and instead the player only knows a loose upper bound on it, a UCB-based algorithm is proposed, in which the player aims to reduce the regret caused by the unknown alphabet size in a finite time regime. Numerical results illustrating the expected regret of the algorithms presented in the paper are provided.