Multi-Armed Bandits with Self-Information Rewards
Paper and Code
Sep 06, 2022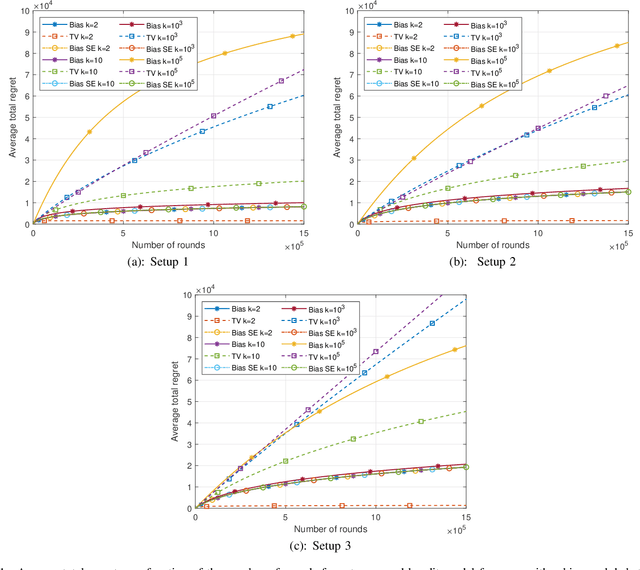
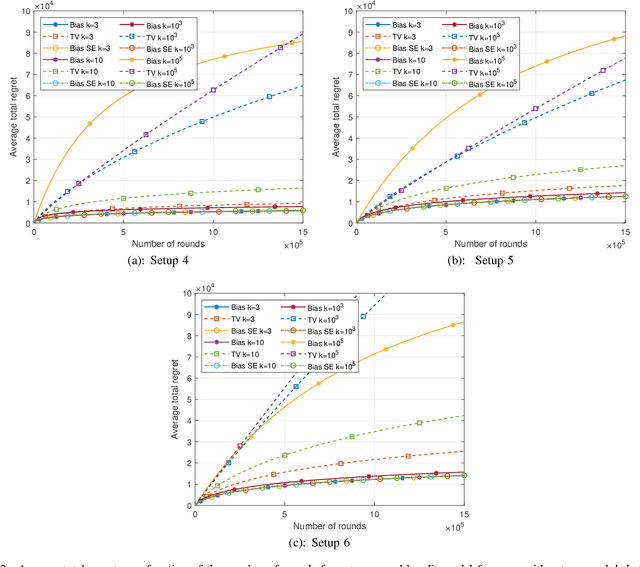
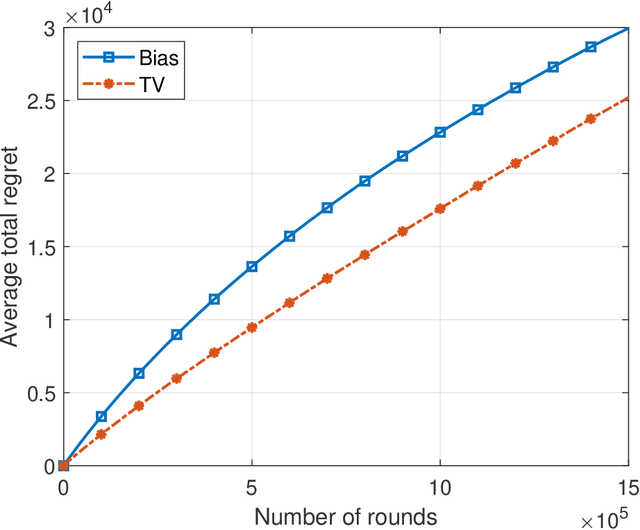
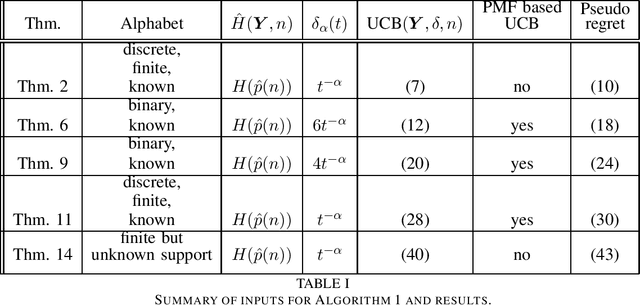
This paper introduces the informational multi-armed bandit (IMAB) model in which at each round, a player chooses an arm, observes a symbol, and receives an unobserved reward in the form of the symbol's self-information. Thus, the expected reward of an arm is the Shannon entropy of the probability mass function of the source that generates its symbols. The player aims to maximize the expected total reward associated with the entropy values of the arms played. Under the assumption that the alphabet size is known, two UCB-based algorithms are proposed for the IMAB model which consider the biases of the plug-in entropy estimator. The first algorithm optimistically corrects the bias term in the entropy estimation. The second algorithm relies on data-dependent confidence intervals that adapt to sources with small entropy values. Performance guarantees are provided by upper bounding the expected regret of each of the algorithms. Furthermore, in the Bernoulli case, the asymptotic behavior of these algorithms is compared to the Lai-Robbins lower bound for the pseudo regret. Additionally, under the assumption that the \textit{exact} alphabet size is unknown, and instead the player only knows a loose upper bound on it, a UCB-based algorithm is proposed, in which the player aims to reduce the regret caused by the unknown alphabet size in a finite time regime. Numerical results illustrating the expected regret of the algorithms presented in the paper are provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge