On Bits and Bandits: Quantifying the Regret-Information Trade-off

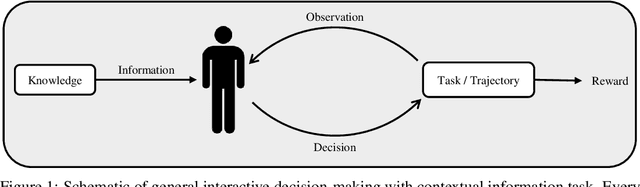
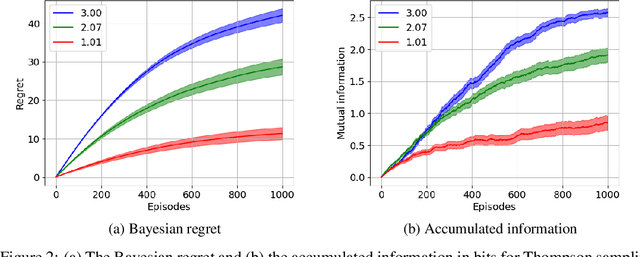
In interactive decision-making tasks, information can be acquired by direct interactions, through receiving indirect feedback, and from external knowledgeable sources. We examine the trade-off between the information an agent accumulates and the regret it suffers. We show that information from external sources, measured in bits, can be traded off for regret, measured in reward. We invoke information-theoretic methods for obtaining regret lower bounds, that also allow us to easily re-derive several known lower bounds. We then generalize a variety of interactive decision-making tasks with external information to a new setting. Using this setting, we introduce the first Bayesian regret lower bounds that depend on the information an agent accumulates. These lower bounds also prove the near-optimality of Thompson sampling for Bayesian problems. Finally, we demonstrate the utility of these bounds in improving the performance of a question-answering task with large language models, allowing us to obtain valuable insights.

On the Global Convergence of Policy Gradient in Average Reward Markov Decision Processes

We present the first finite time global convergence analysis of policy gradient in the context of infinite horizon average reward Markov decision processes (MDPs). Specifically, we focus on ergodic tabular MDPs with finite state and action spaces. Our analysis shows that the policy gradient iterates converge to the optimal policy at a sublinear rate of $O\left({\frac{1}{T}}\right),$ which translates to $O\left({\log(T)}\right)$ regret, where $T$ represents the number of iterations. Prior work on performance bounds for discounted reward MDPs cannot be extended to average reward MDPs because the bounds grow proportional to the fifth power of the effective horizon. Thus, our primary contribution is in proving that the policy gradient algorithm converges for average-reward MDPs and in obtaining finite-time performance guarantees. In contrast to the existing discounted reward performance bounds, our performance bounds have an explicit dependence on constants that capture the complexity of the underlying MDP. Motivated by this observation, we reexamine and improve the existing performance bounds for discounted reward MDPs. We also present simulations to empirically evaluate the performance of average reward policy gradient algorithm.