Towards Cheaper Inference in Deep Networks with Lower Bit-Width Accumulators

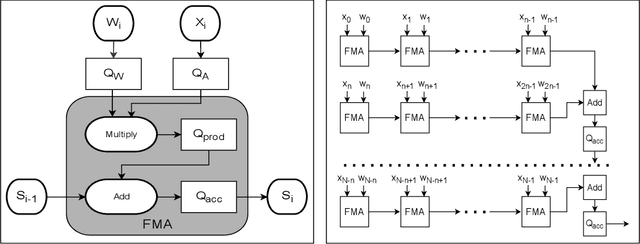
The majority of the research on the quantization of Deep Neural Networks (DNNs) is focused on reducing the precision of tensors visible by high-level frameworks (e.g., weights, activations, and gradients). However, current hardware still relies on high-accuracy core operations. Most significant is the operation of accumulating products. This high-precision accumulation operation is gradually becoming the main computational bottleneck. This is because, so far, the usage of low-precision accumulators led to a significant degradation in performance. In this work, we present a simple method to train and fine-tune high-end DNNs, to allow, for the first time, utilization of cheaper, $12$-bits accumulators, with no significant degradation in accuracy. Lastly, we show that as we decrease the accumulation precision further, using fine-grained gradient approximations can improve the DNN accuracy.

How do Minimum-Norm Shallow Denoisers Look in Function Space?

Neural network (NN) denoisers are an essential building block in many common tasks, ranging from image reconstruction to image generation. However, the success of these models is not well understood from a theoretical perspective. In this paper, we aim to characterize the functions realized by shallow ReLU NN denoisers -- in the common theoretical setting of interpolation (i.e., zero training loss) with a minimal representation cost (i.e., minimal $\ell^2$ norm weights). First, for univariate data, we derive a closed form for the NN denoiser function, find it is contractive toward the clean data points, and prove it generalizes better than the empirical MMSE estimator at a low noise level. Next, for multivariate data, we find the NN denoiser functions in a closed form under various geometric assumptions on the training data: data contained in a low-dimensional subspace, data contained in a union of one-sided rays, or several types of simplexes. These functions decompose into a sum of simple rank-one piecewise linear interpolations aligned with edges and/or faces connecting training samples. We empirically verify this alignment phenomenon on synthetic data and real images.

Beyond Signal Propagation: Is Feature Diversity Necessary in Deep Neural Network Initialization?

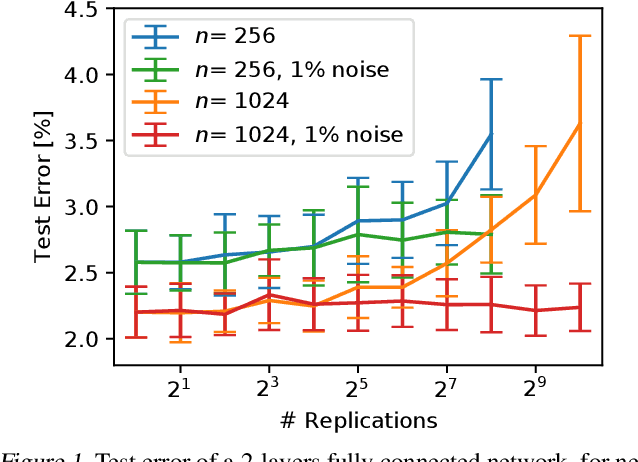
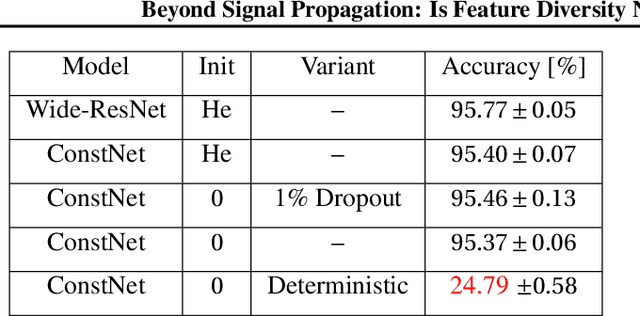
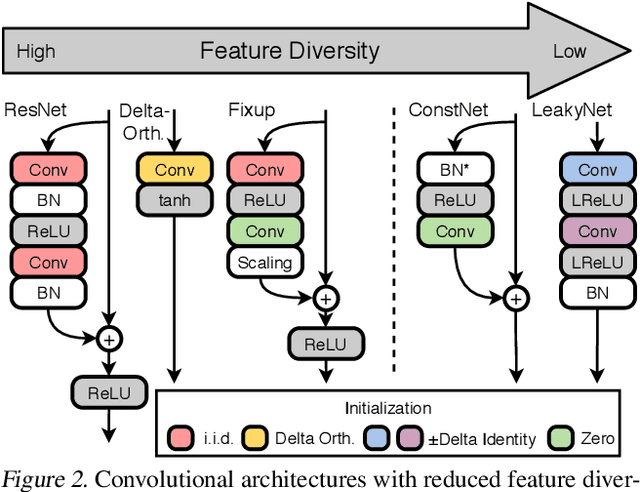
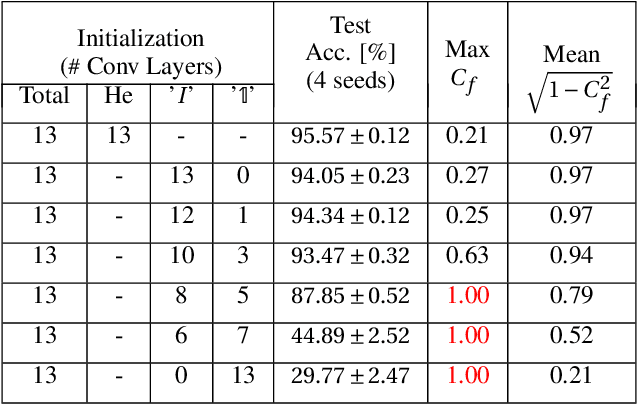
Deep neural networks are typically initialized with random weights, with variances chosen to facilitate signal propagation and stable gradients. It is also believed that diversity of features is an important property of these initializations. We construct a deep convolutional network with identical features by initializing almost all the weights to $0$. The architecture also enables perfect signal propagation and stable gradients, and achieves high accuracy on standard benchmarks. This indicates that random, diverse initializations are \textit{not} necessary for training neural networks. An essential element in training this network is a mechanism of symmetry breaking; we study this phenomenon and find that standard GPU operations, which are non-deterministic, can serve as a sufficient source of symmetry breaking to enable training.

Is Feature Diversity Necessary in Neural Network Initialization?

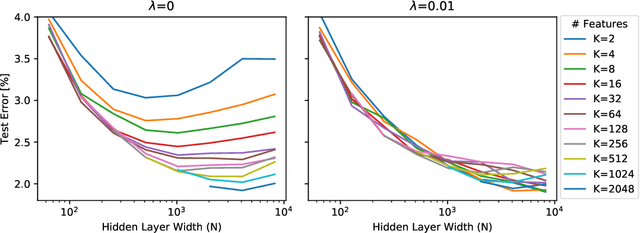
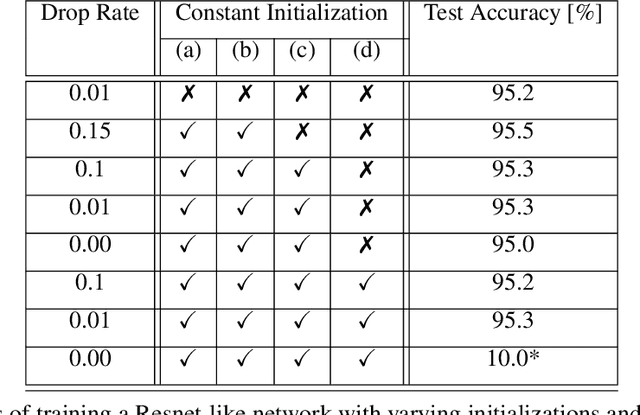
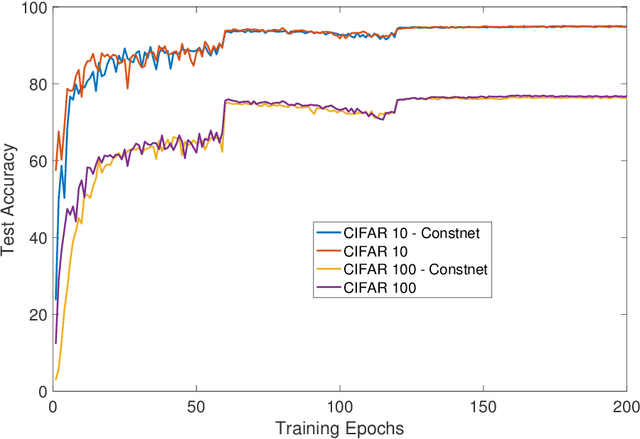
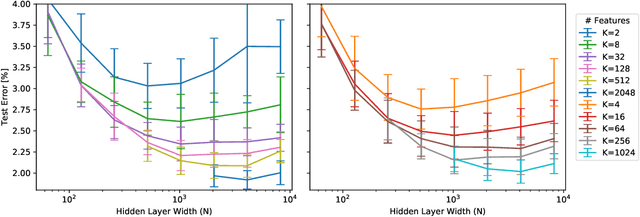
Standard practice in training neural networks involves initializing the weights in an independent fashion. The results of recent work suggest that feature "diversity" at initialization plays an important role in training the network. However, other initialization schemes with reduced feature diversity have also been shown to be viable. In this work, we conduct a series of experiments aimed at elucidating the importance of feature diversity at initialization. We show that a complete lack of diversity is harmful to training, but its effects can be counteracted by a relatively small addition of noise - even the noise in standard non-deterministic GPU computations is sufficient. Furthermore, we construct a deep convolutional network with identical features at initialization and almost all of the weights initialized at 0 that can be trained to reach accuracy matching its standard-initialized counterpart.

A Mean Field Theory of Quantized Deep Networks: The Quantization-Depth Trade-Off

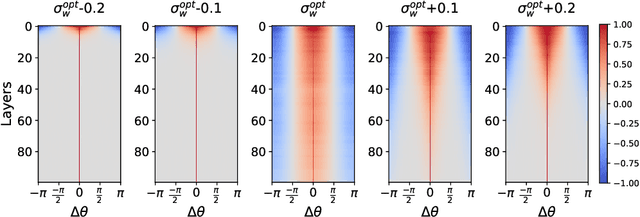
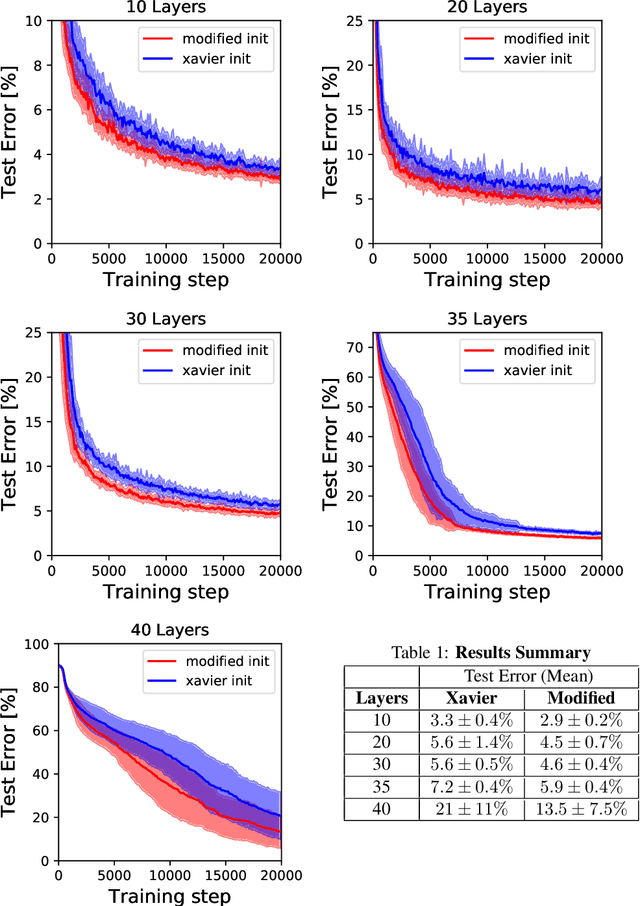
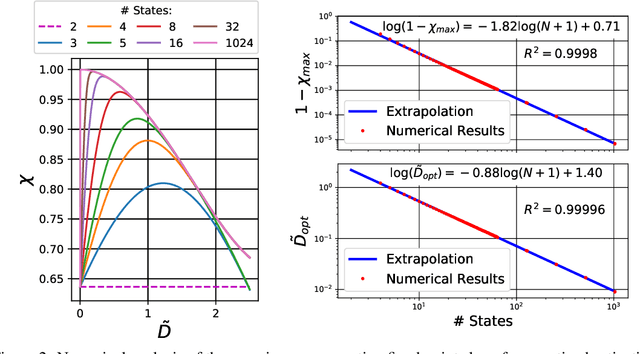
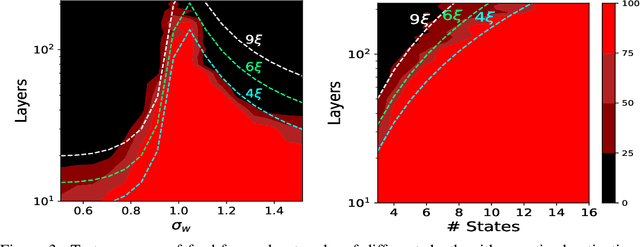
Reducing the precision of weights and activation functions in neural network training, with minimal impact on performance, is essential for the deployment of these models in resource-constrained environments. We apply mean-field techniques to networks with quantized activations in order to evaluate the degree to which quantization degrades signal propagation at initialization. We derive initialization schemes which maximize signal propagation in such networks and suggest why this is helpful for generalization. Building on these results, we obtain a closed form implicit equation for $L_{\max}$, the maximal trainable depth (and hence model capacity), given $N$, the number of quantization levels in the activation function. Solving this equation numerically, we obtain asymptotically: $L_{\max}\propto N^{1.82}$.