Quantum advantage for learning shallow neural networks with natural data distributions

The application of quantum computers to machine learning tasks is an exciting potential direction to explore in search of quantum advantage. In the absence of large quantum computers to empirically evaluate performance, theoretical frameworks such as the quantum probably approximately correct (PAC) and quantum statistical query (QSQ) models have been proposed to study quantum algorithms for learning classical functions. Despite numerous works investigating quantum advantage in these models, we nevertheless only understand it at two extremes: either exponential quantum advantages for uniform input distributions or no advantage for potentially adversarial distributions. In this work, we study the gap between these two regimes by designing an efficient quantum algorithm for learning periodic neurons in the QSQ model over a broad range of non-uniform distributions, which includes Gaussian, generalized Gaussian, and logistic distributions. To our knowledge, our work is also the first result in quantum learning theory for classical functions that explicitly considers real-valued functions. Recent advances in classical learning theory prove that learning periodic neurons is hard for any classical gradient-based algorithm, giving us an exponential quantum advantage over such algorithms, which are the standard workhorses of machine learning. Moreover, in some parameter regimes, the problem remains hard for classical statistical query algorithms and even general classical algorithms learning under small amounts of noise.

Exponential Quantum Communication Advantage in Distributed Learning

Training and inference with large machine learning models that far exceed the memory capacity of individual devices necessitates the design of distributed architectures, forcing one to contend with communication constraints. We present a framework for distributed computation over a quantum network in which data is encoded into specialized quantum states. We prove that for certain models within this framework, inference and training using gradient descent can be performed with exponentially less communication compared to their classical analogs, and with relatively modest time and space complexity overheads relative to standard gradient-based methods. To our knowledge, this is the first example of exponential quantum advantage for a generic class of machine learning problems with dense classical data that holds regardless of the data encoding cost. Moreover, we show that models in this class can encode highly nonlinear features of their inputs, and their expressivity increases exponentially with model depth. We also find that, interestingly, the communication advantage nearly vanishes for simpler linear classifiers. These results can be combined with natural privacy advantages in the communicated quantum states that limit the amount of information that can be extracted from them about the data and model parameters. Taken as a whole, these findings form a promising foundation for distributed machine learning over quantum networks.

On quantum backpropagation, information reuse, and cheating measurement collapse

The success of modern deep learning hinges on the ability to train neural networks at scale. Through clever reuse of intermediate information, backpropagation facilitates training through gradient computation at a total cost roughly proportional to running the function, rather than incurring an additional factor proportional to the number of parameters - which can now be in the trillions. Naively, one expects that quantum measurement collapse entirely rules out the reuse of quantum information as in backpropagation. But recent developments in shadow tomography, which assumes access to multiple copies of a quantum state, have challenged that notion. Here, we investigate whether parameterized quantum models can train as efficiently as classical neural networks. We show that achieving backpropagation scaling is impossible without access to multiple copies of a state. With this added ability, we introduce an algorithm with foundations in shadow tomography that matches backpropagation scaling in quantum resources while reducing classical auxiliary computational costs to open problems in shadow tomography. These results highlight the nuance of reusing quantum information for practical purposes and clarify the unique difficulties in training large quantum models, which could alter the course of quantum machine learning.

Beyond the Imitation Game: Quantifying and extrapolating the capabilities of language models

Language models demonstrate both quantitative improvement and new qualitative capabilities with increasing scale. Despite their potentially transformative impact, these new capabilities are as yet poorly characterized. In order to inform future research, prepare for disruptive new model capabilities, and ameliorate socially harmful effects, it is vital that we understand the present and near-future capabilities and limitations of language models. To address this challenge, we introduce the Beyond the Imitation Game benchmark (BIG-bench). BIG-bench currently consists of 204 tasks, contributed by 442 authors across 132 institutions. Task topics are diverse, drawing problems from linguistics, childhood development, math, common-sense reasoning, biology, physics, social bias, software development, and beyond. BIG-bench focuses on tasks that are believed to be beyond the capabilities of current language models. We evaluate the behavior of OpenAI's GPT models, Google-internal dense transformer architectures, and Switch-style sparse transformers on BIG-bench, across model sizes spanning millions to hundreds of billions of parameters. In addition, a team of human expert raters performed all tasks in order to provide a strong baseline. Findings include: model performance and calibration both improve with scale, but are poor in absolute terms (and when compared with rater performance); performance is remarkably similar across model classes, though with benefits from sparsity; tasks that improve gradually and predictably commonly involve a large knowledge or memorization component, whereas tasks that exhibit "breakthrough" behavior at a critical scale often involve multiple steps or components, or brittle metrics; social bias typically increases with scale in settings with ambiguous context, but this can be improved with prompting.

Deep Networks Provably Classify Data on Curves

Data with low-dimensional nonlinear structure are ubiquitous in engineering and scientific problems. We study a model problem with such structure -- a binary classification task that uses a deep fully-connected neural network to classify data drawn from two disjoint smooth curves on the unit sphere. Aside from mild regularity conditions, we place no restrictions on the configuration of the curves. We prove that when (i) the network depth is large relative to certain geometric properties that set the difficulty of the problem and (ii) the network width and number of samples is polynomial in the depth, randomly-initialized gradient descent quickly learns to correctly classify all points on the two curves with high probability. To our knowledge, this is the first generalization guarantee for deep networks with nonlinear data that depends only on intrinsic data properties. Our analysis proceeds by a reduction to dynamics in the neural tangent kernel (NTK) regime, where the network depth plays the role of a fitting resource in solving the classification problem. In particular, via fine-grained control of the decay properties of the NTK, we demonstrate that when the network is sufficiently deep, the NTK can be locally approximated by a translationally invariant operator on the manifolds and stably inverted over smooth functions, which guarantees convergence and generalization.

Marginalizable Density Models

Probability density models based on deep networks have achieved remarkable success in modeling complex high-dimensional datasets. However, unlike kernel density estimators, modern neural models do not yield marginals or conditionals in closed form, as these quantities require the evaluation of seldom tractable integrals. In this work, we present the Marginalizable Density Model Approximator (MDMA), a novel deep network architecture which provides closed form expressions for the probabilities, marginals and conditionals of any subset of the variables. The MDMA learns deep scalar representations for each individual variable and combines them via learned hierarchical tensor decompositions into a tractable yet expressive CDF, from which marginals and conditional densities are easily obtained. We illustrate the advantage of exact marginalizability in several tasks that are out of reach of previous deep network-based density estimation models, such as estimating mutual information between arbitrary subsets of variables, inferring causality by testing for conditional independence, and inference with missing data without the need for data imputation, outperforming state-of-the-art models on these tasks. The model also allows for parallelized sampling with only a logarithmic dependence of the time complexity on the number of variables.

Deep Networks and the Multiple Manifold Problem

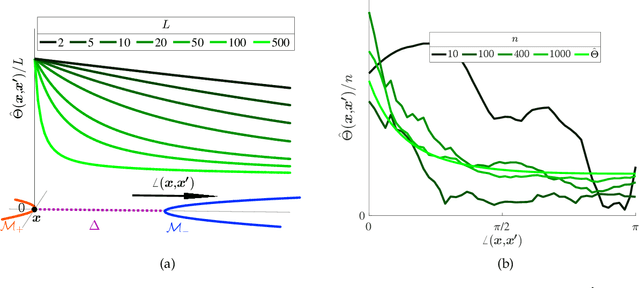
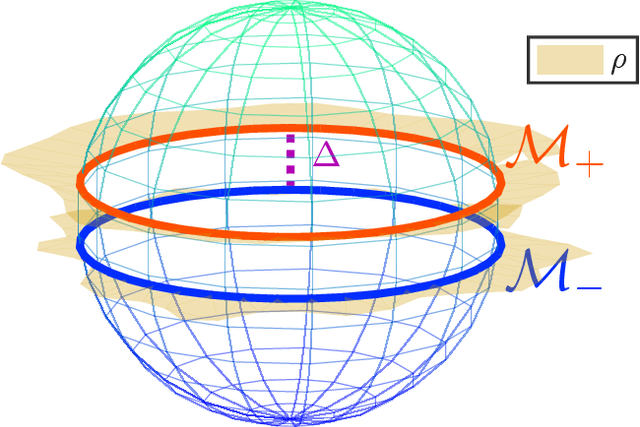
We study the multiple manifold problem, a binary classification task modeled on applications in machine vision, in which a deep fully-connected neural network is trained to separate two low-dimensional submanifolds of the unit sphere. We provide an analysis of the one-dimensional case, proving for a simple manifold configuration that when the network depth $L$ is large relative to certain geometric and statistical properties of the data, the network width $n$ grows as a sufficiently large polynomial in $L$, and the number of i.i.d. samples from the manifolds is polynomial in $L$, randomly-initialized gradient descent rapidly learns to classify the two manifolds perfectly with high probability. Our analysis demonstrates concrete benefits of depth and width in the context of a practically-motivated model problem: the depth acts as a fitting resource, with larger depths corresponding to smoother networks that can more readily separate the class manifolds, and the width acts as a statistical resource, enabling concentration of the randomly-initialized network and its gradients. The argument centers around the neural tangent kernel and its role in the nonasymptotic analysis of training overparameterized neural networks; to this literature, we contribute essentially optimal rates of concentration for the neural tangent kernel of deep fully-connected networks, requiring width $n \gtrsim L\,\mathrm{poly}(d_0)$ to achieve uniform concentration of the initial kernel over a $d_0$-dimensional submanifold of the unit sphere $\mathbb{S}^{n_0-1}$, and a nonasymptotic framework for establishing generalization of networks trained in the NTK regime with structured data. The proof makes heavy use of martingale concentration to optimally treat statistical dependencies across layers of the initial random network. This approach should be of use in establishing similar results for other network architectures.

Beyond Signal Propagation: Is Feature Diversity Necessary in Deep Neural Network Initialization?

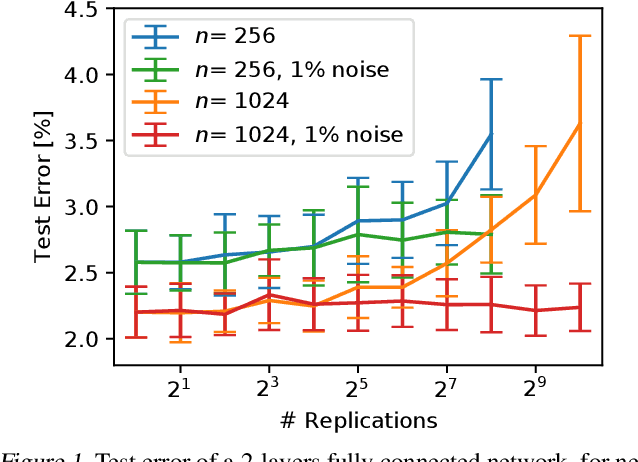
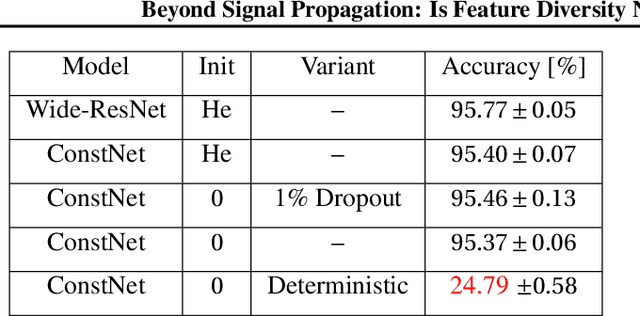
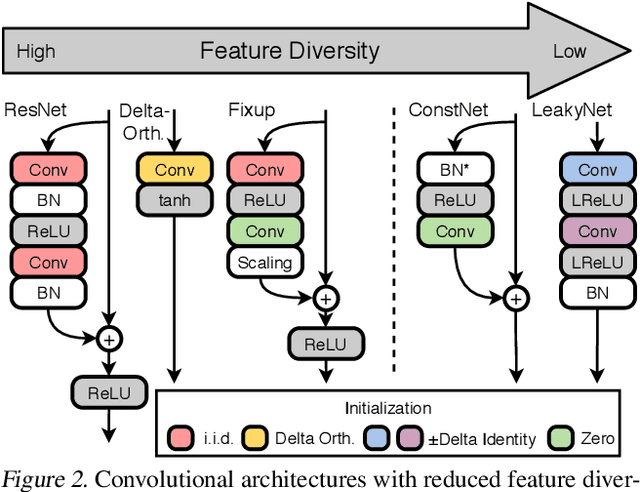
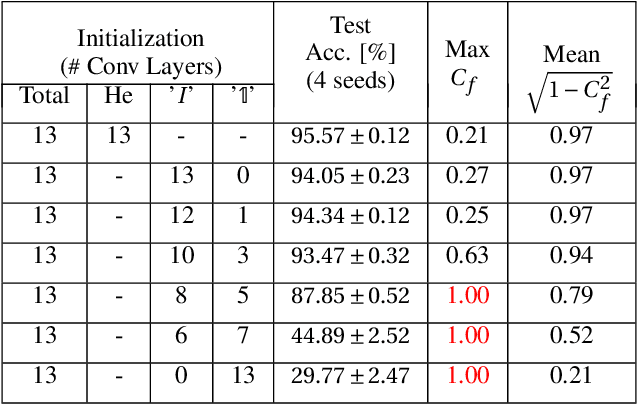
Deep neural networks are typically initialized with random weights, with variances chosen to facilitate signal propagation and stable gradients. It is also believed that diversity of features is an important property of these initializations. We construct a deep convolutional network with identical features by initializing almost all the weights to $0$. The architecture also enables perfect signal propagation and stable gradients, and achieves high accuracy on standard benchmarks. This indicates that random, diverse initializations are \textit{not} necessary for training neural networks. An essential element in training this network is a mechanism of symmetry breaking; we study this phenomenon and find that standard GPU operations, which are non-deterministic, can serve as a sufficient source of symmetry breaking to enable training.

Is Feature Diversity Necessary in Neural Network Initialization?

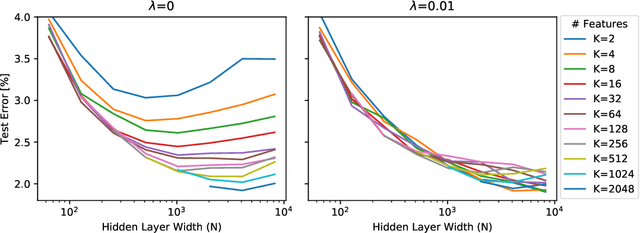
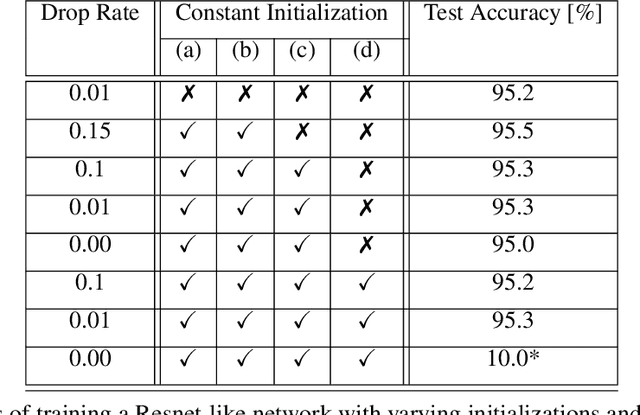
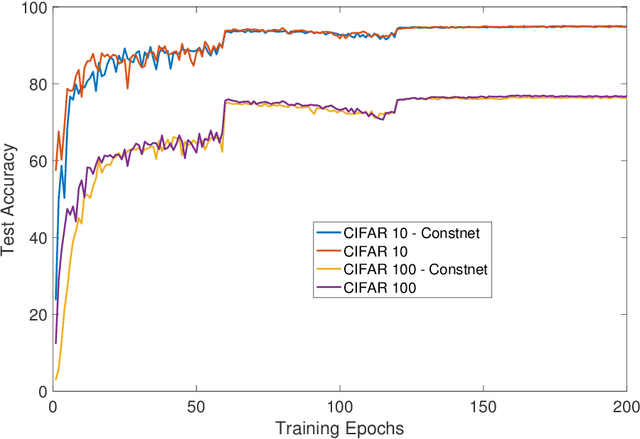
Standard practice in training neural networks involves initializing the weights in an independent fashion. The results of recent work suggest that feature "diversity" at initialization plays an important role in training the network. However, other initialization schemes with reduced feature diversity have also been shown to be viable. In this work, we conduct a series of experiments aimed at elucidating the importance of feature diversity at initialization. We show that a complete lack of diversity is harmful to training, but its effects can be counteracted by a relatively small addition of noise - even the noise in standard non-deterministic GPU computations is sufficient. Furthermore, we construct a deep convolutional network with identical features at initialization and almost all of the weights initialized at 0 that can be trained to reach accuracy matching its standard-initialized counterpart.

Wider Networks Learn Better Features

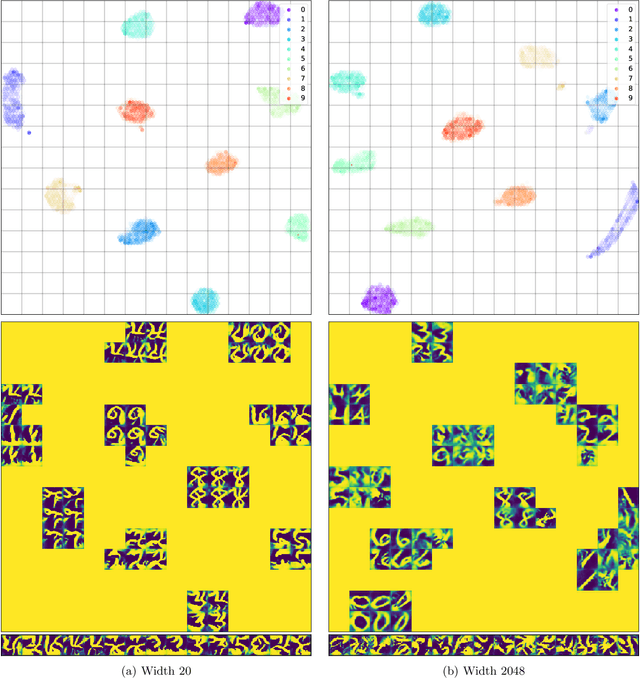
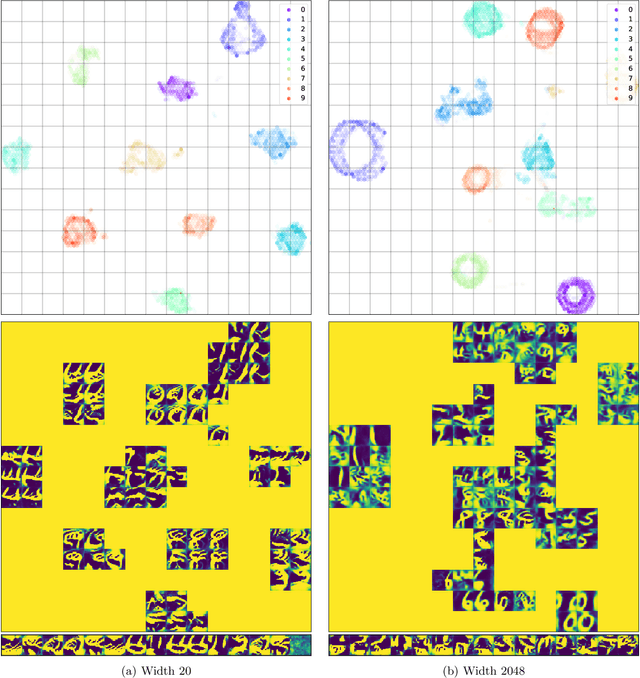
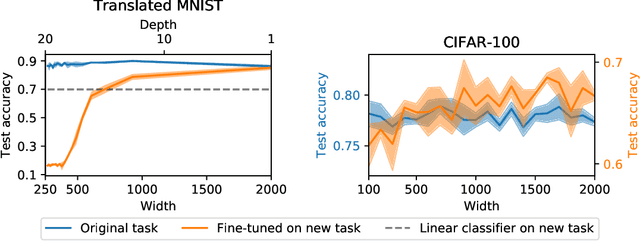
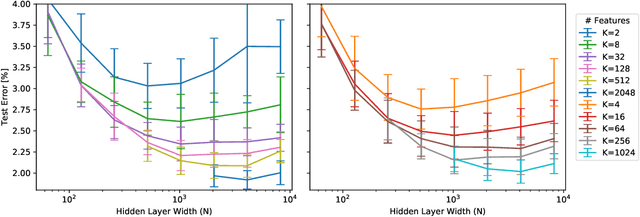
Transferability of learned features between tasks can massively reduce the cost of training a neural network on a novel task. We investigate the effect of network width on learned features using activation atlases --- a visualization technique that captures features the entire hidden state responds to, as opposed to individual neurons alone. We find that, while individual neurons do not learn interpretable features in wide networks, groups of neurons do. In addition, the hidden state of a wide network contains more information about the inputs than that of a narrow network trained to the same test accuracy. Inspired by this observation, we show that when fine-tuning the last layer of a network on a new task, performance improves significantly as the width of the network is increased, even though test accuracy on the original task is independent of width.