Amira Abbas
On quantum backpropagation, information reuse, and cheating measurement collapse
May 22, 2023

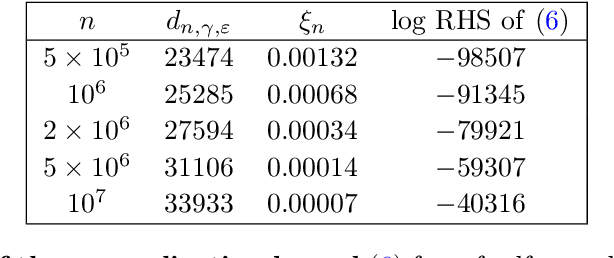
Abstract:The success of modern deep learning hinges on the ability to train neural networks at scale. Through clever reuse of intermediate information, backpropagation facilitates training through gradient computation at a total cost roughly proportional to running the function, rather than incurring an additional factor proportional to the number of parameters - which can now be in the trillions. Naively, one expects that quantum measurement collapse entirely rules out the reuse of quantum information as in backpropagation. But recent developments in shadow tomography, which assumes access to multiple copies of a quantum state, have challenged that notion. Here, we investigate whether parameterized quantum models can train as efficiently as classical neural networks. We show that achieving backpropagation scaling is impossible without access to multiple copies of a state. With this added ability, we introduce an algorithm with foundations in shadow tomography that matches backpropagation scaling in quantum resources while reducing classical auxiliary computational costs to open problems in shadow tomography. These results highlight the nuance of reusing quantum information for practical purposes and clarify the unique difficulties in training large quantum models, which could alter the course of quantum machine learning.
Effective dimension of machine learning models
Dec 09, 2021
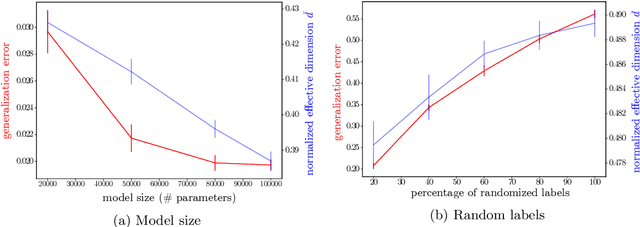
Abstract:Making statements about the performance of trained models on tasks involving new data is one of the primary goals of machine learning, i.e., to understand the generalization power of a model. Various capacity measures try to capture this ability, but usually fall short in explaining important characteristics of models that we observe in practice. In this study, we propose the local effective dimension as a capacity measure which seems to correlate well with generalization error on standard data sets. Importantly, we prove that the local effective dimension bounds the generalization error and discuss the aptness of this capacity measure for machine learning models.
The power of quantum neural networks
Oct 30, 2020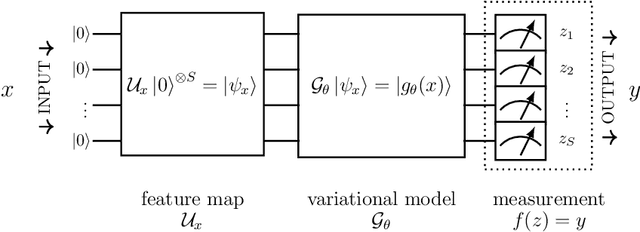
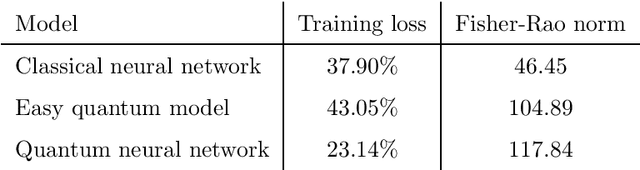
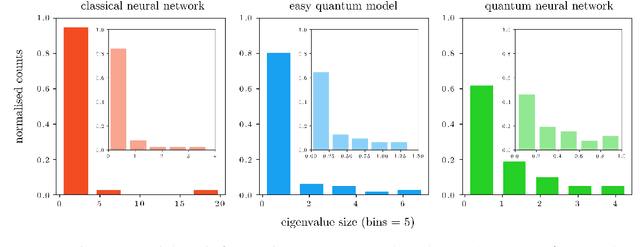
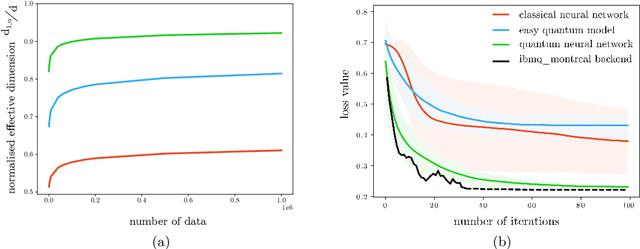
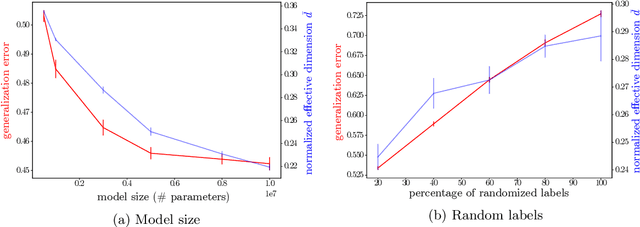
Abstract:Fault-tolerant quantum computers offer the promise of dramatically improving machine learning through speed-ups in computation or improved model scalability. In the near-term, however, the benefits of quantum machine learning are not so clear. Understanding expressibility and trainability of quantum models-and quantum neural networks in particular-requires further investigation. In this work, we use tools from information geometry to define a notion of expressibility for quantum and classical models. The effective dimension, which depends on the Fisher information, is used to prove a novel generalisation bound and establish a robust measure of expressibility. We show that quantum neural networks are able to achieve a significantly better effective dimension than comparable classical neural networks. To then assess the trainability of quantum models, we connect the Fisher information spectrum to barren plateaus, the problem of vanishing gradients. Importantly, certain quantum neural networks can show resilience to this phenomenon and train faster than classical models due to their favourable optimisation landscapes, captured by a more evenly spread Fisher information spectrum. Our work is the first to demonstrate that well-designed quantum neural networks offer an advantage over classical neural networks through a higher effective dimension and faster training ability, which we verify on real quantum hardware.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge