A Two-Scale Complexity Measure for Deep Learning Models

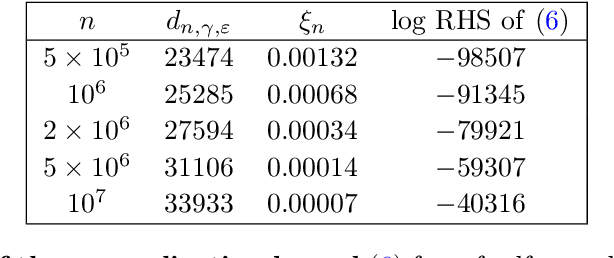
We introduce a novel capacity measure 2sED for statistical models based on the effective dimension. The new quantity provably bounds the generalization error under mild assumptions on the model. Furthermore, simulations on standard data sets and popular model architectures show that 2sED correlates well with the training error. For Markovian models, we show how to efficiently approximate 2sED from below through a layerwise iterative approach, which allows us to tackle deep learning models with a large number of parameters. Simulation results suggest that the approximation is good for different prominent models and data sets.

Infinite-width limit of deep linear neural networks

This paper studies the infinite-width limit of deep linear neural networks initialized with random parameters. We obtain that, when the number of neurons diverges, the training dynamics converge (in a precise sense) to the dynamics obtained from a gradient descent on an infinitely wide deterministic linear neural network. Moreover, even if the weights remain random, we get their precise law along the training dynamics, and prove a quantitative convergence result of the linear predictor in terms of the number of neurons. We finally study the continuous-time limit obtained for infinitely wide linear neural networks and show that the linear predictors of the neural network converge at an exponential rate to the minimal $\ell_2$-norm minimizer of the risk.

Effective dimension of machine learning models

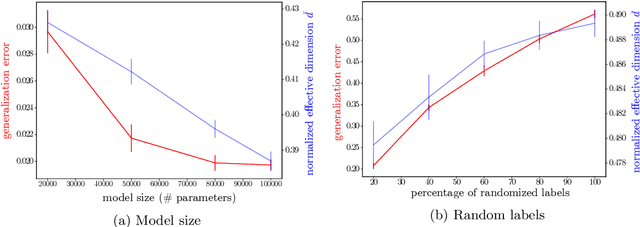
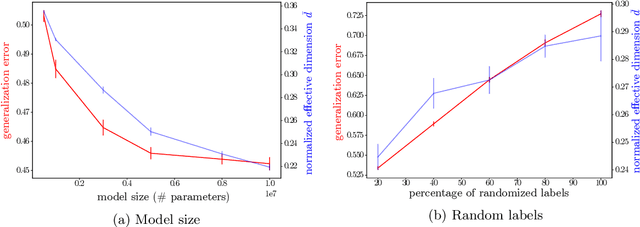
Making statements about the performance of trained models on tasks involving new data is one of the primary goals of machine learning, i.e., to understand the generalization power of a model. Various capacity measures try to capture this ability, but usually fall short in explaining important characteristics of models that we observe in practice. In this study, we propose the local effective dimension as a capacity measure which seems to correlate well with generalization error on standard data sets. Importantly, we prove that the local effective dimension bounds the generalization error and discuss the aptness of this capacity measure for machine learning models.

The power of quantum neural networks

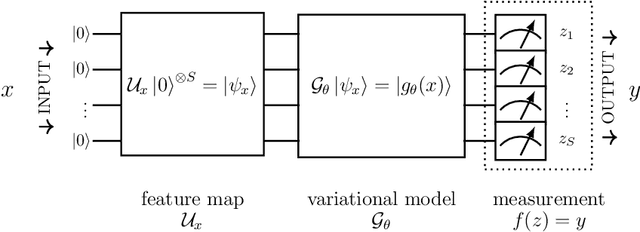
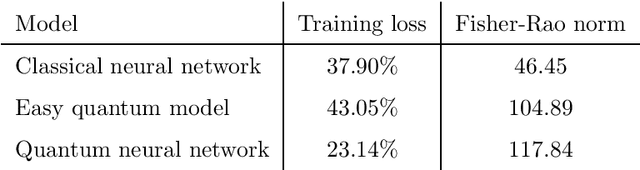
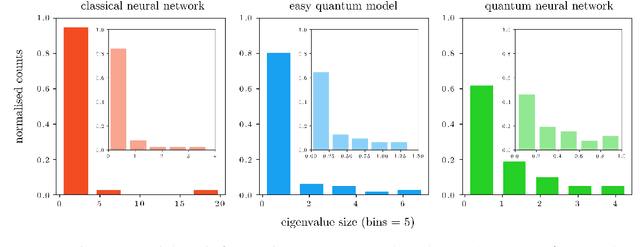
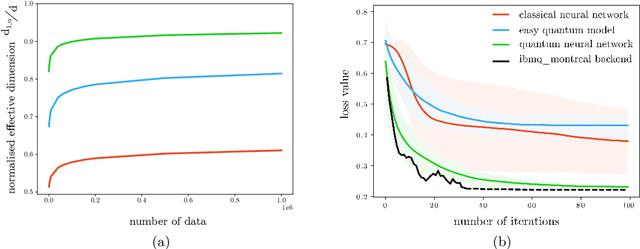
Fault-tolerant quantum computers offer the promise of dramatically improving machine learning through speed-ups in computation or improved model scalability. In the near-term, however, the benefits of quantum machine learning are not so clear. Understanding expressibility and trainability of quantum models-and quantum neural networks in particular-requires further investigation. In this work, we use tools from information geometry to define a notion of expressibility for quantum and classical models. The effective dimension, which depends on the Fisher information, is used to prove a novel generalisation bound and establish a robust measure of expressibility. We show that quantum neural networks are able to achieve a significantly better effective dimension than comparable classical neural networks. To then assess the trainability of quantum models, we connect the Fisher information spectrum to barren plateaus, the problem of vanishing gradients. Importantly, certain quantum neural networks can show resilience to this phenomenon and train faster than classical models due to their favourable optimisation landscapes, captured by a more evenly spread Fisher information spectrum. Our work is the first to demonstrate that well-designed quantum neural networks offer an advantage over classical neural networks through a higher effective dimension and faster training ability, which we verify on real quantum hardware.

A scale-dependent notion of effective dimension

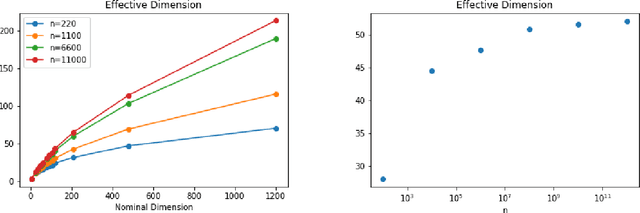
We introduce a notion of "effective dimension" of a statistical model based on the number of cubes of size $1/\sqrt{n}$ needed to cover the model space when endowed with the Fisher Information Matrix as metric, $n$ being the number of observations. The number of observations fixes a natural scale or resolution. The effective dimension is then measured via the spectrum of the Fisher Information Matrix regularized using this natural scale.