A Two-Scale Complexity Measure for Deep Learning Models

We introduce a novel capacity measure 2sED for statistical models based on the effective dimension. The new quantity provably bounds the generalization error under mild assumptions on the model. Furthermore, simulations on standard data sets and popular model architectures show that 2sED correlates well with the training error. For Markovian models, we show how to efficiently approximate 2sED from below through a layerwise iterative approach, which allows us to tackle deep learning models with a large number of parameters. Simulation results suggest that the approximation is good for different prominent models and data sets.

Training Quantised Neural Networks with STE Variants: the Additive Noise Annealing Algorithm

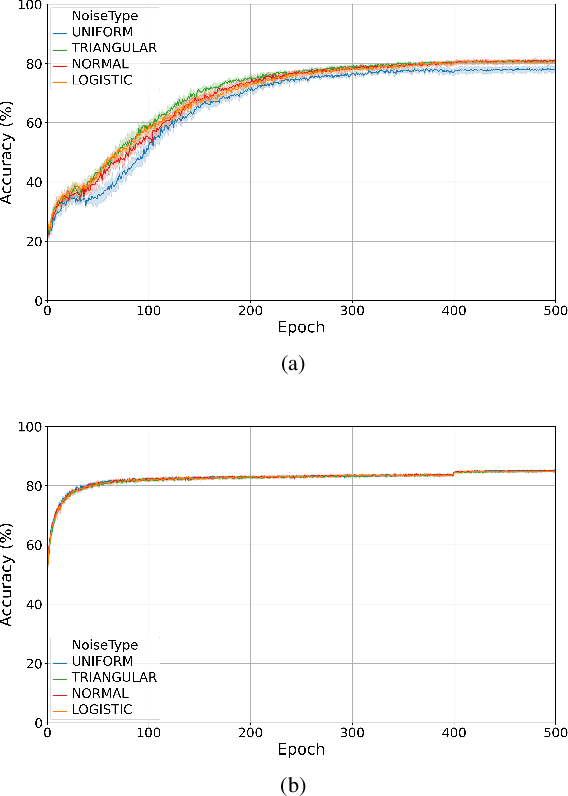
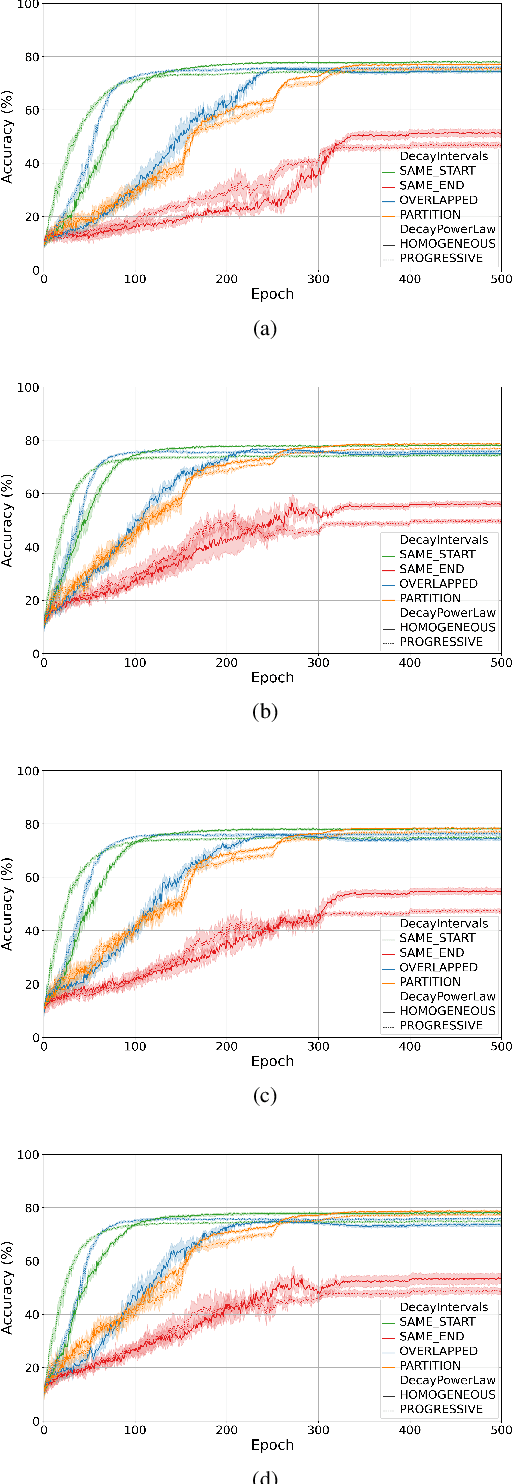
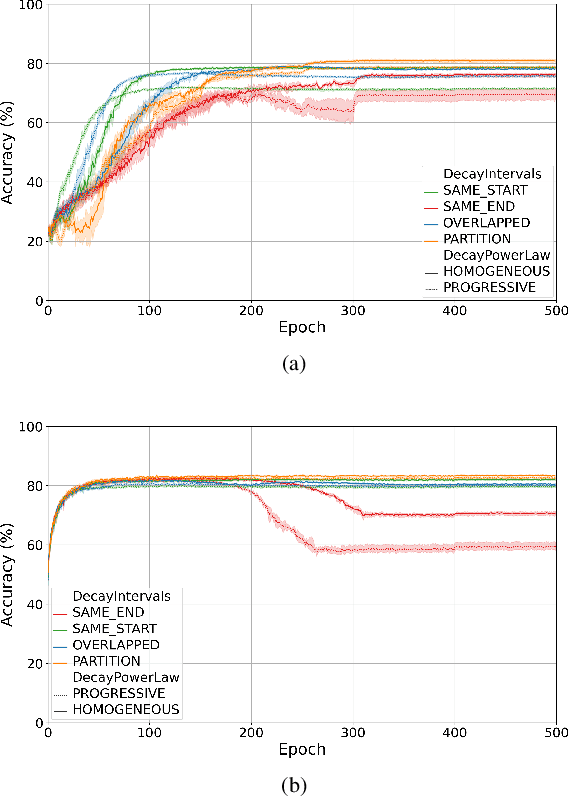
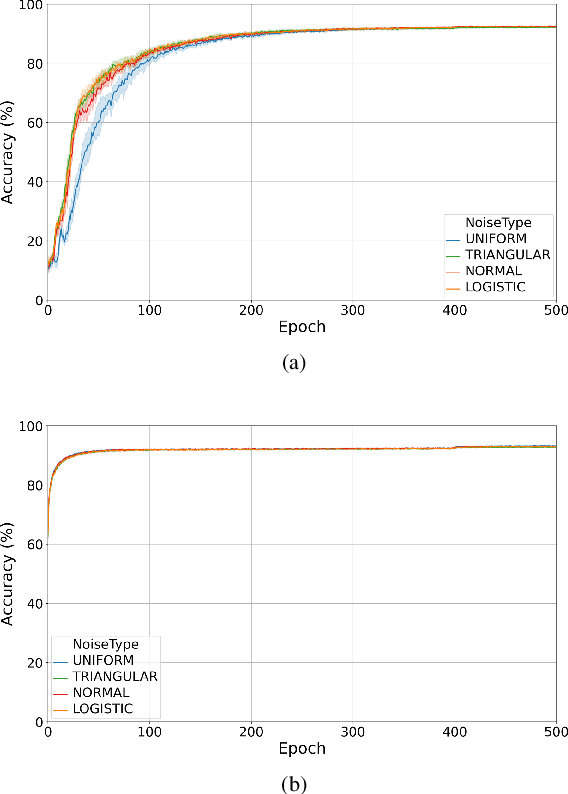
Training quantised neural networks (QNNs) is a non-differentiable optimisation problem since weights and features are output by piecewise constant functions. The standard solution is to apply the straight-through estimator (STE), using different functions during the inference and gradient computation steps. Several STE variants have been proposed in the literature aiming to maximise the task accuracy of the trained network. In this paper, we analyse STE variants and study their impact on QNN training. We first observe that most such variants can be modelled as stochastic regularisations of stair functions; although this intuitive interpretation is not new, our rigorous discussion generalises to further variants. Then, we analyse QNNs mixing different regularisations, finding that some suitably synchronised smoothing of each layer map is required to guarantee pointwise compositional convergence to the target discontinuous function. Based on these theoretical insights, we propose additive noise annealing (ANA), a new algorithm to train QNNs encompassing standard STE and its variants as special cases. When testing ANA on the CIFAR-10 image classification benchmark, we find that the major impact on task accuracy is not due to the qualitative shape of the regularisations but to the proper synchronisation of the different STE variants used in a network, in accordance with the theoretical results.

Analytical aspects of non-differentiable neural networks

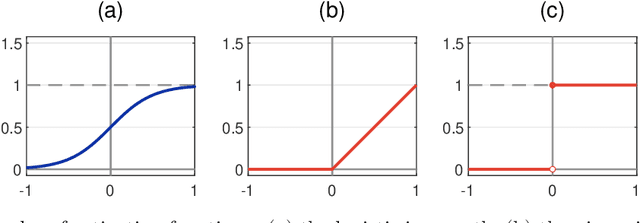
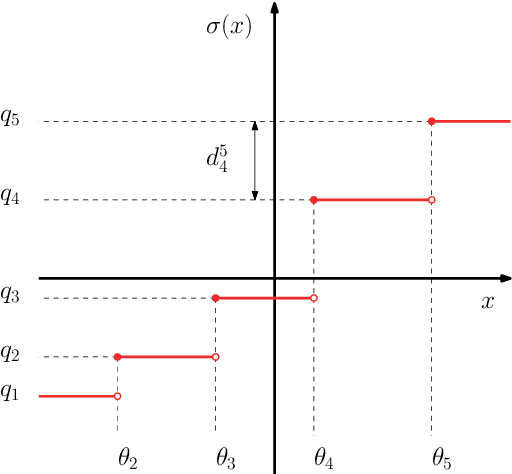
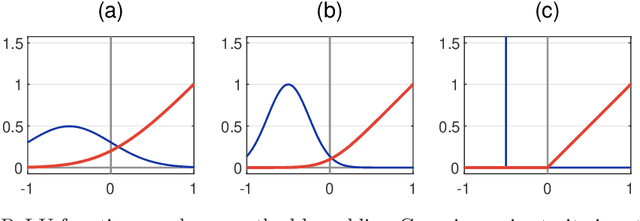
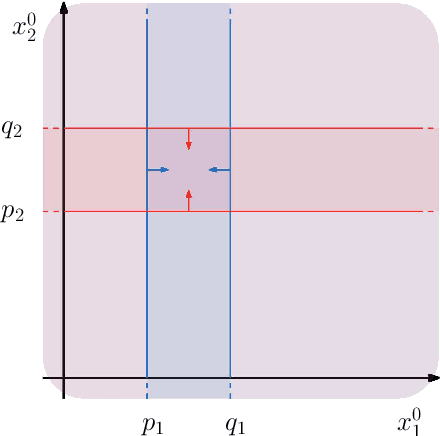
Research in computational deep learning has directed considerable efforts towards hardware-oriented optimisations for deep neural networks, via the simplification of the activation functions, or the quantization of both activations and weights. The resulting non-differentiability (or even discontinuity) of the networks poses some challenging problems, especially in connection with the learning process. In this paper, we address several questions regarding both the expressivity of quantized neural networks and approximation techniques for non-differentiable networks. First, we answer in the affirmative the question of whether QNNs have the same expressivity as DNNs in terms of approximation of Lipschitz functions in the $L^{\infty}$ norm. Then, considering a continuous but not necessarily differentiable network, we describe a layer-wise stochastic regularisation technique to produce differentiable approximations, and we show how this approach to regularisation provides elegant quantitative estimates. Finally, we consider networks defined by means of Heaviside-type activation functions, and prove for them a pointwise approximation result by means of smooth networks under suitable assumptions on the regularised activations.

Additive Noise Annealing and Approximation Properties of Quantized Neural Networks

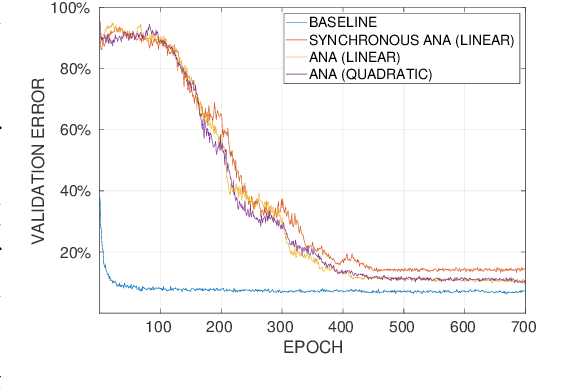
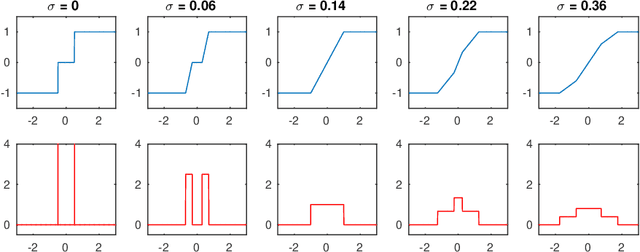
We present a theoretical and experimental investigation of the quantization problem for artificial neural networks. We provide a mathematical definition of quantized neural networks and analyze their approximation capabilities, showing in particular that any Lipschitz-continuous map defined on a hypercube can be uniformly approximated by a quantized neural network. We then focus on the regularization effect of additive noise on the arguments of multi-step functions inherent to the quantization of continuous variables. In particular, when the expectation operator is applied to a non-differentiable multi-step random function, and if the underlying probability density is differentiable (in either classical or weak sense), then a differentiable function is retrieved, with explicit bounds on its Lipschitz constant. Based on these results, we propose a novel gradient-based training algorithm for quantized neural networks that generalizes the straight-through estimator, acting on noise applied to the network's parameters. We evaluate our algorithm on the CIFAR-10 and ImageNet image classification benchmarks, showing state-of-the-art performance on AlexNet and MobileNetV2 for ternary networks.