A Two-Scale Complexity Measure for Deep Learning Models

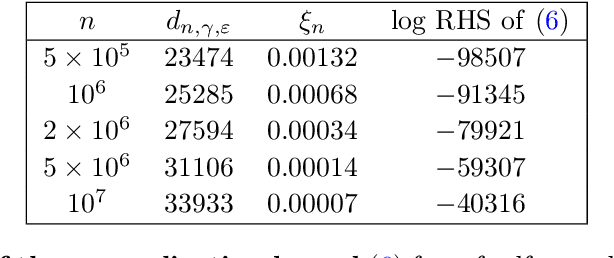
We introduce a novel capacity measure 2sED for statistical models based on the effective dimension. The new quantity provably bounds the generalization error under mild assumptions on the model. Furthermore, simulations on standard data sets and popular model architectures show that 2sED correlates well with the training error. For Markovian models, we show how to efficiently approximate 2sED from below through a layerwise iterative approach, which allows us to tackle deep learning models with a large number of parameters. Simulation results suggest that the approximation is good for different prominent models and data sets.

Quantum Kernel Alignment with Stochastic Gradient Descent

Quantum support vector machines have the potential to achieve a quantum speedup for solving certain machine learning problems. The key challenge for doing so is finding good quantum kernels for a given data set -- a task called kernel alignment. In this paper we study this problem using the Pegasos algorithm, which is an algorithm that uses stochastic gradient descent to solve the support vector machine optimization problem. We extend Pegasos to the quantum case and and demonstrate its effectiveness for kernel alignment. Unlike previous work which performs kernel alignment by training a QSVM within an outer optimization loop, we show that using Pegasos it is possible to simultaneously train the support vector machine and align the kernel. Our experiments show that this approach is capable of aligning quantum feature maps with high accuracy, and outperforms existing quantum kernel alignment techniques. Specifically, we demonstrate that Pegasos is particularly effective for non-stationary data, which is an important challenge in real-world applications.

The complexity of quantum support vector machines

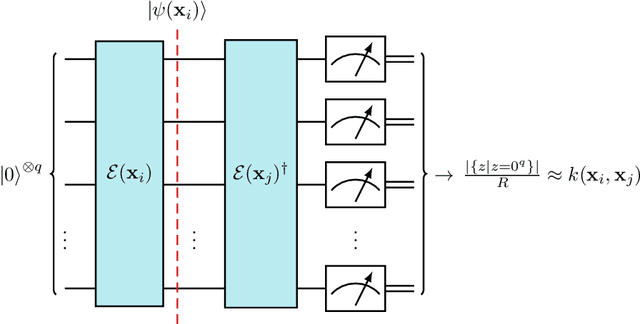
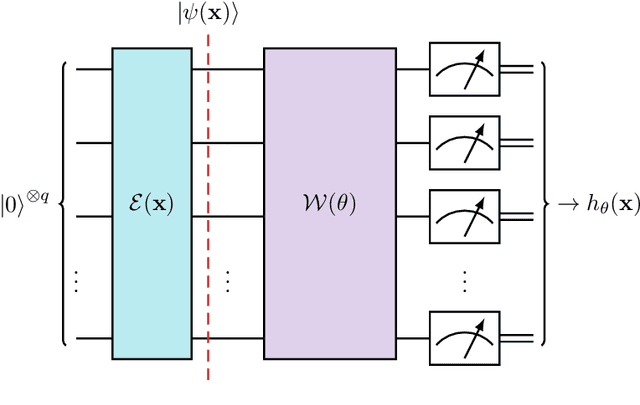
Quantum support vector machines employ quantum circuits to define the kernel function. It has been shown that this approach offers a provable exponential speedup compared to any known classical algorithm for certain data sets. The training of such models corresponds to solving a convex optimization problem either via its primal or dual formulation. Due to the probabilistic nature of quantum mechanics, the training algorithms are affected by statistical uncertainty, which has a major impact on their complexity. We show that the dual problem can be solved in $\mathcal{O}(M^{4.67}/\varepsilon^2)$ quantum circuit evaluations, where $M$ denotes the size of the data set and $\varepsilon$ the solution accuracy. We prove under an empirically motivated assumption that the kernelized primal problem can alternatively be solved in $\mathcal{O}(\min \{ M^2/\varepsilon^6, \, 1/\varepsilon^{10} \})$ evaluations by employing a generalization of a known classical algorithm called Pegasos. Accompanying empirical results demonstrate these analytical complexities to be essentially tight. In addition, we investigate a variational approximation to quantum support vector machines and show that their heuristic training achieves considerably better scaling in our experiments.

Effective dimension of machine learning models

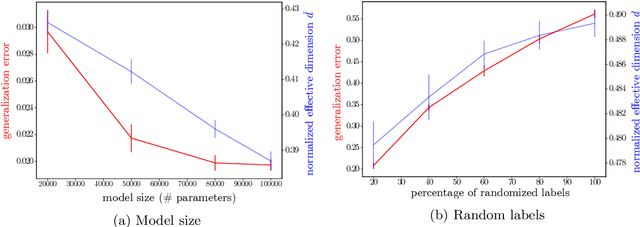
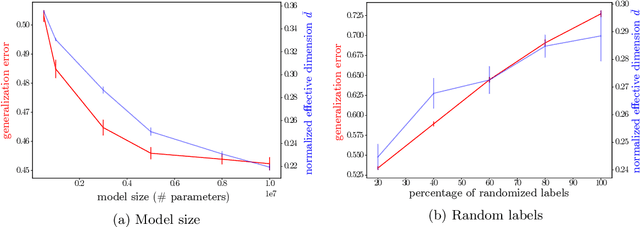
Making statements about the performance of trained models on tasks involving new data is one of the primary goals of machine learning, i.e., to understand the generalization power of a model. Various capacity measures try to capture this ability, but usually fall short in explaining important characteristics of models that we observe in practice. In this study, we propose the local effective dimension as a capacity measure which seems to correlate well with generalization error on standard data sets. Importantly, we prove that the local effective dimension bounds the generalization error and discuss the aptness of this capacity measure for machine learning models.

The power of quantum neural networks

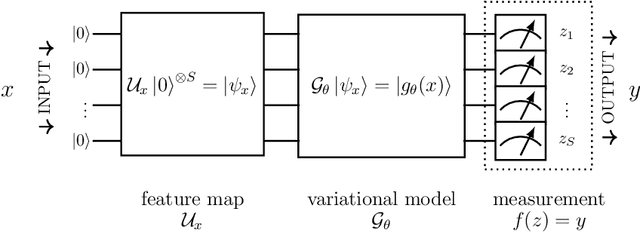
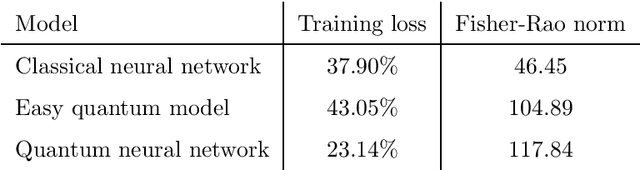
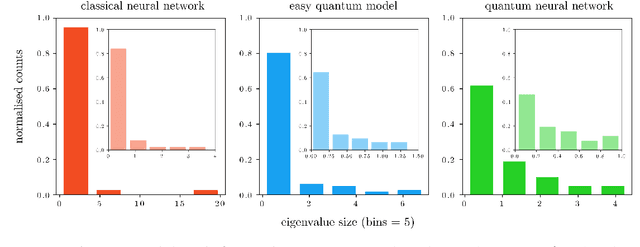
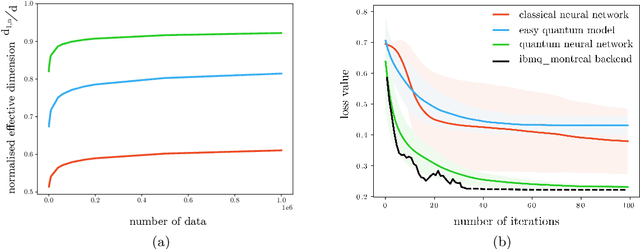
Fault-tolerant quantum computers offer the promise of dramatically improving machine learning through speed-ups in computation or improved model scalability. In the near-term, however, the benefits of quantum machine learning are not so clear. Understanding expressibility and trainability of quantum models-and quantum neural networks in particular-requires further investigation. In this work, we use tools from information geometry to define a notion of expressibility for quantum and classical models. The effective dimension, which depends on the Fisher information, is used to prove a novel generalisation bound and establish a robust measure of expressibility. We show that quantum neural networks are able to achieve a significantly better effective dimension than comparable classical neural networks. To then assess the trainability of quantum models, we connect the Fisher information spectrum to barren plateaus, the problem of vanishing gradients. Importantly, certain quantum neural networks can show resilience to this phenomenon and train faster than classical models due to their favourable optimisation landscapes, captured by a more evenly spread Fisher information spectrum. Our work is the first to demonstrate that well-designed quantum neural networks offer an advantage over classical neural networks through a higher effective dimension and faster training ability, which we verify on real quantum hardware.

Generalized maximum entropy estimation

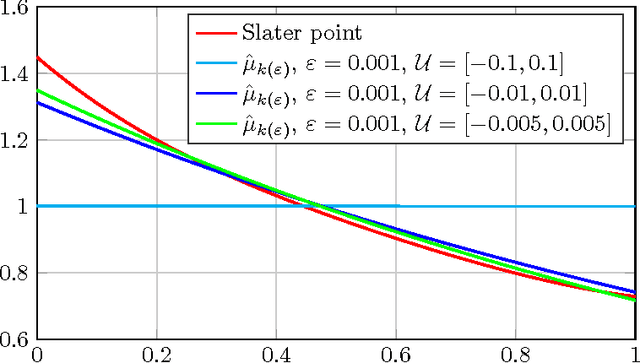
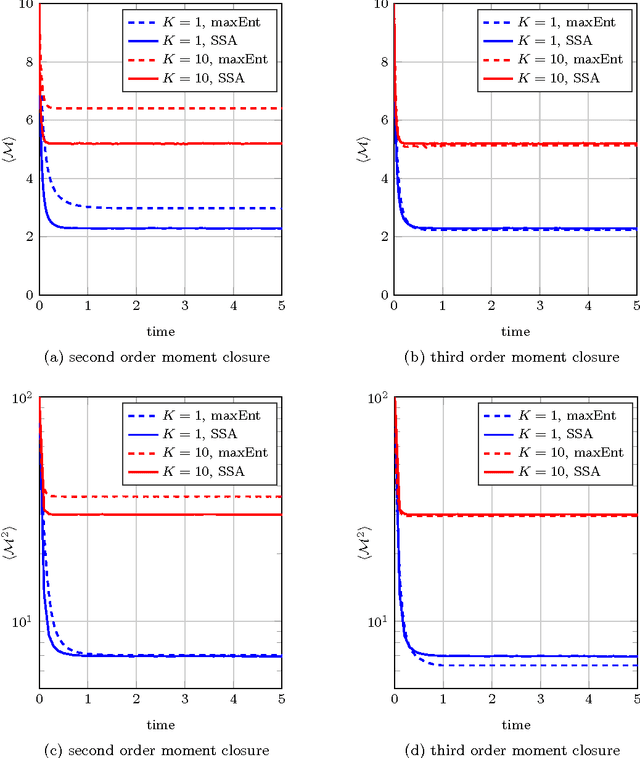
We consider the problem of estimating a probability distribution that maximizes the entropy while satisfying a finite number of moment constraints, possibly corrupted by noise. Based on duality of convex programming, we present a novel approximation scheme using a smoothed fast gradient method that is equipped with explicit bounds on the approximation error. We further demonstrate how the presented scheme can be used for approximating the chemical master equation through the zero-information moment closure method.