Quantum Kernel Alignment with Stochastic Gradient Descent

Quantum support vector machines have the potential to achieve a quantum speedup for solving certain machine learning problems. The key challenge for doing so is finding good quantum kernels for a given data set -- a task called kernel alignment. In this paper we study this problem using the Pegasos algorithm, which is an algorithm that uses stochastic gradient descent to solve the support vector machine optimization problem. We extend Pegasos to the quantum case and and demonstrate its effectiveness for kernel alignment. Unlike previous work which performs kernel alignment by training a QSVM within an outer optimization loop, we show that using Pegasos it is possible to simultaneously train the support vector machine and align the kernel. Our experiments show that this approach is capable of aligning quantum feature maps with high accuracy, and outperforms existing quantum kernel alignment techniques. Specifically, we demonstrate that Pegasos is particularly effective for non-stationary data, which is an important challenge in real-world applications.

The complexity of quantum support vector machines

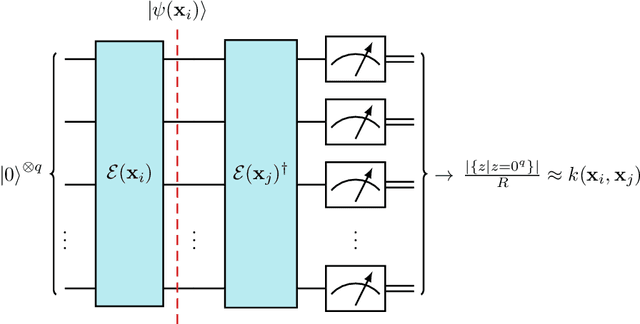
Quantum support vector machines employ quantum circuits to define the kernel function. It has been shown that this approach offers a provable exponential speedup compared to any known classical algorithm for certain data sets. The training of such models corresponds to solving a convex optimization problem either via its primal or dual formulation. Due to the probabilistic nature of quantum mechanics, the training algorithms are affected by statistical uncertainty, which has a major impact on their complexity. We show that the dual problem can be solved in $\mathcal{O}(M^{4.67}/\varepsilon^2)$ quantum circuit evaluations, where $M$ denotes the size of the data set and $\varepsilon$ the solution accuracy. We prove under an empirically motivated assumption that the kernelized primal problem can alternatively be solved in $\mathcal{O}(\min \{ M^2/\varepsilon^6, \, 1/\varepsilon^{10} \})$ evaluations by employing a generalization of a known classical algorithm called Pegasos. Accompanying empirical results demonstrate these analytical complexities to be essentially tight. In addition, we investigate a variational approximation to quantum support vector machines and show that their heuristic training achieves considerably better scaling in our experiments.