Nonlinear Estimator: Dual Bayesian Affine Estimators for Parameter Learning

This paper presents a nonlinear parameter estimator for Wiener-type state-space models obtained as a fixed-point architecture that couples two affine minimum mean-squared error (MMSE) estimators: one for the unknown parameters and one for latent variables. The architecture retains the functional structure of the optimal affine MMSE parameter estimator while incorporating Dynamic Basis Statistics (DBS) estimates that summarize nonlinear basis-function evaluations. Two DBS construction strategies are developed, leading to two nonlinear estimator frameworks. The dual basis-parameter estimator combines an affine basis estimator with the affine parameter estimator, whereas the dual state-parameter estimator first computes affine state estimates and their covariances, then maps these state-estimate statistics through a Gaussian DBS operator to obtain DBS estimates. Both dual estimators admit fixed-point characterizations that alternate between estimating each component using the updated prior of the other, obtained from that component's plug-in estimate statistics from the previous iteration. The efficacy of the proposed methods is examined via extensive Monte Carlo experiments, showing that the dual basis-parameter estimator attains parameter mean-squared errors comparable to those of the purely affine parameter estimator, while the dual state-parameter estimator achieves the lowest parameter mean-squared error, outperforming both the dual basis-parameter and purely affine parameter estimators, as well as sequential Monte Carlo variants of classical Particle Gibbs and Expectation-Maximization schemes.

Rate or Fate? RLV$^\varepsilon$R: Reinforcement Learning with Verifiable Noisy Rewards

Reinforcement learning with verifiable rewards (RLVR) is a simple but powerful paradigm for training LLMs: sample a completion, verify it, and update. In practice, however, the verifier is almost never clean--unit tests probe only limited corner cases; human and synthetic labels are imperfect; and LLM judges (e.g., RLAIF) are noisy and can be exploited--and this problem worsens on harder domains (especially coding) where tests are sparse and increasingly model-generated. We ask a pragmatic question: does the verification noise merely slow down the learning (rate), or can it flip the outcome (fate)? To address this, we develop an analytically tractable multi-armed bandit view of RLVR dynamics, instantiated with GRPO and validated in controlled experiments. Modeling false positives and false negatives and grouping completions into recurring reasoning modes yields a replicator-style (natural-selection) flow on the probability simplex. The dynamics decouples into within-correct-mode competition and a one-dimensional evolution for the mass on incorrect modes, whose drift is determined solely by Youden's index J=TPR-FPR. This yields a sharp phase transition: when J>0, the incorrect mass is driven toward extinction (learning); when J=0, the process is neutral; and when J<0, incorrect modes amplify until they dominate (anti-learning and collapse). In the learning regime J>0, noise primarily rescales convergence time ("rate, not fate"). Experiments on verifiable programming tasks under synthetic noise reproduce the predicted J=0 boundary. Beyond noise, the framework offers a general lens for analyzing RLVR stability, convergence, and algorithmic interventions.

Rank-One Modified Value Iteration

In this paper, we provide a novel algorithm for solving planning and learning problems of Markov decision processes. The proposed algorithm follows a policy iteration-type update by using a rank-one approximation of the transition probability matrix in the policy evaluation step. This rank-one approximation is closely related to the stationary distribution of the corresponding transition probability matrix, which is approximated using the power method. We provide theoretical guarantees for the convergence of the proposed algorithm to optimal (action-)value function with the same rate and computational complexity as the value iteration algorithm in the planning problem and as the Q-learning algorithm in the learning problem. Through our extensive numerical simulations, however, we show that the proposed algorithm consistently outperforms first-order algorithms and their accelerated versions for both planning and learning problems.

Optimal Bayesian Affine Estimator and Active Learning for the Wiener Model

This paper presents a Bayesian estimation framework for Wiener models, focusing on learning nonlinear output functions under known linear state dynamics. We derive a closed-form optimal affine estimator for the unknown parameters, characterized by the so-called "dynamic basis statistics (DBS)." Several features of the proposed estimator are studied, including Bayesian unbiasedness, closed-form posterior statistics, error monotonicity in trajectory length, and consistency condition (also known as persistent excitation). In the special case of Fourier basis functions, we demonstrate that the closed-form description is computationally available, as the Fourier DBS enjoys explicit expression. Furthermore, we identify an inherent inconsistency in single-trajectory measurements, regardless of input excitation. Leveraging the closed-form estimation error, we develop an active learning algorithm synthesizing input signals to minimize estimation error. Numerical experiments validate the efficacy of our approach, showing significant improvements over traditional regularized least-squares methods.

Offline Reinforcement Learning via Inverse Optimization

Inspired by the recent successes of Inverse Optimization (IO) across various application domains, we propose a novel offline Reinforcement Learning (ORL) algorithm for continuous state and action spaces, leveraging the convex loss function called ``sub-optimality loss" from the IO literature. To mitigate the distribution shift commonly observed in ORL problems, we further employ a robust and non-causal Model Predictive Control (MPC) expert steering a nominal model of the dynamics using in-hindsight information stemming from the model mismatch. Unlike the existing literature, our robust MPC expert enjoys an exact and tractable convex reformulation. In the second part of this study, we show that the IO hypothesis class, trained by the proposed convex loss function, enjoys ample expressiveness and achieves competitive performance comparing with the state-of-the-art (SOTA) methods in the low-data regime of the MuJoCo benchmark while utilizing three orders of magnitude fewer parameters, thereby requiring significantly fewer computational resources. To facilitate the reproducibility of our results, we provide an open-source package implementing the proposed algorithms and the experiments.

Scalable Kernel Inverse Optimization

Inverse Optimization (IO) is a framework for learning the unknown objective function of an expert decision-maker from a past dataset. In this paper, we extend the hypothesis class of IO objective functions to a reproducing kernel Hilbert space (RKHS), thereby enhancing feature representation to an infinite-dimensional space. We demonstrate that a variant of the representer theorem holds for a specific training loss, allowing the reformulation of the problem as a finite-dimensional convex optimization program. To address scalability issues commonly associated with kernel methods, we propose the Sequential Selection Optimization (SSO) algorithm to efficiently train the proposed Kernel Inverse Optimization (KIO) model. Finally, we validate the generalization capabilities of the proposed KIO model and the effectiveness of the SSO algorithm through learning-from-demonstration tasks on the MuJoCo benchmark.

Variance-Reduced Cascade Q-learning: Algorithms and Sample Complexity

We study the problem of estimating the optimal Q-function of $\gamma$-discounted Markov decision processes (MDPs) under the synchronous setting, where independent samples for all state-action pairs are drawn from a generative model at each iteration. We introduce and analyze a novel model-free algorithm called Variance-Reduced Cascade Q-learning (VRCQ). VRCQ comprises two key building blocks: (i) the established direct variance reduction technique and (ii) our proposed variance reduction scheme, Cascade Q-learning. By leveraging these techniques, VRCQ provides superior guarantees in the $\ell_\infty$-norm compared with the existing model-free stochastic approximation-type algorithms. Specifically, we demonstrate that VRCQ is minimax optimal. Additionally, when the action set is a singleton (so that the Q-learning problem reduces to policy evaluation), it achieves non-asymptotic instance optimality while requiring the minimum number of samples theoretically possible. Our theoretical results and their practical implications are supported by numerical experiments.

From Optimization to Control: Quasi Policy Iteration

Recent control algorithms for Markov decision processes (MDPs) have been designed using an implicit analogy with well-established optimization algorithms. In this paper, we make this analogy explicit across four problem classes with a unified solution characterization. This novel framework, in turn, allows for a systematic transformation of algorithms from one domain to the other. In particular, we identify equivalent optimization and control algorithms that have already been pointed out in the existing literature, but mostly in a scattered way. With this unifying framework in mind, we then exploit two linear structural constraints specific to MDPs for approximating the Hessian in a second-order-type algorithm from optimization, namely, Anderson mixing. This leads to a novel first-order control algorithm that modifies the standard value iteration (VI) algorithm by incorporating two new directions and adaptive step sizes. While the proposed algorithm, coined as quasi-policy iteration, has the same computational complexity as VI, it interestingly exhibits an empirical convergence behavior similar to policy iteration with a very low sensitivity to the discount factor.

Inverse Optimization for Routing Problems

We propose a method for learning decision-makers' behavior in routing problems using Inverse Optimization (IO). The IO framework falls into the supervised learning category and builds on the premise that the target behavior is an optimizer of an unknown cost function. This cost function is to be learned through historical data, and in the context of routing problems, can be interpreted as the routing preferences of the decision-makers. In this view, the main contributions of this study are to propose an IO methodology with a hypothesis function, loss function, and stochastic first-order algorithm tailored to routing problems. We further test our IO approach in the Amazon Last Mile Routing Research Challenge, where the goal is to learn models that replicate the routing preferences of human drivers, using thousands of real-world routing examples. Our final IO-learned routing model achieves a score that ranks 2nd compared with the 48 models that qualified for the final round of the challenge. Our results showcase the flexibility and real-world potential of the proposed IO methodology to learn from decision-makers' decisions in routing problems.

Nonlinear Distributionally Robust Optimization

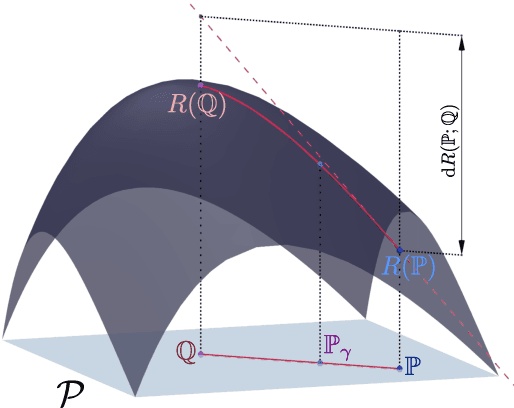
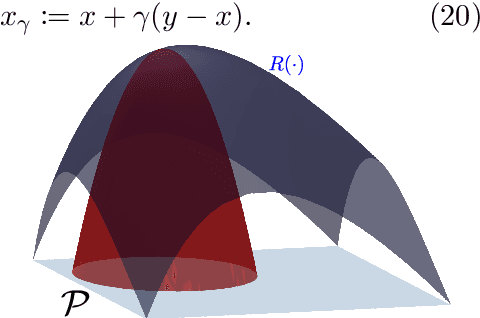
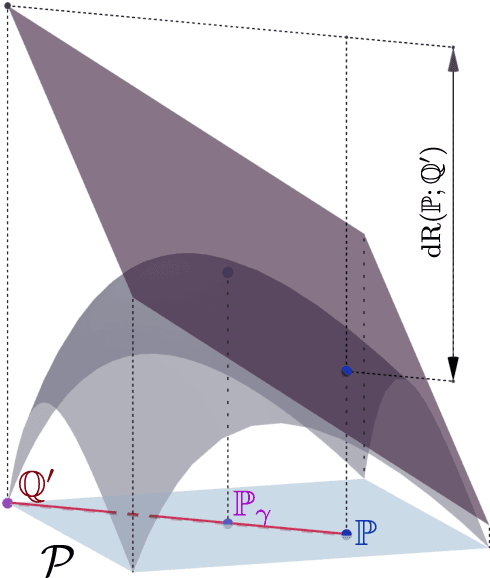
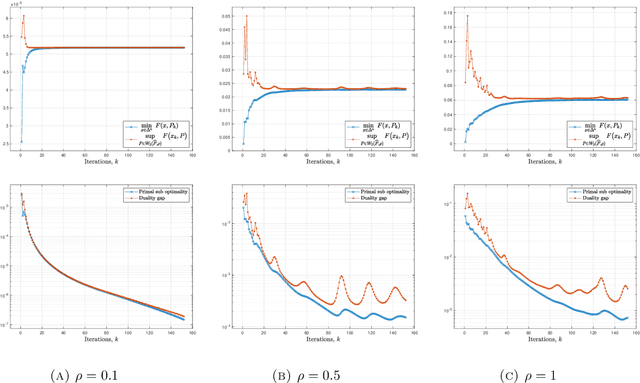
This article focuses on a class of distributionally robust optimization (DRO) problems where, unlike the growing body of the literature, the objective function is potentially non-linear in the distribution. Existing methods to optimize nonlinear functions in probability space use the Frechet derivatives, which present both theoretical and computational challenges. Motivated by this, we propose an alternative notion for the derivative and corresponding smoothness based on Gateaux (G)-derivative for generic risk measures. These concepts are explained via three running risk measure examples of variance, entropic risk, and risk on finite support sets. We then propose a G-derivative based Frank-Wolfe~(FW) algorithm for generic non-linear optimization problems in probability spaces and establish its convergence under the proposed notion of smoothness in a completely norm-independent manner. We use the set-up of the FW algorithm to devise a methodology to compute a saddle point of the non-linear DRO problem. Finally, for the minimum variance portfolio selection problem we analyze the regularity conditions and compute the FW-oracle in various settings, and validate the theoretical results numerically.