Nonlinear Distributionally Robust Optimization

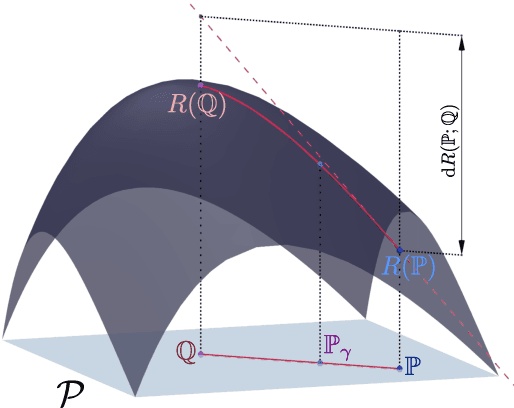
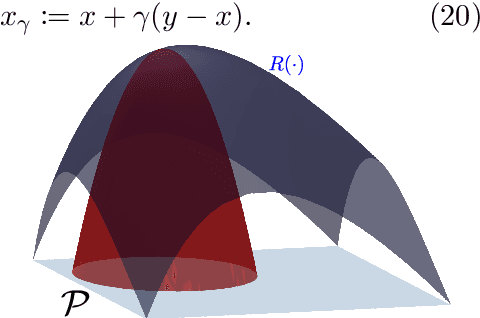
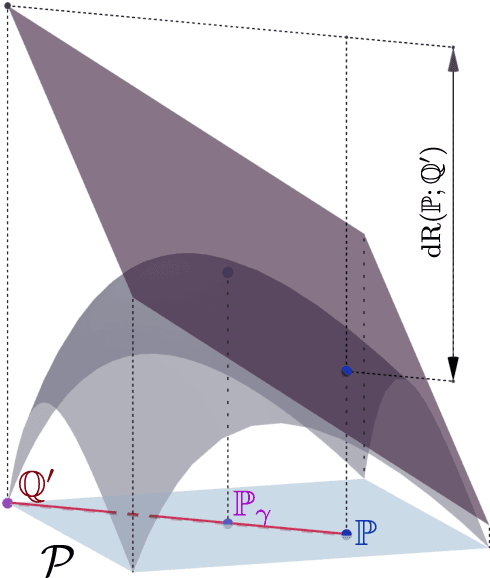
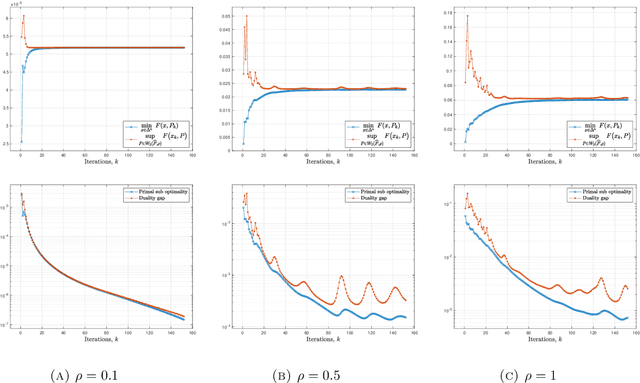
This article focuses on a class of distributionally robust optimization (DRO) problems where, unlike the growing body of the literature, the objective function is potentially non-linear in the distribution. Existing methods to optimize nonlinear functions in probability space use the Frechet derivatives, which present both theoretical and computational challenges. Motivated by this, we propose an alternative notion for the derivative and corresponding smoothness based on Gateaux (G)-derivative for generic risk measures. These concepts are explained via three running risk measure examples of variance, entropic risk, and risk on finite support sets. We then propose a G-derivative based Frank-Wolfe~(FW) algorithm for generic non-linear optimization problems in probability spaces and establish its convergence under the proposed notion of smoothness in a completely norm-independent manner. We use the set-up of the FW algorithm to devise a methodology to compute a saddle point of the non-linear DRO problem. Finally, for the minimum variance portfolio selection problem we analyze the regularity conditions and compute the FW-oracle in various settings, and validate the theoretical results numerically.

Fast Algorithm for Constrained Linear Inverse Problems

We consider the constrained Linear Inverse Problem (LIP), where a certain atomic norm (like the $\ell_1 $ and the Nuclear norm) is minimized subject to a quadratic constraint. Typically, such cost functions are non-differentiable which makes them not amenable to the fast optimization methods existing in practice. We propose two equivalent reformulations of the constrained LIP with improved convex regularity: (i) a smooth convex minimization problem, and (ii) a strongly convex min-max problem. These problems could be solved by applying existing acceleration based convex optimization methods which provide better $ O \big( \frac{1}{k^2} \big) $ theoretical convergence guarantee. However, to fully exploit the utility of these reformulations, we also provide a novel algorithm, to which we refer as the Fast Linear Inverse Problem Solver (FLIPS), that is tailored to solve the reformulation of the LIP. We demonstrate the performance of FLIPS on the sparse coding problem arising in image processing tasks. In this setting, we observe that FLIPS consistently outperforms the Chambolle-Pock and C-SALSA algorithms--two of the current best methods in the literature.

Novel min-max reformulations of Linear Inverse Problems

In this article, we dwell into the class of so-called ill-posed Linear Inverse Problems (LIP) which simply refers to the task of recovering the entire signal from its relatively few random linear measurements. Such problems arise in a variety of settings with applications ranging from medical image processing, recommender systems, etc. We propose a slightly generalized version of the error constrained linear inverse problem and obtain a novel and equivalent convex-concave min-max reformulation by providing an exposition to its convex geometry. Saddle points of the min-max problem are completely characterized in terms of a solution to the LIP, and vice versa. Applying simple saddle point seeking ascend-descent type algorithms to solve the min-max problems provides novel and simple algorithms to find a solution to the LIP. Moreover, the reformulation of an LIP as the min-max problem provided in this article is crucial in developing methods to solve the dictionary learning problem with almost sure recovery constraints.

Dictionary Learning with Almost Sure Error Constraints

A dictionary is a database of standard vectors, so that other vectors / signals are expressed as linear combinations of dictionary vectors, and the task of learning a dictionary for a given data is to find a good dictionary so that the representation of data points has desirable features. Dictionary learning and the related matrix factorization methods have gained significant prominence recently due to their applications in Wide variety of fields like machine learning, signal processing, statistics etc. In this article we study the dictionary learning problem for achieving desirable features in the representation of a given data with almost sure recovery constraints. We impose the constraint that every sample is reconstructed properly to within a predefined threshold. This problem formulation is more challenging than the conventional dictionary learning, which is done by minimizing a regularised cost function. We make use of the duality results for linear inverse problems to obtain an equivalent reformulation in the form of a convex-concave min-max problem. The resulting min-max problem is then solved using gradient descent-ascent like algorithms.

Convex geometry of the Coding problem for error constrained Dictionary Learning

In this article we expose the convex geometry of the class of coding problems that includes the likes of Basis Pursuit Denoising. We propose a novel reformulation of the coding problem as a convex-concave min-max problem. This particular reformulation not only provides a nontrivial method to update the dictionary in order to obtain better sparse representations with hard error constraints, but also gives further insights into the underlying geometry of the coding problem. Our results shed provide pointers to new ascent-descent type algorithms that could be used to solve the coding problem.

A complete characterization of optimal dictionaries for least squares representation

Dictionaries are collections of vectors used for representations of elements in Euclidean spaces. While recent research on optimal dictionaries is focussed on providing sparse (i.e., $\ell_0$-optimal,) representations, here we consider the problem of finding optimal dictionaries such that representations of samples of a random vector are optimal in an $\ell_2$-sense. For us, optimality of representation is equivalent to minimization of the average $\ell_2$-norm of the coefficients used to represent the random vector, with the lengths of the dictionary vectors being specified a priori. With the help of recent results on rank-$1$ decompositions of symmetric positive semidefinite matrices and the theory of majorization, we provide a complete characterization of $\ell_2$-optimal dictionaries. Our results are accompanied by polynomial time algorithms that construct $\ell_2$-optimal dictionaries from given data.

Optimal dictionary for least squares representation

Dictionaries are collections of vectors used for representations of random vectors in Euclidean spaces. Recent research on optimal dictionaries is focused on constructing dictionaries that offer sparse representations, i.e., $\ell_0$-optimal representations. Here we consider the problem of finding optimal dictionaries with which representations of samples of a random vector are optimal in an $\ell_2$-sense: optimality of representation is defined as attaining the minimal average $\ell_2$-norm of the coefficients used to represent the random vector. With the help of recent results on rank-$1$ decompositions of symmetric positive semidefinite matrices, we provide an explicit description of $\ell_2$-optimal dictionaries as well as their algorithmic constructions in polynomial time.