A numerical algorithm for attaining the Chebyshev bound in optimal learning

Given a compact subset of a Banach space, the Chebyshev center problem consists of finding a minimal circumscribing ball containing the set. In this article we establish a numerically tractable algorithm for solving the Chebyshev center problem in the context of optimal learning from a finite set of data points. For a hypothesis space realized as a compact but not necessarily convex subset of a finite-dimensional subspace of some underlying Banach space, this algorithm computes the Chebyshev radius and the Chebyshev center of the hypothesis space, thereby solving the problem of optimal recovery of functions from data. The algorithm itself is based on, and significantly extends, recent results for near-optimal solutions of convex semi-infinite problems by means of targeted sampling, and it is of independent interest. Several examples of numerical computations of Chebyshev centers are included in order to illustrate the effectiveness of the algorithm.

Cross apprenticeship learning framework: Properties and solution approaches

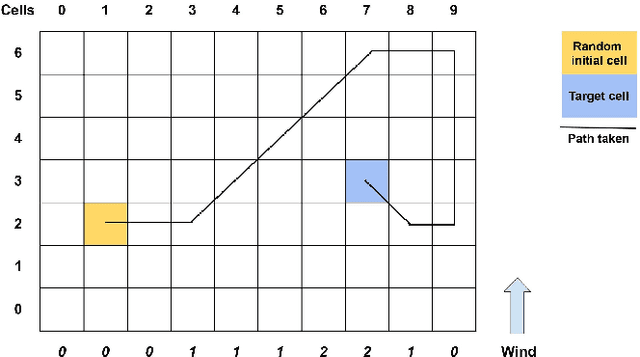
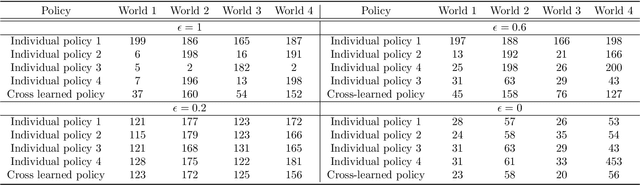
Apprenticeship learning is a framework in which an agent learns a policy to perform a given task in an environment using example trajectories provided by an expert. In the real world, one might have access to expert trajectories in different environments where the system dynamics is different while the learning task is the same. For such scenarios, two types of learning objectives can be defined. One where the learned policy performs very well in one specific environment and another when it performs well across all environments. To balance these two objectives in a principled way, our work presents the cross apprenticeship learning (CAL) framework. This consists of an optimization problem where an optimal policy for each environment is sought while ensuring that all policies remain close to each other. This nearness is facilitated by one tuning parameter in the optimization problem. We derive properties of the optimizers of the problem as the tuning parameter varies. Since the problem is nonconvex, we provide a convex outer approximation. Finally, we demonstrate the attributes of our framework in the context of a navigation task in a windy gridworld environment.

Novel min-max reformulations of Linear Inverse Problems

In this article, we dwell into the class of so-called ill-posed Linear Inverse Problems (LIP) which simply refers to the task of recovering the entire signal from its relatively few random linear measurements. Such problems arise in a variety of settings with applications ranging from medical image processing, recommender systems, etc. We propose a slightly generalized version of the error constrained linear inverse problem and obtain a novel and equivalent convex-concave min-max reformulation by providing an exposition to its convex geometry. Saddle points of the min-max problem are completely characterized in terms of a solution to the LIP, and vice versa. Applying simple saddle point seeking ascend-descent type algorithms to solve the min-max problems provides novel and simple algorithms to find a solution to the LIP. Moreover, the reformulation of an LIP as the min-max problem provided in this article is crucial in developing methods to solve the dictionary learning problem with almost sure recovery constraints.

Dictionary Learning with Almost Sure Error Constraints

A dictionary is a database of standard vectors, so that other vectors / signals are expressed as linear combinations of dictionary vectors, and the task of learning a dictionary for a given data is to find a good dictionary so that the representation of data points has desirable features. Dictionary learning and the related matrix factorization methods have gained significant prominence recently due to their applications in Wide variety of fields like machine learning, signal processing, statistics etc. In this article we study the dictionary learning problem for achieving desirable features in the representation of a given data with almost sure recovery constraints. We impose the constraint that every sample is reconstructed properly to within a predefined threshold. This problem formulation is more challenging than the conventional dictionary learning, which is done by minimizing a regularised cost function. We make use of the duality results for linear inverse problems to obtain an equivalent reformulation in the form of a convex-concave min-max problem. The resulting min-max problem is then solved using gradient descent-ascent like algorithms.

Convex geometry of the Coding problem for error constrained Dictionary Learning

In this article we expose the convex geometry of the class of coding problems that includes the likes of Basis Pursuit Denoising. We propose a novel reformulation of the coding problem as a convex-concave min-max problem. This particular reformulation not only provides a nontrivial method to update the dictionary in order to obtain better sparse representations with hard error constraints, but also gives further insights into the underlying geometry of the coding problem. Our results shed provide pointers to new ascent-descent type algorithms that could be used to solve the coding problem.

Scenario approach for minmax optimization with emphasis on the nonconvex case: positive results and caveats

We treat the so-called scenario approach, a popular probabilistic approximation method for robust minmax optimization problems via independent and indentically distributed (i.i.d) sampling from the uncertainty set, from various perspectives. The scenario approach is well-studied in the important case of convex robust optimization problems, and here we examine how the phenomenon of concentration of measures affects the i.i.d sampling aspect of the scenario approach in high dimensions and its relation with the optimal values. Moreover, we perform a detailed study of both the asymptotic behaviour (consistency) and finite time behaviour of the scenario approach in the more general setting of nonconvex minmax optimization problems. In the direction of the asymptotic behaviour of the scenario approach, we present an obstruction to consistency that arises when the decision set is noncompact. In the direction of finite sample guarantees, we establish a general methodology for extracting `probably approximately correct' type estimates for the finite sample behaviour of the scenario approach for a large class of nonconvex problems.

Structure-preserving constrained optimal trajectory planning of a wheeled inverted pendulum

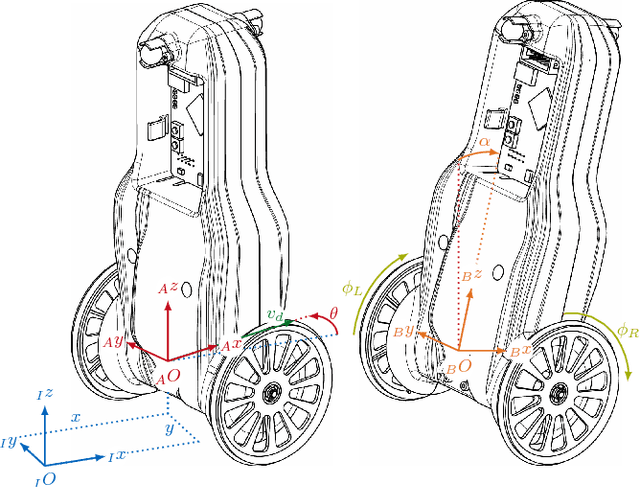
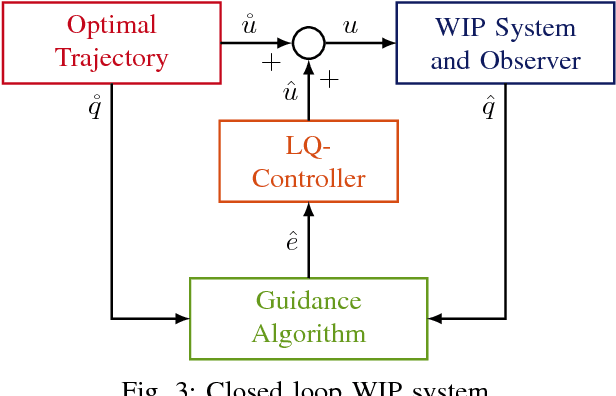
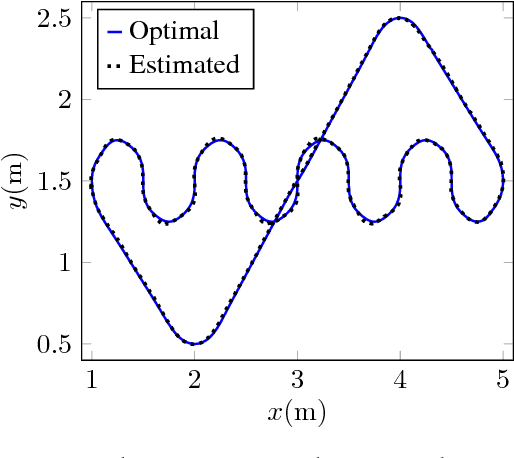
The Wheeled Inverted Pendulum (WIP) is an underactuated, nonholonomic mechanical system, and has been popularized commercially as the Segway. Designing a control law for motion planning, that incorporates the state and control constraints, while respecting the configuration manifold, is a challenging problem. In this article we derive a discrete-time model of the WIP system using discrete mechanics and generate optimal trajectories for the WIP system by solving a discrete-time constrained optimal control problem, and describe a nonlinear continuous-time model with parameters for designing close loop LQ-controller. A dual control architecture is implemented in which the designed optimal trajectory is then provided as a reference to the robot with the optimal control trajectory as a feedforward control action, and an LQ-controller is employed to mitigate noise and disturbances for ensuing stable motion of the WIP system. While performing experiments on the WIP system involving aggressive maneuvers with fairly sharp turns, we found a high degree of congruence in the designed optimal trajectories and the path traced by the robot while tracking these trajectories; this corroborates the validity of the nonlinear model and the control scheme. Finally, these experiments demonstrate the highly nonlinear nature of the WIP system and robustness of the control scheme.

A complete characterization of optimal dictionaries for least squares representation

Dictionaries are collections of vectors used for representations of elements in Euclidean spaces. While recent research on optimal dictionaries is focussed on providing sparse (i.e., $\ell_0$-optimal,) representations, here we consider the problem of finding optimal dictionaries such that representations of samples of a random vector are optimal in an $\ell_2$-sense. For us, optimality of representation is equivalent to minimization of the average $\ell_2$-norm of the coefficients used to represent the random vector, with the lengths of the dictionary vectors being specified a priori. With the help of recent results on rank-$1$ decompositions of symmetric positive semidefinite matrices and the theory of majorization, we provide a complete characterization of $\ell_2$-optimal dictionaries. Our results are accompanied by polynomial time algorithms that construct $\ell_2$-optimal dictionaries from given data.

Optimal dictionary for least squares representation

Dictionaries are collections of vectors used for representations of random vectors in Euclidean spaces. Recent research on optimal dictionaries is focused on constructing dictionaries that offer sparse representations, i.e., $\ell_0$-optimal representations. Here we consider the problem of finding optimal dictionaries with which representations of samples of a random vector are optimal in an $\ell_2$-sense: optimality of representation is defined as attaining the minimal average $\ell_2$-norm of the coefficients used to represent the random vector. With the help of recent results on rank-$1$ decompositions of symmetric positive semidefinite matrices, we provide an explicit description of $\ell_2$-optimal dictionaries as well as their algorithmic constructions in polynomial time.