Felix Anhalt
Structure-preserving constrained optimal trajectory planning of a wheeled inverted pendulum
Nov 29, 2018
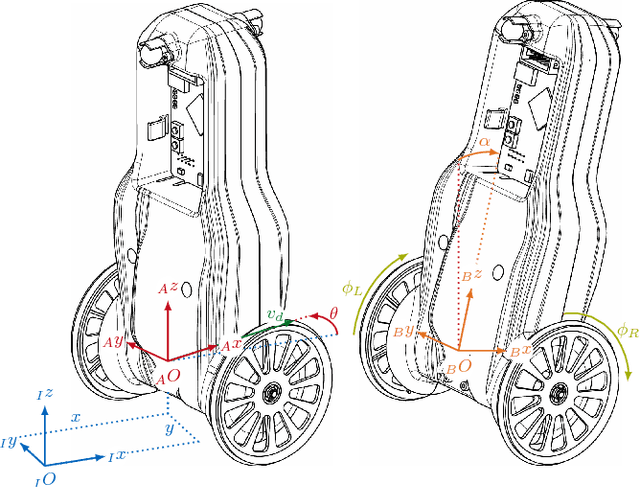
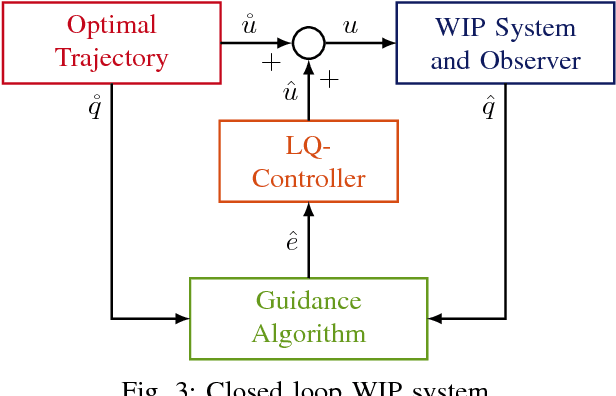
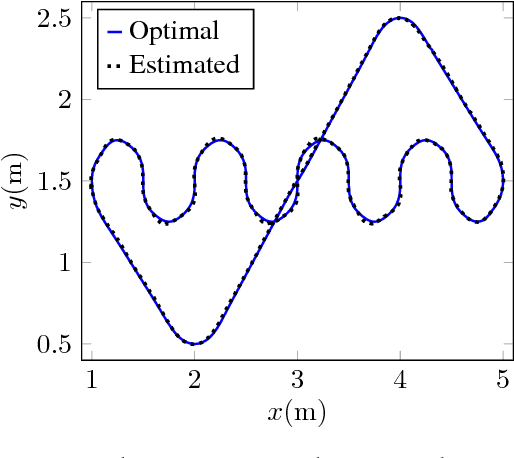
Abstract:The Wheeled Inverted Pendulum (WIP) is an underactuated, nonholonomic mechanical system, and has been popularized commercially as the Segway. Designing a control law for motion planning, that incorporates the state and control constraints, while respecting the configuration manifold, is a challenging problem. In this article we derive a discrete-time model of the WIP system using discrete mechanics and generate optimal trajectories for the WIP system by solving a discrete-time constrained optimal control problem, and describe a nonlinear continuous-time model with parameters for designing close loop LQ-controller. A dual control architecture is implemented in which the designed optimal trajectory is then provided as a reference to the robot with the optimal control trajectory as a feedforward control action, and an LQ-controller is employed to mitigate noise and disturbances for ensuing stable motion of the WIP system. While performing experiments on the WIP system involving aggressive maneuvers with fairly sharp turns, we found a high degree of congruence in the designed optimal trajectories and the path traced by the robot while tracking these trajectories; this corroborates the validity of the nonlinear model and the control scheme. Finally, these experiments demonstrate the highly nonlinear nature of the WIP system and robustness of the control scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge