Boris Lohmann
Longitudinal Control for Autonomous Racing with Combustion Engine Vehicles
Apr 24, 2025
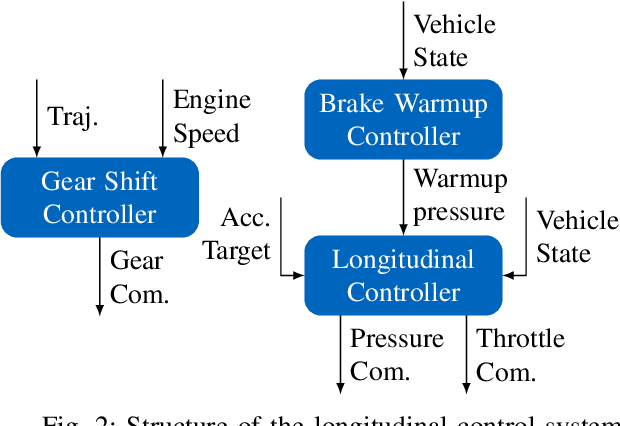
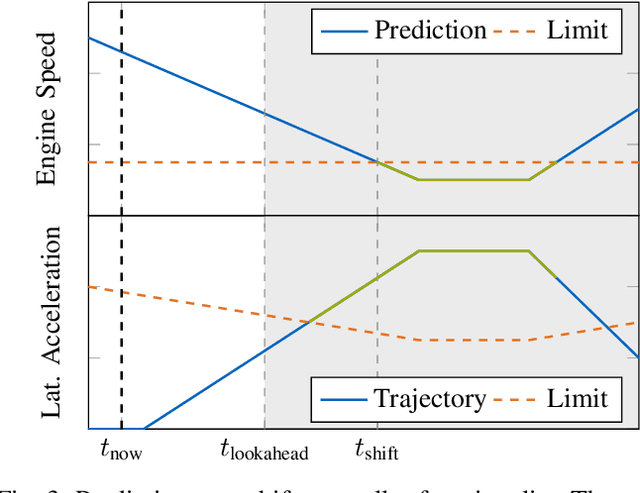
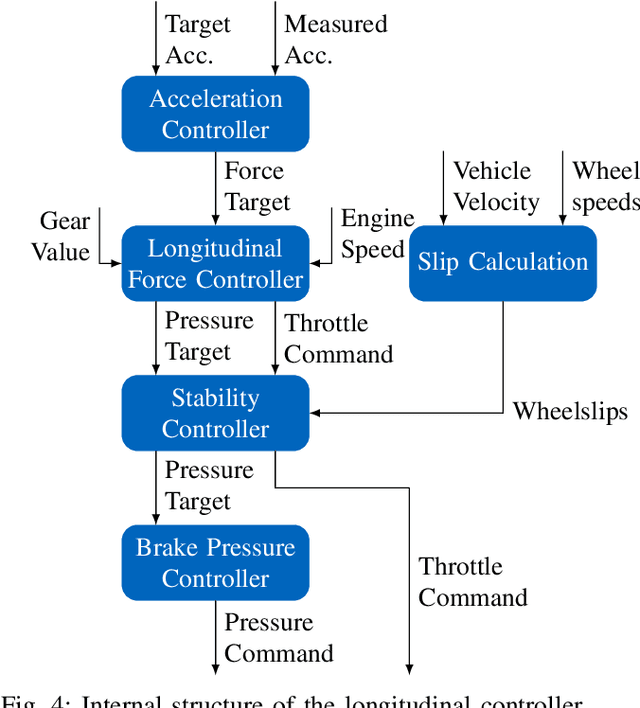
Abstract:Usually, a controller for path- or trajectory tracking is employed in autonomous driving. Typically, these controllers generate high-level commands like longitudinal acceleration or force. However, vehicles with combustion engines expect different actuation inputs. This paper proposes a longitudinal control concept that translates high-level trajectory-tracking commands to the required low-level vehicle commands such as throttle, brake pressure and a desired gear. We chose a modular structure to easily integrate different trajectory-tracking control algorithms and vehicles. The proposed control concept enables a close tracking of the high-level control command. An anti-lock braking system, traction control, and brake warmup control also ensure a safe operation during real-world tests. We provide experimental validation of our concept using real world data with longitudinal accelerations reaching up to $25 \, \frac{\mathrm{m}}{\mathrm{s}^2}$. The experiments were conducted using the EAV24 racecar during the first event of the Abu Dhabi Autonomous Racing League on the Yas Marina Formula 1 Circuit.
Trajectory Planning using Reinforcement Learning for Interactive Overtaking Maneuvers in Autonomous Racing Scenarios
Apr 16, 2024



Abstract:Conventional trajectory planning approaches for autonomous racing are based on the sequential execution of prediction of the opposing vehicles and subsequent trajectory planning for the ego vehicle. If the opposing vehicles do not react to the ego vehicle, they can be predicted accurately. However, if there is interaction between the vehicles, the prediction loses its validity. For high interaction, instead of a planning approach that reacts exclusively to the fixed prediction, a trajectory planning approach is required that incorporates the interaction with the opposing vehicles. This paper demonstrates the limitations of a widely used conventional sampling-based approach within a highly interactive blocking scenario. We show that high success rates are achieved for less aggressive blocking behavior but that the collision rate increases with more significant interaction. We further propose a novel Reinforcement Learning (RL)-based trajectory planning approach for racing that explicitly exploits the interaction with the opposing vehicle without requiring a prediction. In contrast to the conventional approach, the RL-based approach achieves high success rates even for aggressive blocking behavior. Furthermore, we propose a novel safety layer (SL) that intervenes when the trajectory generated by the RL-based approach is infeasible. In that event, the SL generates a sub-optimal but feasible trajectory, avoiding termination of the scenario due to a not found valid solution.
Sampling-Based Motion Planning with Online Racing Line Generation for Autonomous Driving on Three-Dimensional Race Tracks
Mar 27, 2024Abstract:Existing approaches to trajectory planning for autonomous racing employ sampling-based methods, generating numerous jerk-optimal trajectories and selecting the most favorable feasible trajectory based on a cost function penalizing deviations from an offline-calculated racing line. While successful on oval tracks, these methods face limitations on complex circuits due to the simplistic geometry of jerk-optimal edges failing to capture the complexity of the racing line. Additionally, they only consider two-dimensional tracks, potentially neglecting or surpassing the actual dynamic potential. In this paper, we present a sampling-based local trajectory planning approach for autonomous racing that can maintain the lap time of the racing line even on complex race tracks and consider the race track's three-dimensional effects. In simulative experiments, we demonstrate that our approach achieves lower lap times and improved utilization of dynamic limits compared to existing approaches. We also investigate the impact of online racing line generation, in which the time-optimal solution is planned from the current vehicle state for a limited spatial horizon, in contrast to a closed racing line calculated offline. We show that combining the sampling-based planner with the online racing line generation can significantly reduce lap times in multi-vehicle scenarios.
Open-Loop and Feedback Nash Trajectories for Competitive Racing with iLQGames
Feb 02, 2024Abstract:Interaction-aware trajectory planning is crucial for closing the gap between autonomous racing cars and human racing drivers. Prior work has applied game theory as it provides equilibrium concepts for non-cooperative dynamic problems. With this contribution, we formulate racing as a dynamic game and employ a variant of iLQR, called iLQGames, to solve the game. iLQGames finds trajectories for all players that satisfy the equilibrium conditions for a linear-quadratic approximation of the game and has been previously applied in traffic scenarios. We analyze the algorithm's applicability for trajectory planning in racing scenarios and evaluate it based on interaction awareness, competitiveness, and safety. With the ability of iLQGames to solve for open-loop and feedback Nash equilibria, we compare the behavioral outcomes of the two equilibrium concepts in simple scenarios on a straight track section.
Hierarchical Time-Optimal Planning for Multi-Vehicle Racing
Sep 13, 2023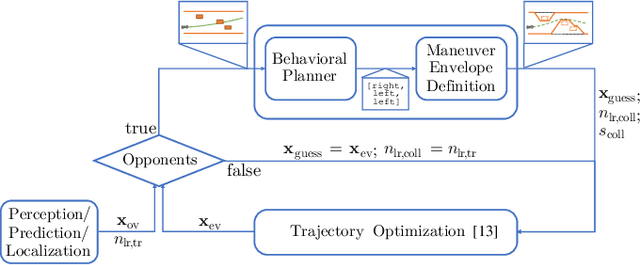
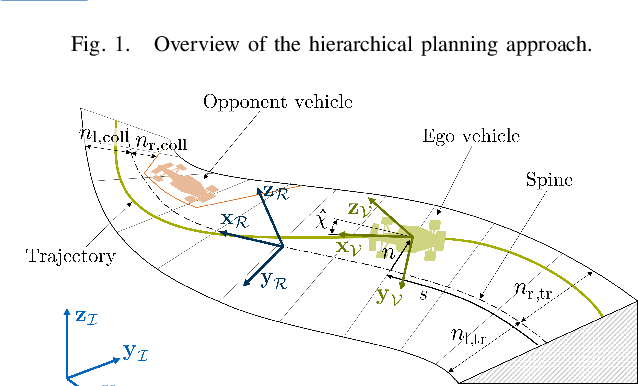
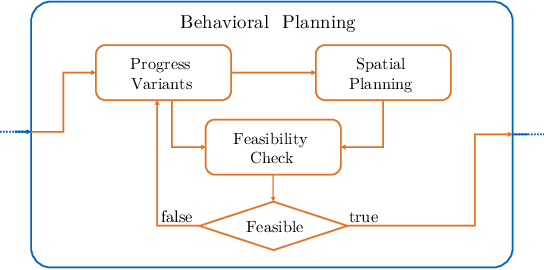
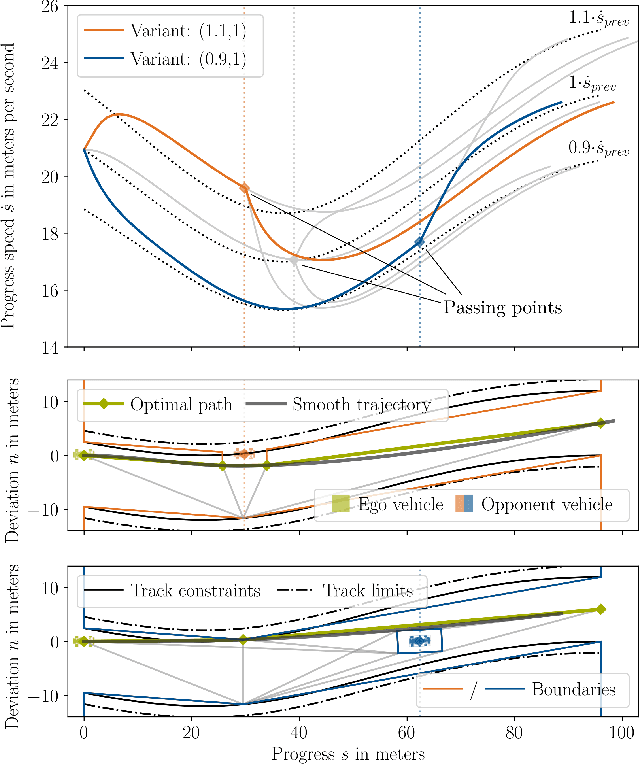
Abstract:This paper presents a hierarchical planning algorithm for racing with multiple opponents. The two-stage approach consists of a high-level behavioral planning step and a low-level optimization step. By combining discrete and continuous planning methods, our algorithm encourages global time optimality without being limited by coarse discretization. In the behavioral planning step, the fastest behavior is determined with a low-resolution spatio-temporal visibility graph. Based on the selected behavior, we calculate maneuver envelopes that are subsequently applied as constraints in a time-optimal control problem. The performance of our method is comparable to a parallel approach that selects the fastest trajectory from multiple optimizations with different behavior classes. However, our algorithm can be executed on a single core. This significantly reduces computational requirements, especially when multiple opponents are involved. Therefore, the proposed method is an efficient and practical solution for real-time multi-vehicle racing scenarios.
Online Time-Optimal Trajectory Planning on Three-Dimensional Race Tracks
Apr 21, 2023
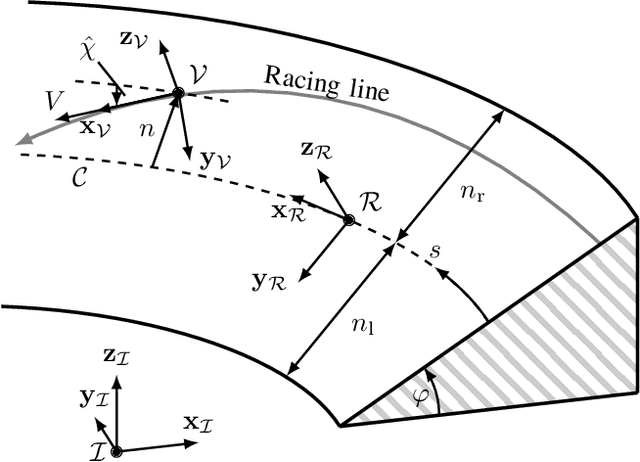
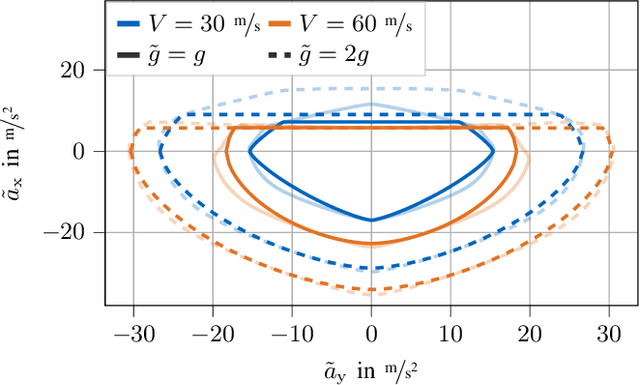
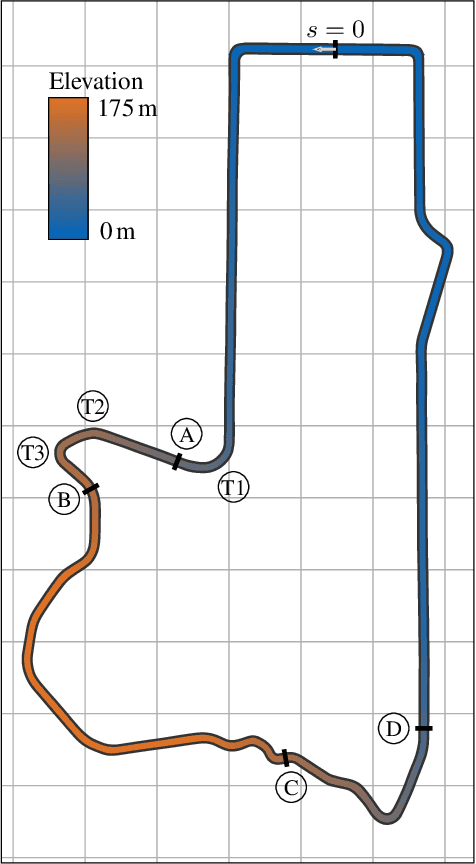
Abstract:We propose an online planning approach for racing that generates the time-optimal trajectory for the upcoming track section. The resulting trajectory takes the current vehicle state, effects caused by \acl{3D} track geometries, and speed limits dictated by the race rules into account. In each planning step, an optimal control problem is solved, making a quasi-steady-state assumption with a point mass model constrained by gg-diagrams. For its online applicability, we propose an efficient representation of the gg-diagrams and identify negligible terms to reduce the computational effort. We demonstrate that the online planning approach can reproduce the lap times of an offline-generated racing line during single vehicle racing. Moreover, it finds a new time-optimal solution when a deviation from the original racing line is necessary, e.g., during an overtaking maneuver. Motivated by the application in a rule-based race, we also consider the scenario of a speed limit lower than the current vehicle velocity. We introduce an initializable slack variable to generate feasible trajectories despite the constraint violation while reducing the velocity to comply with the rules.
TUM Autonomous Motorsport: An Autonomous Racing Software for the Indy Autonomous Challenge
May 31, 2022
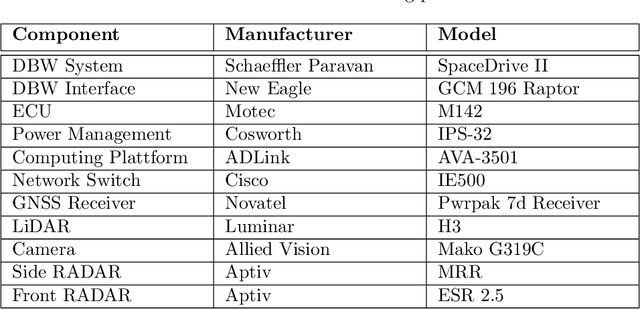
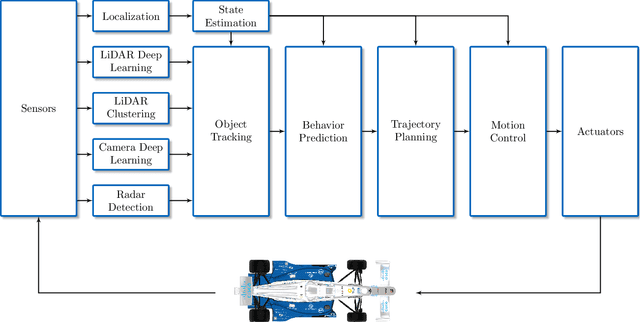
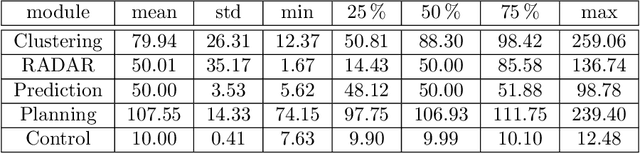
Abstract:For decades, motorsport has been an incubator for innovations in the automotive sector and brought forth systems like disk brakes or rearview mirrors. Autonomous racing series such as Roborace, F1Tenth, or the Indy Autonomous Challenge (IAC) are envisioned as playing a similar role within the autonomous vehicle sector, serving as a proving ground for new technology at the limits of the autonomous systems capabilities. This paper outlines the software stack and approach of the TUM Autonomous Motorsport team for their participation in the Indy Autonomous Challenge, which holds two competitions: A single-vehicle competition on the Indianapolis Motor Speedway and a passing competition at the Las Vegas Motor Speedway. Nine university teams used an identical vehicle platform: A modified Indy Lights chassis equipped with sensors, a computing platform, and actuators. All the teams developed different algorithms for object detection, localization, planning, prediction, and control of the race cars. The team from TUM placed first in Indianapolis and secured second place in Las Vegas. During the final of the passing competition, the TUM team reached speeds and accelerations close to the limit of the vehicle, peaking at around 270 km/h and 28 ms2. This paper will present details of the vehicle hardware platform, the developed algorithms, and the workflow to test and enhance the software applied during the two-year project. We derive deep insights into the autonomous vehicle's behavior at high speed and high acceleration by providing a detailed competition analysis. Based on this, we deduce a list of lessons learned and provide insights on promising areas of future work based on the real-world evaluation of the displayed concepts.
Indy Autonomous Challenge -- Autonomous Race Cars at the Handling Limits
Feb 08, 2022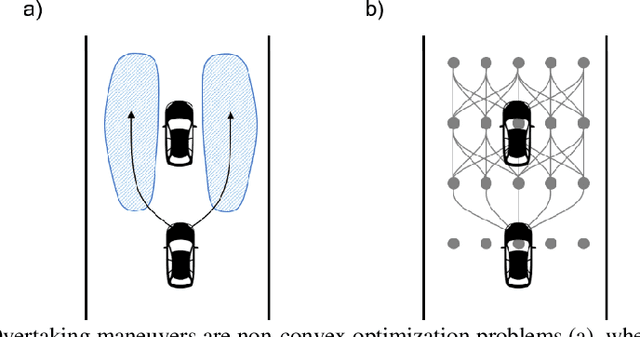
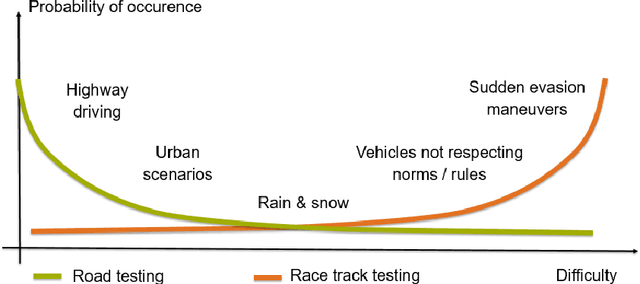

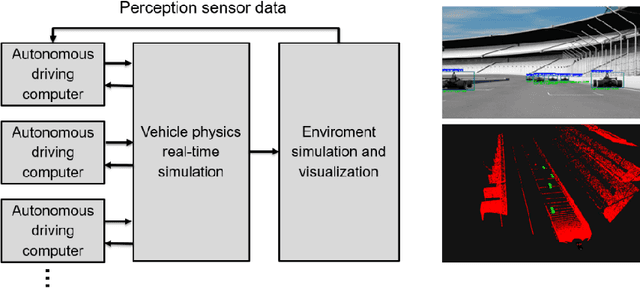
Abstract:Motorsport has always been an enabler for technological advancement, and the same applies to the autonomous driving industry. The team TUM Auton-omous Motorsports will participate in the Indy Autonomous Challenge in Octo-ber 2021 to benchmark its self-driving software-stack by racing one out of ten autonomous Dallara AV-21 racecars at the Indianapolis Motor Speedway. The first part of this paper explains the reasons for entering an autonomous vehicle race from an academic perspective: It allows focusing on several edge cases en-countered by autonomous vehicles, such as challenging evasion maneuvers and unstructured scenarios. At the same time, it is inherently safe due to the motor-sport related track safety precautions. It is therefore an ideal testing ground for the development of autonomous driving algorithms capable of mastering the most challenging and rare situations. In addition, we provide insight into our soft-ware development workflow and present our Hardware-in-the-Loop simulation setup. It is capable of running simulations of up to eight autonomous vehicles in real time. The second part of the paper gives a high-level overview of the soft-ware architecture and covers our development priorities in building a high-per-formance autonomous racing software: maximum sensor detection range, relia-ble handling of multi-vehicle situations, as well as reliable motion control under uncertainty.
Structure-preserving constrained optimal trajectory planning of a wheeled inverted pendulum
Nov 29, 2018
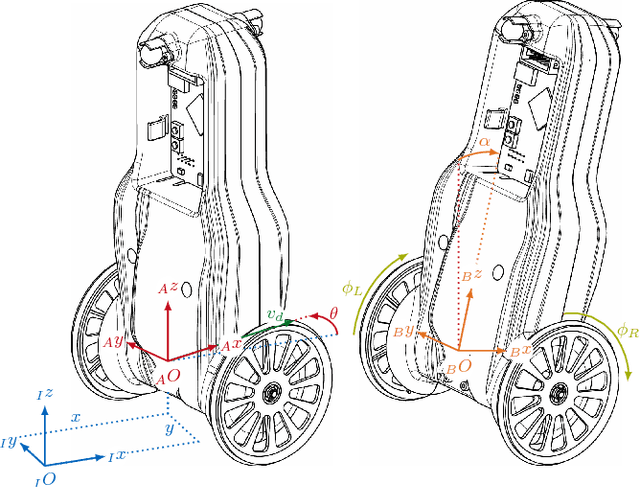
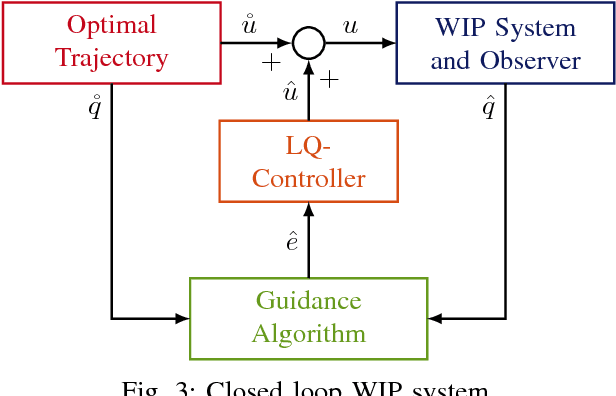
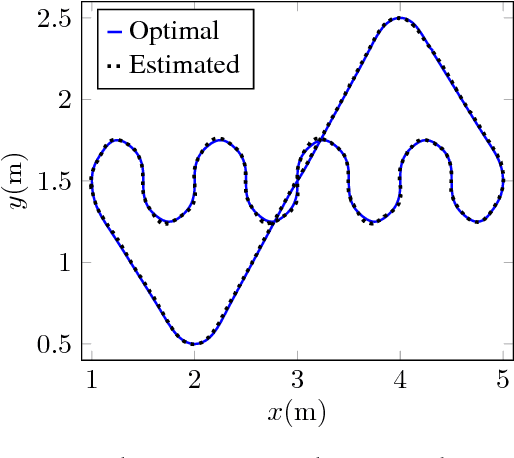
Abstract:The Wheeled Inverted Pendulum (WIP) is an underactuated, nonholonomic mechanical system, and has been popularized commercially as the Segway. Designing a control law for motion planning, that incorporates the state and control constraints, while respecting the configuration manifold, is a challenging problem. In this article we derive a discrete-time model of the WIP system using discrete mechanics and generate optimal trajectories for the WIP system by solving a discrete-time constrained optimal control problem, and describe a nonlinear continuous-time model with parameters for designing close loop LQ-controller. A dual control architecture is implemented in which the designed optimal trajectory is then provided as a reference to the robot with the optimal control trajectory as a feedforward control action, and an LQ-controller is employed to mitigate noise and disturbances for ensuing stable motion of the WIP system. While performing experiments on the WIP system involving aggressive maneuvers with fairly sharp turns, we found a high degree of congruence in the designed optimal trajectories and the path traced by the robot while tracking these trajectories; this corroborates the validity of the nonlinear model and the control scheme. Finally, these experiments demonstrate the highly nonlinear nature of the WIP system and robustness of the control scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge