Scenario approach for minmax optimization with emphasis on the nonconvex case: positive results and caveats

We treat the so-called scenario approach, a popular probabilistic approximation method for robust minmax optimization problems via independent and indentically distributed (i.i.d) sampling from the uncertainty set, from various perspectives. The scenario approach is well-studied in the important case of convex robust optimization problems, and here we examine how the phenomenon of concentration of measures affects the i.i.d sampling aspect of the scenario approach in high dimensions and its relation with the optimal values. Moreover, we perform a detailed study of both the asymptotic behaviour (consistency) and finite time behaviour of the scenario approach in the more general setting of nonconvex minmax optimization problems. In the direction of the asymptotic behaviour of the scenario approach, we present an obstruction to consistency that arises when the decision set is noncompact. In the direction of finite sample guarantees, we establish a general methodology for extracting `probably approximately correct' type estimates for the finite sample behaviour of the scenario approach for a large class of nonconvex problems.

A Lagrangian Model to Predict Microscallop Motion in non Newtonian Fluids

The need to develop models to predict the motion of microrobots, or robots of a much smaller scale, moving in fluids in a low Reynolds number regime, and in particular, in non Newtonian fluids, cannot be understated. The article develops a Lagrangian based model for one such mechanism - a two-link mechanism termed a microscallop, moving in a low Reynolds number environment in a non Newtonian fluid. The modelling proceeds through the conventional Lagrangian construction for a two-link mechanism and then goes on to model the external fluid forces using empirically based models for viscosity to complete the dynamic model. The derived model is then simulated for different initial conditions and key parameters of the non Newtonian fluid, and the results are corroborated with a few existing experimental results on a similar mechanism under identical conditions. Lastly, with a view to implementing control algorithms we explore accessibility of the system at certain configurations.

Locomotion of the generalized Purcell's swimmer : Modelling, controllability and motion primitives

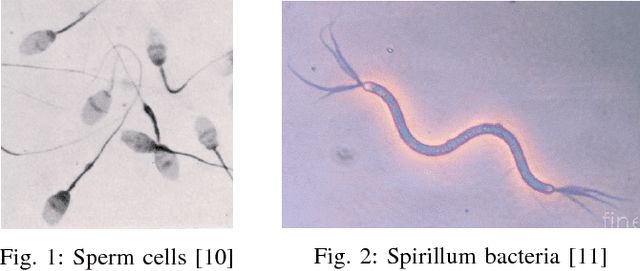
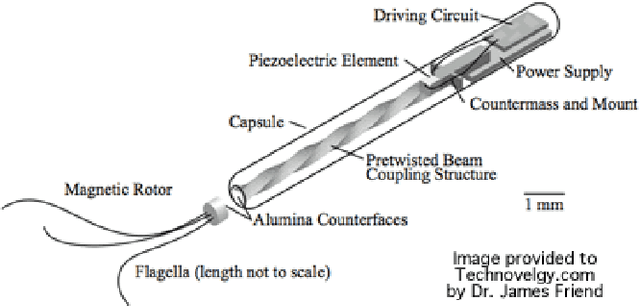
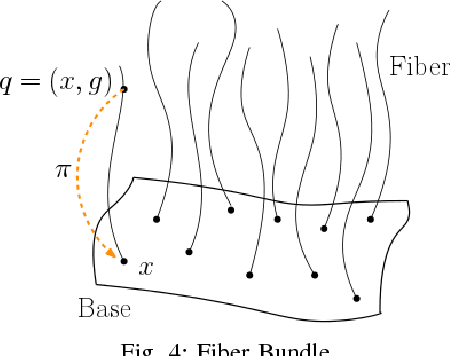
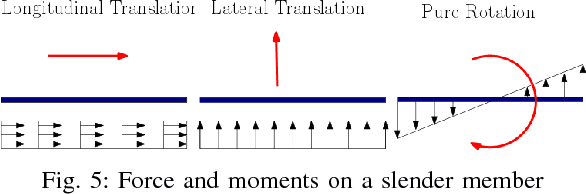
Micro-robotics at low Reynolds number has been a growing area of research over the past decade. We propose and study a generalized 3-link robotic swimmer inspired by the planar Purcell's swimmer. By incorporating out-of-plane motion of the outer limbs, this mechanism generalizes the planar Purcell's swimmer, which has been widely studied in the literature. Such an evolution of the limbs' motion results in the swimmer's base link evolving in a 3-dimensional space. The swimmer's configuration space admits a trivial principal fiber bundle structure, which along with the slender body theory at the low Reynolds number regime, facilitates in obtaining a principal kinematic form of the equations. We derive a coordinate-free expression for the local form of the kinematic connection. A novel approach for local controllability analysis of this 3-dimensional swimmer in the low Reynolds number regime is presented by employing the controllability results of the planar Purcell's swimmer. This is followed by control synthesis using the motion primitives approach. We prove the existence of motion primitives based control sequence for maneuvering the swimmer's base link whose motion evolves on a Lie group. Using the principal fiber bundle structure, an algorithm for point to point reconfiguration of the swimmer is presented. A set of control sequences for translational and rotational maneuvers is then provided along with numerical simulations.

Notes on geometry of locomotion of 3-dimensional version of the Purcell's swimmer

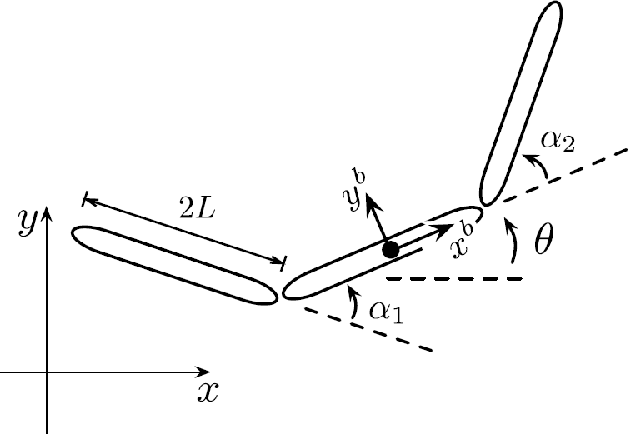
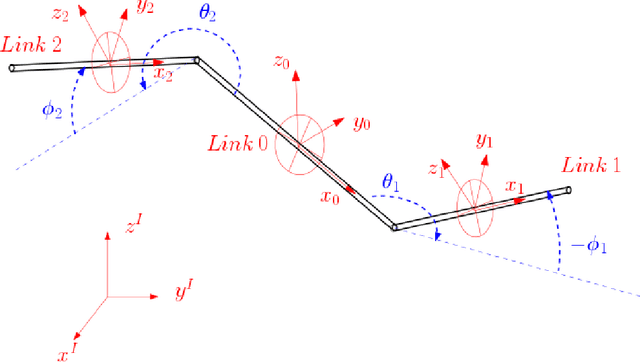
We present a generalized, 3 dimensional version of the Purcell's swimmer which is a planar mechanism locomoting at low Reynlods number regime. We use Cox theory and resistive force theory to come up with the forces acting on the system. We finally come up with a purely kinematic form of the system's equations.