Locomotion of the generalized Purcell's swimmer : Modelling, controllability and motion primitives

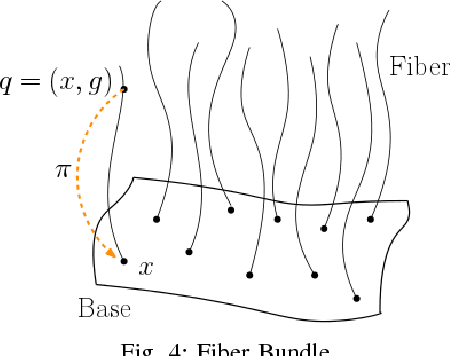
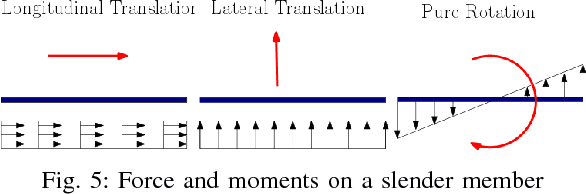
Micro-robotics at low Reynolds number has been a growing area of research over the past decade. We propose and study a generalized 3-link robotic swimmer inspired by the planar Purcell's swimmer. By incorporating out-of-plane motion of the outer limbs, this mechanism generalizes the planar Purcell's swimmer, which has been widely studied in the literature. Such an evolution of the limbs' motion results in the swimmer's base link evolving in a 3-dimensional space. The swimmer's configuration space admits a trivial principal fiber bundle structure, which along with the slender body theory at the low Reynolds number regime, facilitates in obtaining a principal kinematic form of the equations. We derive a coordinate-free expression for the local form of the kinematic connection. A novel approach for local controllability analysis of this 3-dimensional swimmer in the low Reynolds number regime is presented by employing the controllability results of the planar Purcell's swimmer. This is followed by control synthesis using the motion primitives approach. We prove the existence of motion primitives based control sequence for maneuvering the swimmer's base link whose motion evolves on a Lie group. Using the principal fiber bundle structure, an algorithm for point to point reconfiguration of the swimmer is presented. A set of control sequences for translational and rotational maneuvers is then provided along with numerical simulations.

Notes on geometry of locomotion of 3-dimensional version of the Purcell's swimmer

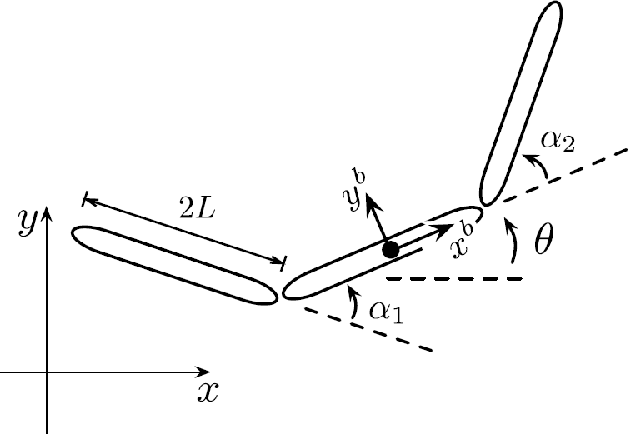
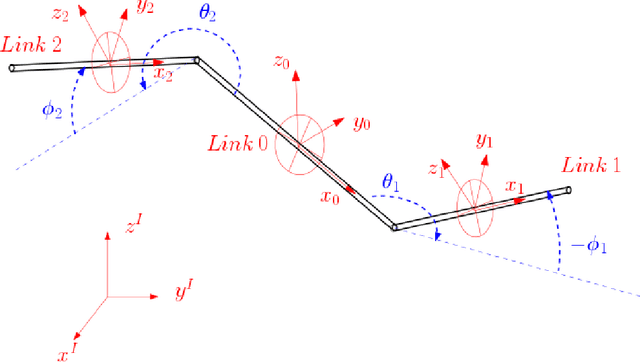
We present a generalized, 3 dimensional version of the Purcell's swimmer which is a planar mechanism locomoting at low Reynlods number regime. We use Cox theory and resistive force theory to come up with the forces acting on the system. We finally come up with a purely kinematic form of the system's equations.