Ashwin Aravind
A Moreau Envelope Approach for LQR Meta-Policy Estimation
Mar 26, 2024

Abstract:We study the problem of policy estimation for the Linear Quadratic Regulator (LQR) in discrete-time linear time-invariant uncertain dynamical systems. We propose a Moreau Envelope-based surrogate LQR cost, built from a finite set of realizations of the uncertain system, to define a meta-policy efficiently adjustable to new realizations. Moreover, we design an algorithm to find an approximate first-order stationary point of the meta-LQR cost function. Numerical results show that the proposed approach outperforms naive averaging of controllers on new realizations of the linear system. We also provide empirical evidence that our method has better sample complexity than Model-Agnostic Meta-Learning (MAML) approaches.
Cross apprenticeship learning framework: Properties and solution approaches
Sep 06, 2022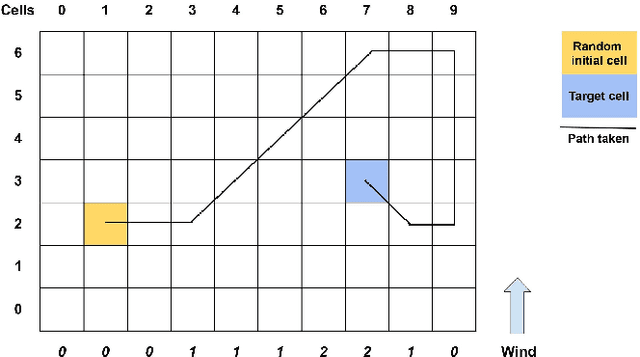
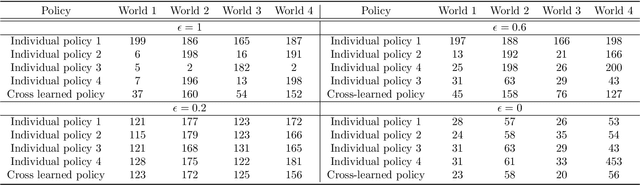
Abstract:Apprenticeship learning is a framework in which an agent learns a policy to perform a given task in an environment using example trajectories provided by an expert. In the real world, one might have access to expert trajectories in different environments where the system dynamics is different while the learning task is the same. For such scenarios, two types of learning objectives can be defined. One where the learned policy performs very well in one specific environment and another when it performs well across all environments. To balance these two objectives in a principled way, our work presents the cross apprenticeship learning (CAL) framework. This consists of an optimization problem where an optimal policy for each environment is sought while ensuring that all policies remain close to each other. This nearness is facilitated by one tuning parameter in the optimization problem. We derive properties of the optimizers of the problem as the tuning parameter varies. Since the problem is nonconvex, we provide a convex outer approximation. Finally, we demonstrate the attributes of our framework in the context of a navigation task in a windy gridworld environment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge