A Moreau Envelope Approach for LQR Meta-Policy Estimation

We study the problem of policy estimation for the Linear Quadratic Regulator (LQR) in discrete-time linear time-invariant uncertain dynamical systems. We propose a Moreau Envelope-based surrogate LQR cost, built from a finite set of realizations of the uncertain system, to define a meta-policy efficiently adjustable to new realizations. Moreover, we design an algorithm to find an approximate first-order stationary point of the meta-LQR cost function. Numerical results show that the proposed approach outperforms naive averaging of controllers on new realizations of the linear system. We also provide empirical evidence that our method has better sample complexity than Model-Agnostic Meta-Learning (MAML) approaches.

Improving Denoising Diffusion Probabilistic Models via Exploiting Shared Representations

In this work, we address the challenge of multi-task image generation with limited data for denoising diffusion probabilistic models (DDPM), a class of generative models that produce high-quality images by reversing a noisy diffusion process. We propose a novel method, SR-DDPM, that leverages representation-based techniques from few-shot learning to effectively learn from fewer samples across different tasks. Our method consists of a core meta architecture with shared parameters, i.e., task-specific layers with exclusive parameters. By exploiting the similarity between diverse data distributions, our method can scale to multiple tasks without compromising the image quality. We evaluate our method on standard image datasets and show that it outperforms both unconditional and conditional DDPM in terms of FID and SSIM metrics.

Adaptive Federated Learning with Auto-Tuned Clients

Federated learning (FL) is a distributed machine learning framework where the global model of a central server is trained via multiple collaborative steps by participating clients without sharing their data. While being a flexible framework, where the distribution of local data, participation rate, and computing power of each client can greatly vary, such flexibility gives rise to many new challenges, especially in the hyperparameter tuning on both the server and the client side. We propose $\Delta$-SGD, a simple step size rule for SGD that enables each client to use its own step size by adapting to the local smoothness of the function each client is optimizing. We provide theoretical and empirical results where the benefit of the client adaptivity is shown in various FL scenarios. In particular, our proposed method achieves TOP-1 accuracy in 73% and TOP-2 accuracy in 100% of the experiments considered without additional tuning.

On First-Order Meta-Reinforcement Learning with Moreau Envelopes

Meta-Reinforcement Learning (MRL) is a promising framework for training agents that can quickly adapt to new environments and tasks. In this work, we study the MRL problem under the policy gradient formulation, where we propose a novel algorithm that uses Moreau envelope surrogate regularizers to jointly learn a meta-policy that is adjustable to the environment of each individual task. Our algorithm, called Moreau Envelope Meta-Reinforcement Learning (MEMRL), learns a meta-policy that can adapt to a distribution of tasks by efficiently updating the policy parameters using a combination of gradient-based optimization and Moreau Envelope regularization. Moreau Envelopes provide a smooth approximation of the policy optimization problem, which enables us to apply standard optimization techniques and converge to an appropriate stationary point. We provide a detailed analysis of the MEMRL algorithm, where we show a sublinear convergence rate to a first-order stationary point for non-convex policy gradient optimization. We finally show the effectiveness of MEMRL on a multi-task 2D-navigation problem.

PersA-FL: Personalized Asynchronous Federated Learning

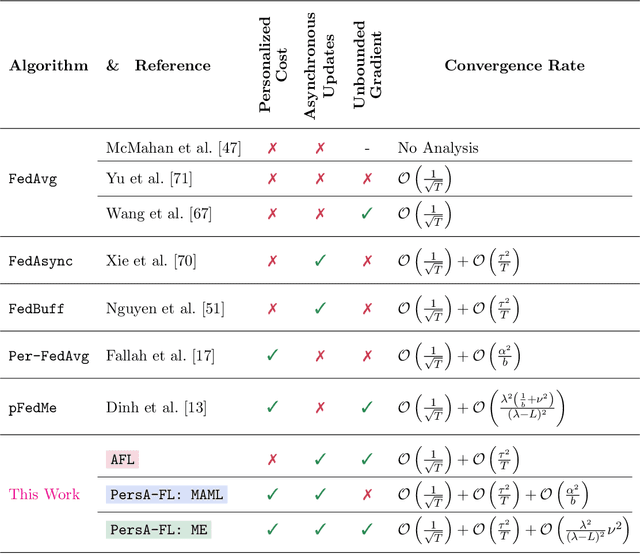
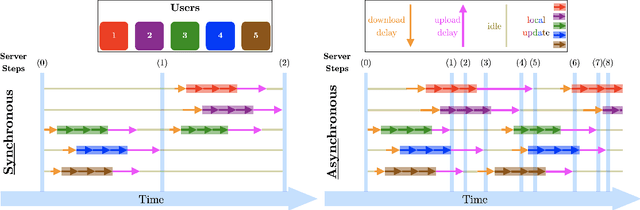
We study the personalized federated learning problem under asynchronous updates. In this problem, each client seeks to obtain a personalized model that simultaneously outperforms local and global models. We consider two optimization-based frameworks for personalization: (i) Model-Agnostic Meta-Learning (MAML) and (ii) Moreau Envelope (ME). MAML involves learning a joint model adapted for each client through fine-tuning, whereas ME requires a bi-level optimization problem with implicit gradients to enforce personalization via regularized losses. We focus on improving the scalability of personalized federated learning by removing the synchronous communication assumption. Moreover, we extend the studied function class by removing boundedness assumptions on the gradient norm. Our main technical contribution is a unified proof for asynchronous federated learning with bounded staleness that we apply to MAML and ME personalization frameworks. For the smooth and non-convex functions class, we show the convergence of our method to a first-order stationary point. We illustrate the performance of our method and its tolerance to staleness through experiments for classification tasks over heterogeneous datasets.

Unbounded Gradients in Federated Leaning with Buffered Asynchronous Aggregation

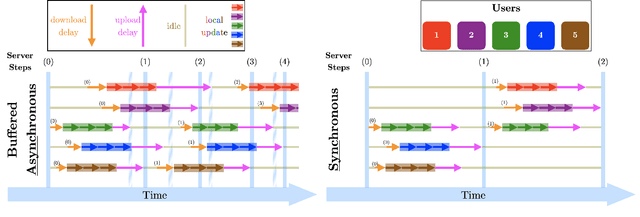
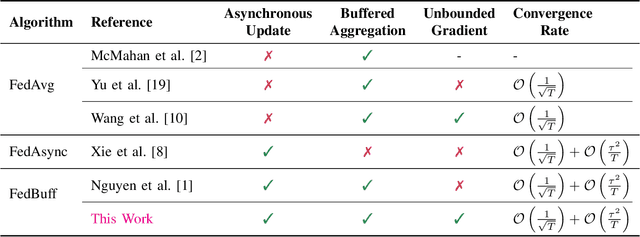
Synchronous updates may compromise the efficiency of cross-device federated learning once the number of active clients increases. The \textit{FedBuff} algorithm (Nguyen et al., 2022) alleviates this problem by allowing asynchronous updates (staleness), which enhances the scalability of training while preserving privacy via secure aggregation. We revisit the \textit{FedBuff} algorithm for asynchronous federated learning and extend the existing analysis by removing the boundedness assumptions from the gradient norm. This paper presents a theoretical analysis of the convergence rate of this algorithm when heterogeneity in data, batch size, and delay are considered.

On Arbitrary Compression for Decentralized Consensus and Stochastic Optimization over Directed Networks

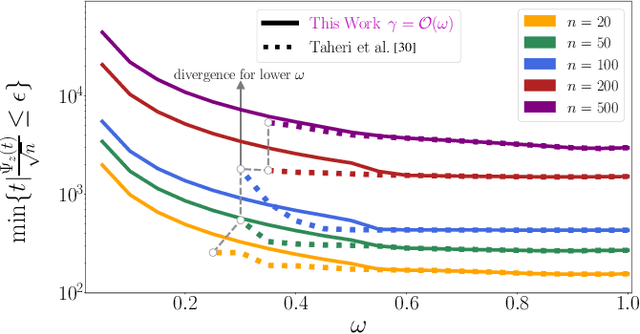
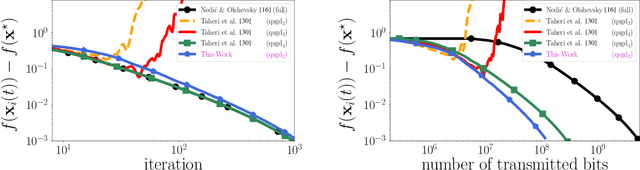
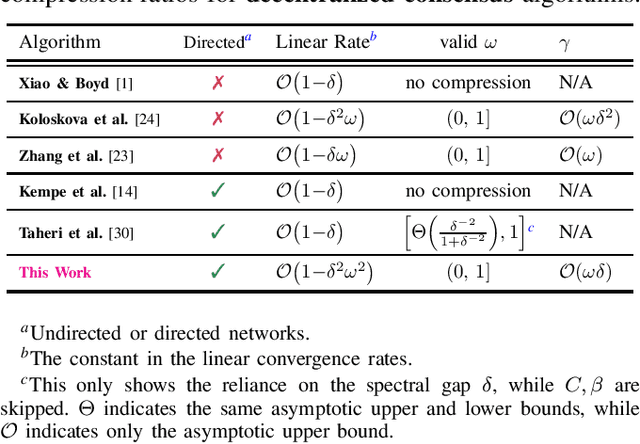
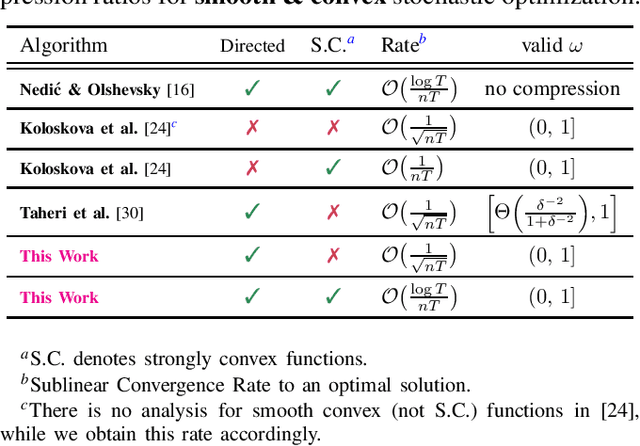
We study the decentralized consensus and stochastic optimization problems with compressed communications over static directed graphs. We propose an iterative gradient-based algorithm that compresses messages according to a desired compression ratio. The proposed method provably reduces the communication overhead on the network at every communication round. Contrary to existing literature, we allow for arbitrary compression ratios in the communicated messages. We show a linear convergence rate for the proposed method on the consensus problem. Moreover, we provide explicit convergence rates for decentralized stochastic optimization problems on smooth functions that are either (i) strongly convex, (ii) convex, or (iii) non-convex. Finally, we provide numerical experiments to illustrate convergence under arbitrary compression ratios and the communication efficiency of our algorithm.

Local Stochastic Factored Gradient Descent for Distributed Quantum State Tomography

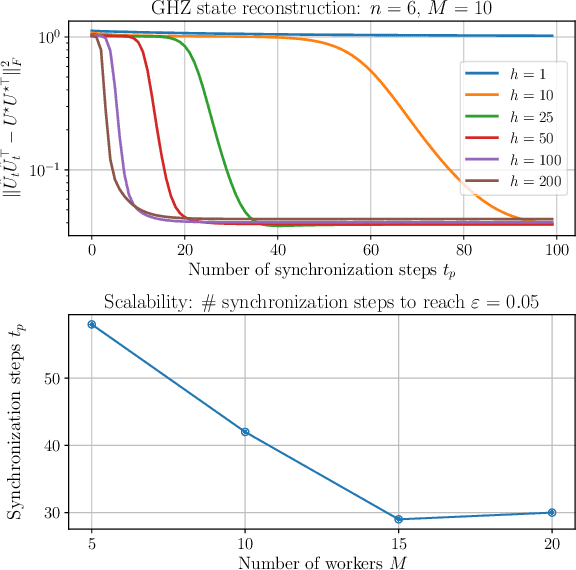
We propose a distributed Quantum State Tomography (QST) protocol, named Local Stochastic Factored Gradient Descent (Local SFGD), to learn the low-rank factor of a density matrix over a set of local machines. QST is the canonical procedure to characterize the state of a quantum system, which we formulate as a stochastic nonconvex smooth optimization problem. Physically, the estimation of a low-rank density matrix helps characterizing the amount of noise introduced by quantum computation. Theoretically, we prove the local convergence of Local SFGD for a general class of restricted strongly convex/smooth loss functions, i.e., Local SFGD converges locally to a small neighborhood of the global optimum at a linear rate with a constant step size, while it locally converges exactly at a sub-linear rate with diminishing step sizes. With a proper initialization, local convergence results imply global convergence. We validate our theoretical findings with numerical simulations of QST on the Greenberger-Horne-Zeilinger (GHZ) state.

Scalable Average Consensus with Compressed Communications

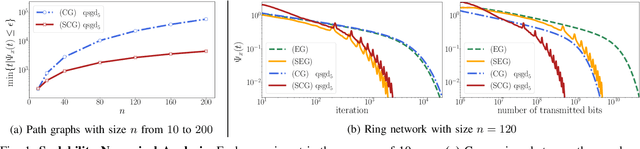
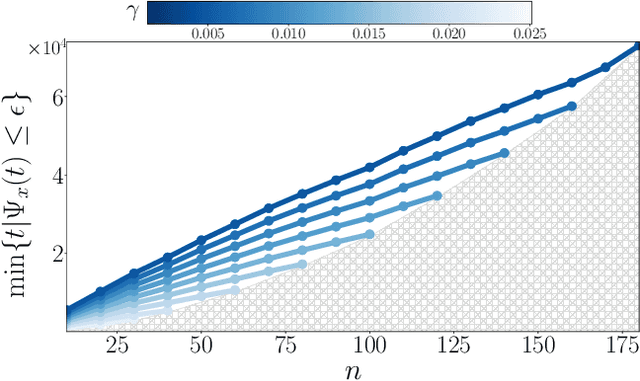
We propose a new decentralized average consensus algorithm with compressed communication that scales linearly with the network size n. We prove that the proposed method converges to the average of the initial values held locally by the agents of a network when agents are allowed to communicate with compressed messages. The proposed algorithm works for a broad class of compression operators (possibly biased), where agents interact over arbitrary static, undirected, and connected networks. We further present numerical experiments that confirm our theoretical results and illustrate the scalability and communication efficiency of our algorithm.

Momentum-inspired Low-Rank Coordinate Descent for Diagonally Constrained SDPs

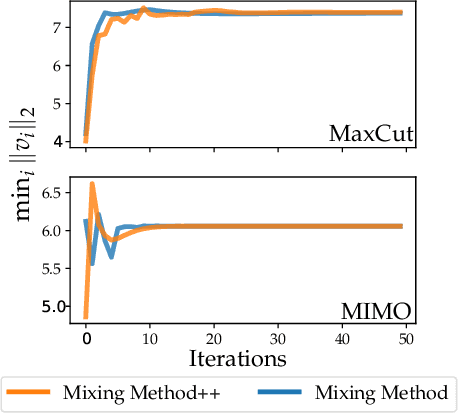
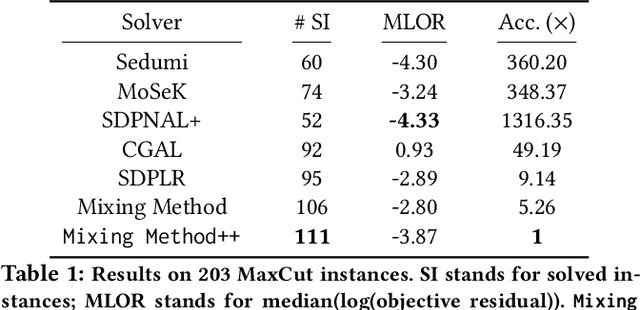
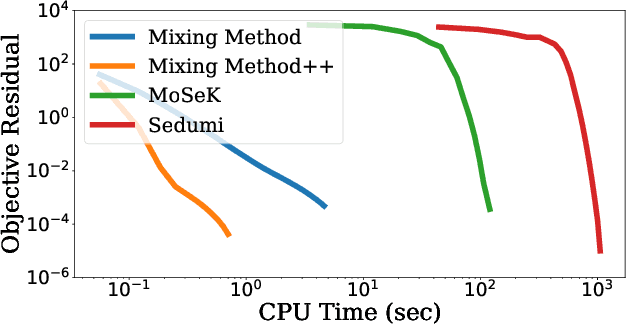
We present a novel, practical, and provable approach for solving diagonally constrained semi-definite programming (SDP) problems at scale using accelerated non-convex programming. Our algorithm non-trivially combines acceleration motions from convex optimization with coordinate power iteration and matrix factorization techniques. The algorithm is extremely simple to implement, and adds only a single extra hyperparameter -- momentum. We prove that our method admits local linear convergence in the neighborhood of the optimum and always converges to a first-order critical point. Experimentally, we showcase the merits of our method on three major application domains: MaxCut, MaxSAT, and MIMO signal detection. In all cases, our methodology provides significant speedups over non-convex and convex SDP solvers -- 5X faster than state-of-the-art non-convex solvers, and 9 to 10^3 X faster than convex SDP solvers -- with comparable or improved solution quality.