Scalable Average Consensus with Compressed Communications
Paper and Code
Sep 14, 2021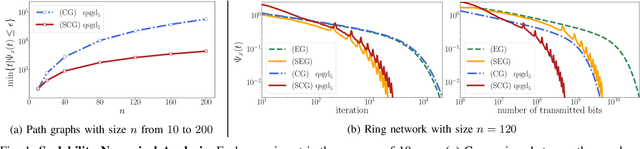
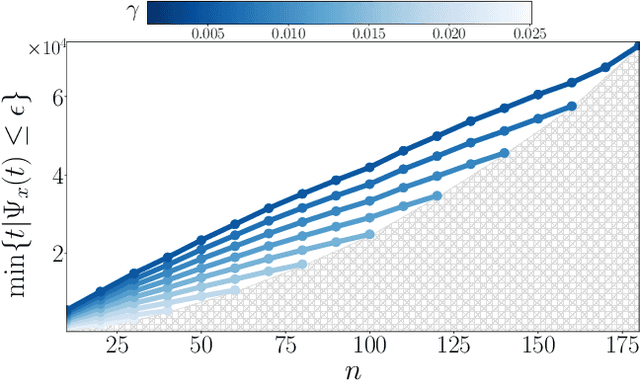

We propose a new decentralized average consensus algorithm with compressed communication that scales linearly with the network size n. We prove that the proposed method converges to the average of the initial values held locally by the agents of a network when agents are allowed to communicate with compressed messages. The proposed algorithm works for a broad class of compression operators (possibly biased), where agents interact over arbitrary static, undirected, and connected networks. We further present numerical experiments that confirm our theoretical results and illustrate the scalability and communication efficiency of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge