Fine-tuning Neural-Operator architectures for training and generalization

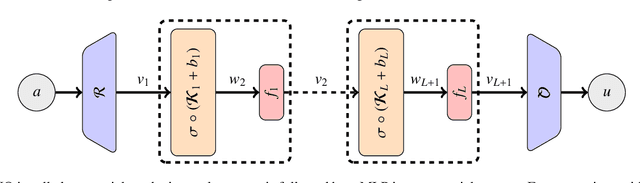
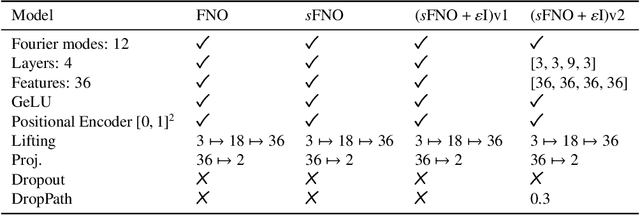
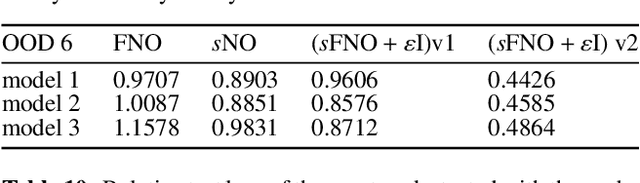
In this work, we present an analysis of the generalization of Neural Operators (NOs) and derived architectures. We proposed a family of networks, which we name (${\textit{s}}{\text{NO}}+\varepsilon$), where we modify the layout of NOs towards an architecture resembling a Transformer; mainly, we substitute the Attention module with the Integral Operator part of NOs. The resulting network preserves universality, has a better generalization to unseen data, and similar number of parameters as NOs. On the one hand, we study numerically the generalization by gradually transforming NOs into ${\textit{s}}{\text{NO}}+\varepsilon$ and verifying a reduction of the test loss considering a time-harmonic wave dataset with different frequencies. We perform the following changes in NOs: (a) we split the Integral Operator (non-local) and the (local) feed-forward network (MLP) into different layers, generating a {\it sequential} structure which we call sequential Neural Operator (${\textit{s}}{\text{NO}}$), (b) we add the skip connection, and layer normalization in ${\textit{s}}{\text{NO}}$, and (c) we incorporate dropout and stochastic depth that allows us to generate deep networks. In each case, we observe a decrease in the test loss in a wide variety of initialization, indicating that our changes outperform the NO. On the other hand, building on infinite-dimensional Statistics, and in particular the Dudley Theorem, we provide bounds of the Rademacher complexity of NOs and ${\textit{s}}{\text{NO}}$, and we find the following relationship: the upper bound of the Rademacher complexity of the ${\textit{s}}{\text{NO}}$ is a lower-bound of the NOs, thereby, the generalization error bound of ${\textit{s}}{\text{NO}}$ is smaller than NO, which further strengthens our numerical results.

Momentum-inspired Low-Rank Coordinate Descent for Diagonally Constrained SDPs

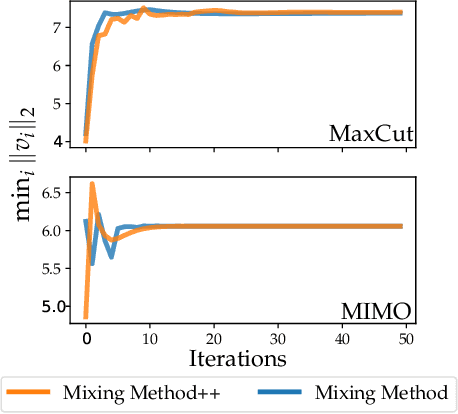
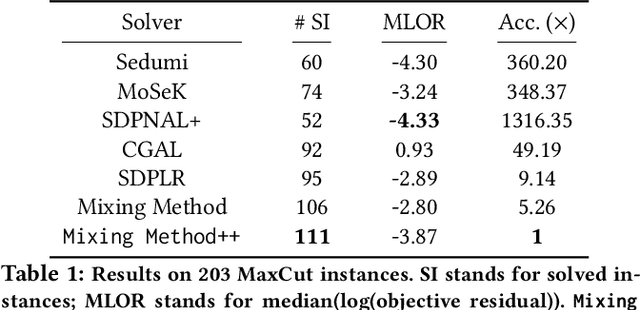
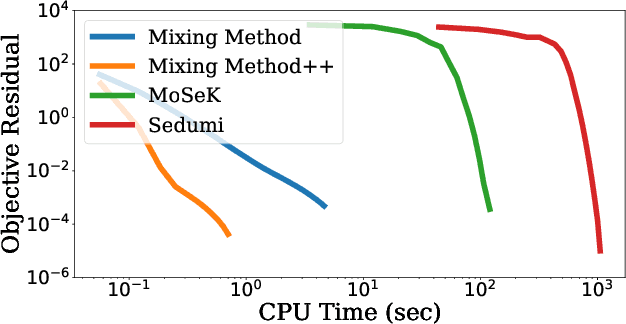
We present a novel, practical, and provable approach for solving diagonally constrained semi-definite programming (SDP) problems at scale using accelerated non-convex programming. Our algorithm non-trivially combines acceleration motions from convex optimization with coordinate power iteration and matrix factorization techniques. The algorithm is extremely simple to implement, and adds only a single extra hyperparameter -- momentum. We prove that our method admits local linear convergence in the neighborhood of the optimum and always converges to a first-order critical point. Experimentally, we showcase the merits of our method on three major application domains: MaxCut, MaxSAT, and MIMO signal detection. In all cases, our methodology provides significant speedups over non-convex and convex SDP solvers -- 5X faster than state-of-the-art non-convex solvers, and 9 to 10^3 X faster than convex SDP solvers -- with comparable or improved solution quality.