Soomin Lee
PersA-FL: Personalized Asynchronous Federated Learning
Oct 03, 2022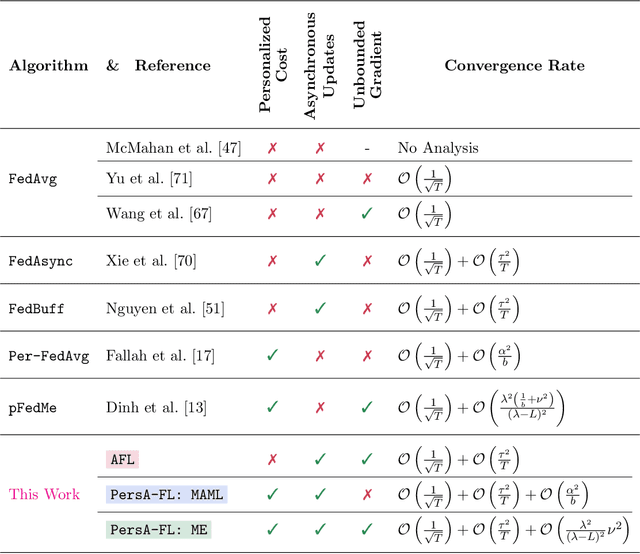
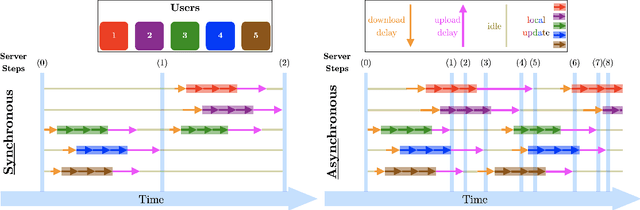

Abstract:We study the personalized federated learning problem under asynchronous updates. In this problem, each client seeks to obtain a personalized model that simultaneously outperforms local and global models. We consider two optimization-based frameworks for personalization: (i) Model-Agnostic Meta-Learning (MAML) and (ii) Moreau Envelope (ME). MAML involves learning a joint model adapted for each client through fine-tuning, whereas ME requires a bi-level optimization problem with implicit gradients to enforce personalization via regularized losses. We focus on improving the scalability of personalized federated learning by removing the synchronous communication assumption. Moreover, we extend the studied function class by removing boundedness assumptions on the gradient norm. Our main technical contribution is a unified proof for asynchronous federated learning with bounded staleness that we apply to MAML and ME personalization frameworks. For the smooth and non-convex functions class, we show the convergence of our method to a first-order stationary point. We illustrate the performance of our method and its tolerance to staleness through experiments for classification tasks over heterogeneous datasets.
Uncertainty Guided Policy for Active Robotic 3D Reconstruction using Neural Radiance Fields
Sep 17, 2022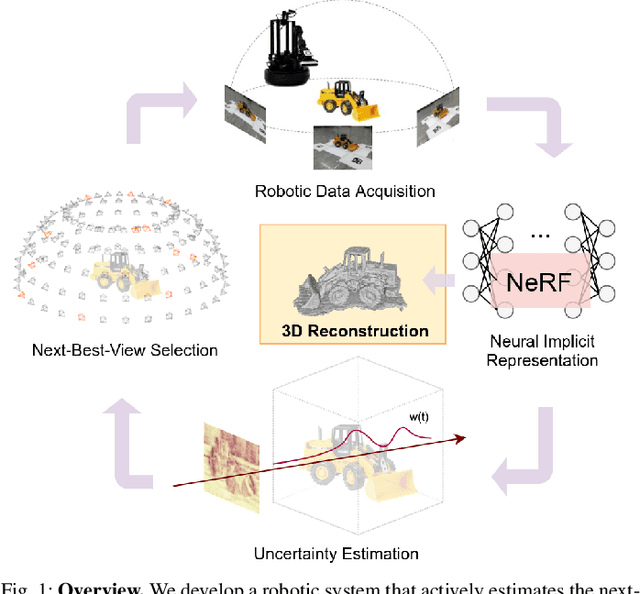
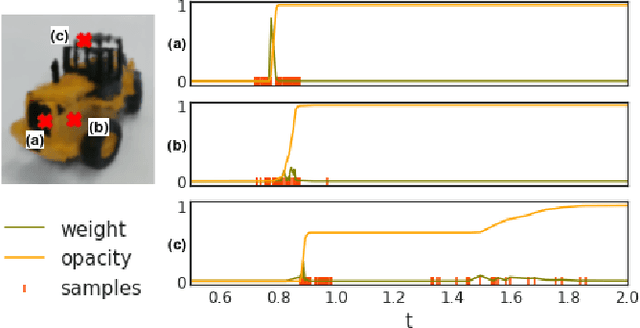

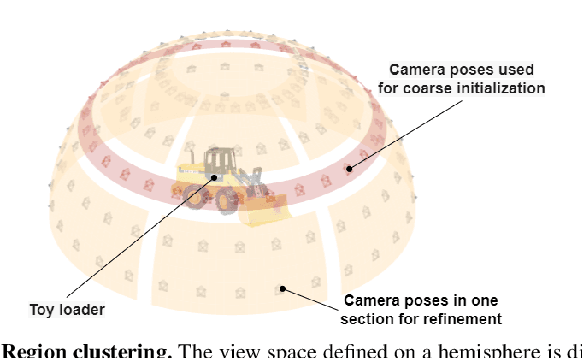
Abstract:In this paper, we tackle the problem of active robotic 3D reconstruction of an object. In particular, we study how a mobile robot with an arm-held camera can select a favorable number of views to recover an object's 3D shape efficiently. Contrary to the existing solution to this problem, we leverage the popular neural radiance fields-based object representation, which has recently shown impressive results for various computer vision tasks. However, it is not straightforward to directly reason about an object's explicit 3D geometric details using such a representation, making the next-best-view selection problem for dense 3D reconstruction challenging. This paper introduces a ray-based volumetric uncertainty estimator, which computes the entropy of the weight distribution of the color samples along each ray of the object's implicit neural representation. We show that it is possible to infer the uncertainty of the underlying 3D geometry given a novel view with the proposed estimator. We then present a next-best-view selection policy guided by the ray-based volumetric uncertainty in neural radiance fields-based representations. Encouraging experimental results on synthetic and real-world data suggest that the approach presented in this paper can enable a new research direction of using an implicit 3D object representation for the next-best-view problem in robot vision applications, distinguishing our approach from the existing approaches that rely on explicit 3D geometric modeling.
Select, Extract and Generate: Neural Keyphrase Generation with Syntactic Guidance
Aug 04, 2020
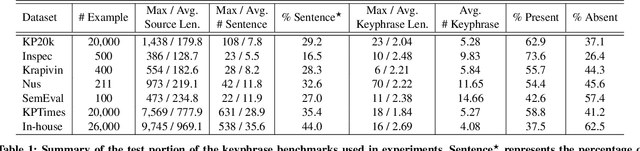


Abstract:In recent years, deep neural sequence-to-sequence framework has demonstrated promising results in keyphrase generation. However, processing long documents using such deep neural networks requires high computational resources. To reduce the computational cost, the documents are typically truncated before given as inputs. As a result, the models may miss essential points conveyed in a document. Moreover, most of the existing methods are either extractive (identify important phrases from the document) or generative (generate phrases word by word), and hence they do not benefit from the advantages of both modeling techniques. To address these challenges, we propose \emph{SEG-Net}, a neural keyphrase generation model that is composed of two major components, (1) a selector that selects the salient sentences in a document, and (2) an extractor-generator that jointly extracts and generates keyphrases from the selected sentences. SEG-Net uses a self-attentive architecture, known as, \emph{Transformer} as the building block with a couple of uniqueness. First, SEG-Net incorporates a novel \emph{layer-wise} coverage attention to summarize most of the points discussed in the target document. Second, it uses an \emph{informed} copy attention mechanism to encourage focusing on different segments of the document during keyphrase extraction and generation. Besides, SEG-Net jointly learns keyphrase generation and their part-of-speech tag prediction, where the later provides syntactic supervision to the former. The experimental results on seven keyphrase generation benchmarks from scientific and web documents demonstrate that SEG-Net outperforms the state-of-the-art neural generative methods by a large margin in both domains.
Optimal Algorithms for Distributed Optimization
Sep 05, 2018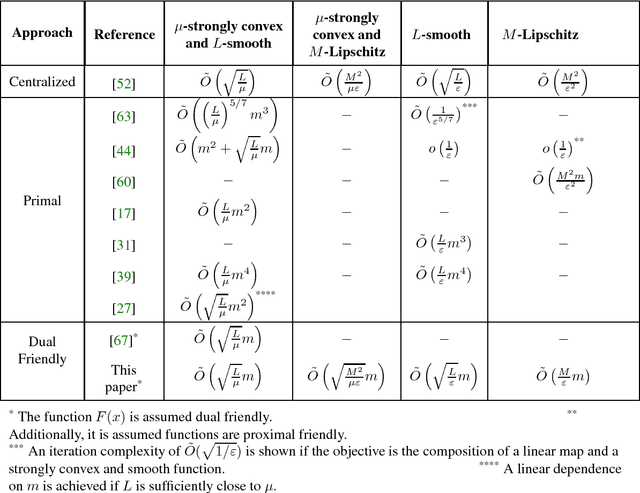

Abstract:In this paper, we study the optimal convergence rate for distributed convex optimization problems in networks. We model the communication restrictions imposed by the network as a set of affine constraints and provide optimal complexity bounds for four different setups, namely: the function $F(\xb) \triangleq \sum_{i=1}^{m}f_i(\xb)$ is strongly convex and smooth, either strongly convex or smooth or just convex. Our results show that Nesterov's accelerated gradient descent on the dual problem can be executed in a distributed manner and obtains the same optimal rates as in the centralized version of the problem (up to constant or logarithmic factors) with an additional cost related to the spectral gap of the interaction matrix. Finally, we discuss some extensions to the proposed setup such as proximal friendly functions, time-varying graphs, improvement of the condition numbers.
A Dual Approach for Optimal Algorithms in Distributed Optimization over Networks
Sep 03, 2018

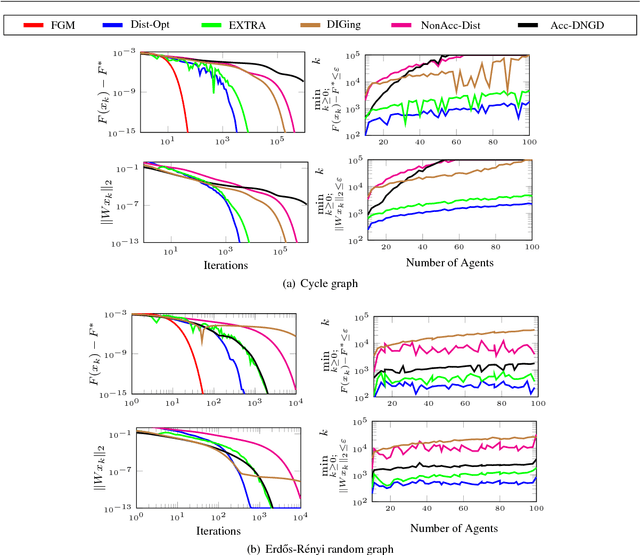
Abstract:We study the optimal convergence rates for distributed convex optimization problems over networks, where the objective is to minimize the sum $\sum_{i=1}^{m}f_i(z)$ of local functions of the nodes in the network. We provide optimal complexity bounds for four different cases, namely: the case when each function $f_i$ is strongly convex and smooth, the cases when it is either strongly convex or smooth and the case when it is convex but neither strongly convex nor smooth. Our approach is based on the dual of an appropriately formulated primal problem, which includes the underlying static graph that models the communication restrictions. Our results show distributed algorithms that achieve the same optimal rates as their centralized counterparts (up to constant and logarithmic factors), with an additional cost related to the spectral gap of the interaction matrix that captures the local communications of the nodes in the network.
Distributed Active State Estimation with User-Specified Accuracy
Jan 14, 2018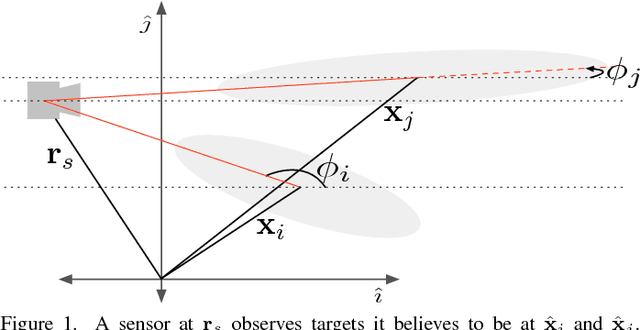
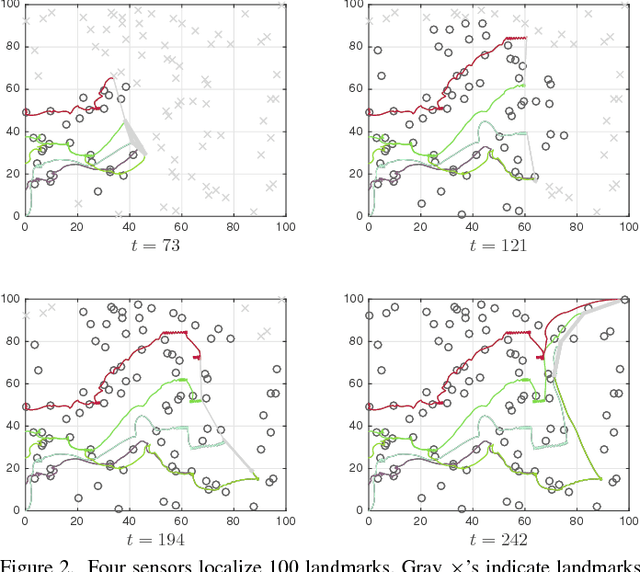
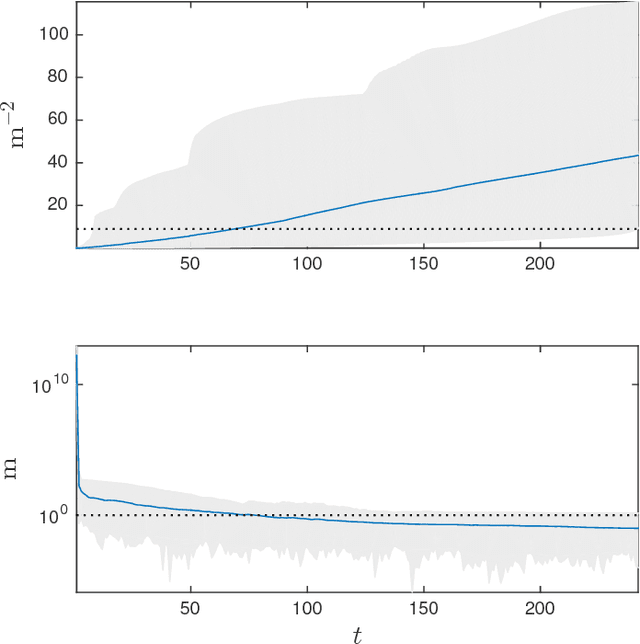
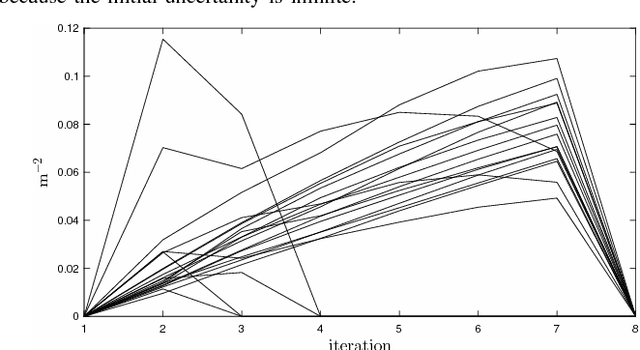
Abstract:In this paper, we address the problem of controlling a network of mobile sensors so that a set of hidden states are estimated up to a user-specified accuracy. The sensors take measurements and fuse them online using an Information Consensus Filter (ICF). At the same time, the local estimates guide the sensors to their next best configuration. This leads to an LMI-constrained optimization problem that we solve by means of a new distributed random approximate projections method. The new method is robust to the state disagreement errors that exist among the robots as the ICF fuses the collected measurements. Assuming that the noise corrupting the measurements is zero-mean and Gaussian and that the robots are self localized in the environment, the integrated system converges to the next best positions from where new observations will be taken. This process is repeated with the robots taking a sequence of observations until the hidden states are estimated up to the desired user-specified accuracy. We present simulations of sparse landmark localization, where the robotic team achieves the desired estimation tolerances while exhibiting interesting emergent behavior.
Communication-Efficient Algorithms for Decentralized and Stochastic Optimization
Feb 04, 2017Abstract:We present a new class of decentralized first-order methods for nonsmooth and stochastic optimization problems defined over multiagent networks. Considering that communication is a major bottleneck in decentralized optimization, our main goal in this paper is to develop algorithmic frameworks which can significantly reduce the number of inter-node communications. We first propose a decentralized primal-dual method which can find an $\epsilon$-solution both in terms of functional optimality gap and feasibility residual in $O(1/\epsilon)$ inter-node communication rounds when the objective functions are convex and the local primal subproblems are solved exactly. Our major contribution is to present a new class of decentralized primal-dual type algorithms, namely the decentralized communication sliding (DCS) methods, which can skip the inter-node communications while agents solve the primal subproblems iteratively through linearizations of their local objective functions. By employing DCS, agents can still find an $\epsilon$-solution in $O(1/\epsilon)$ (resp., $O(1/\sqrt{\epsilon})$) communication rounds for general convex functions (resp., strongly convex functions), while maintaining the $O(1/\epsilon^2)$ (resp., $O(1/\epsilon)$) bound on the total number of intra-node subgradient evaluations. We also present a stochastic counterpart for these algorithms, denoted by SDCS, for solving stochastic optimization problems whose objective function cannot be evaluated exactly. In comparison with existing results for decentralized nonsmooth and stochastic optimization, we can reduce the total number of inter-node communication rounds by orders of magnitude while still maintaining the optimal complexity bounds on intra-node stochastic subgradient evaluations. The bounds on the subgradient evaluations are actually comparable to those required for centralized nonsmooth and stochastic optimization.
Coordinate Dual Averaging for Decentralized Online Optimization with Nonseparable Global Objectives
May 20, 2016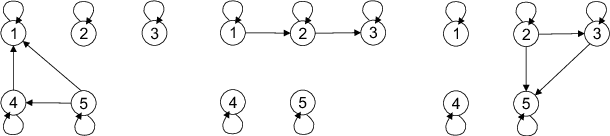
Abstract:We consider a decentralized online convex optimization problem in a network of agents, where each agent controls only a coordinate (or a part) of the global decision vector. For such a problem, we propose two decentralized variants (ODA-C and ODA-PS) of Nesterov's primal-dual algorithm with dual averaging. In ODA-C, to mitigate the disagreements on the primal-vector updates, the agents implement a generalization of the local information-exchange dynamics recently proposed by Li and Marden over a static undirected graph. In ODA-PS, the agents implement the broadcast-based push-sum dynamics over a time-varying sequence of uniformly connected digraphs. We show that the regret bounds in both cases have sublinear growth of $O(\sqrt{T})$, with the time horizon $T$, when the stepsize is of the form $1/\sqrt{t}$ and the objective functions are Lipschitz-continuous convex functions with Lipschitz gradients. We also implement the proposed algorithms on a sensor network to complement our theoretical analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge