A Dual Approach for Optimal Algorithms in Distributed Optimization over Networks

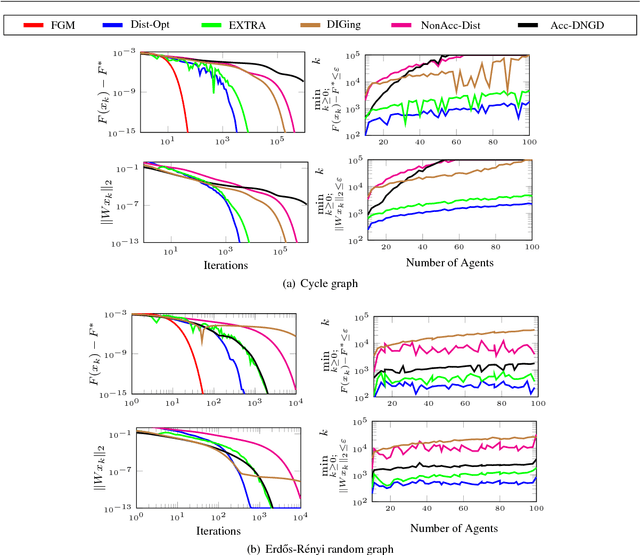
We study the optimal convergence rates for distributed convex optimization problems over networks, where the objective is to minimize the sum $\sum_{i=1}^{m}f_i(z)$ of local functions of the nodes in the network. We provide optimal complexity bounds for four different cases, namely: the case when each function $f_i$ is strongly convex and smooth, the cases when it is either strongly convex or smooth and the case when it is convex but neither strongly convex nor smooth. Our approach is based on the dual of an appropriately formulated primal problem, which includes the underlying static graph that models the communication restrictions. Our results show distributed algorithms that achieve the same optimal rates as their centralized counterparts (up to constant and logarithmic factors), with an additional cost related to the spectral gap of the interaction matrix that captures the local communications of the nodes in the network.