Fast Distributed Optimization over Directed Graphs under Malicious Attacks using Trust

In this work, we introduce the Resilient Projected Push-Pull (RP3) algorithm designed for distributed optimization in multi-agent cyber-physical systems with directed communication graphs and the presence of malicious agents. Our algorithm leverages stochastic inter-agent trust values and gradient tracking to achieve geometric convergence rates in expectation even in adversarial environments. We introduce growing constraint sets to limit the impact of the malicious agents without compromising the geometric convergence rate of the algorithm. We prove that RP3 converges to the nominal optimal solution almost surely and in the $r$-th mean for any $r\geq 1$, provided the step sizes are sufficiently small and the constraint sets are appropriately chosen. We validate our approach with numerical studies on average consensus and multi-robot target tracking problems, demonstrating that RP3 effectively mitigates the impact of malicious agents and achieves the desired geometric convergence.

How Physicality Enables Trust: A New Era of Trust-Centered Cyberphysical Systems

Multi-agent cyberphysical systems enable new capabilities in efficiency, resilience, and security. The unique characteristics of these systems prompt a reevaluation of their security concepts, including their vulnerabilities, and mechanisms to mitigate these vulnerabilities. This survey paper examines how advancement in wireless networking, coupled with the sensing and computing in cyberphysical systems, can foster novel security capabilities. This study delves into three main themes related to securing multi-agent cyberphysical systems. First, we discuss the threats that are particularly relevant to multi-agent cyberphysical systems given the potential lack of trust between agents. Second, we present prospects for sensing, contextual awareness, and authentication, enabling the inference and measurement of ``inter-agent trust" for these systems. Third, we elaborate on the application of quantifiable trust notions to enable ``resilient coordination," where ``resilient" signifies sustained functionality amid attacks on multiagent cyberphysical systems. We refer to the capability of cyberphysical systems to self-organize, and coordinate to achieve a task as autonomy. This survey unveils the cyberphysical character of future interconnected systems as a pivotal catalyst for realizing robust, trust-centered autonomy in tomorrow's world.

Resilient Distributed Optimization for Multi-Agent Cyberphysical Systems

Enhancing resilience in distributed networks in the face of malicious agents is an important problem for which many key theoretical results and applications require further development and characterization. This work focuses on the problem of distributed optimization in multi-agent cyberphysical systems, where a legitimate agent's dynamic is influenced both by the values it receives from potentially malicious neighboring agents, and by its own self-serving target function. We develop a new algorithmic and analytical framework to achieve resilience for the class of problems where stochastic values of trust between agents exist and can be exploited. In this case we show that convergence to the true global optimal point can be recovered, both in mean and almost surely, even in the presence of malicious agents. Furthermore, we provide expected convergence rate guarantees in the form of upper bounds on the expected squared distance to the optimal value. Finally, we present numerical results that validate the analytical convergence guarantees we present in this paper even when the malicious agents compose the majority of agents in the network.

Characterizing Trust and Resilience in Distributed Consensus for Cyberphysical Systems

This work considers the problem of resilient consensus where stochastic values of trust between agents are available. Specifically, we derive a unified mathematical framework to characterize convergence, deviation of the consensus from the true consensus value, and expected convergence rate, when there exists additional information of trust between agents. We show that under certain conditions on the stochastic trust values and consensus protocol: 1) almost sure convergence to a common limit value is possible even when malicious agents constitute more than half of the network connectivity, 2) the deviation of the converged limit, from the case where there is no attack, i.e., the true consensus value, can be bounded with probability that approaches 1 exponentially, and 3) correct classification of malicious and legitimate agents can be attained in finite time almost surely. Further, the expected convergence rate decays exponentially with the quality of the trust observations between agents.

A general framework for decentralized optimization with first-order methods

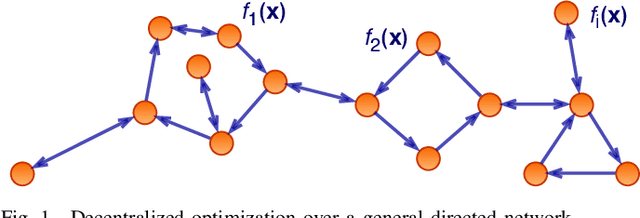
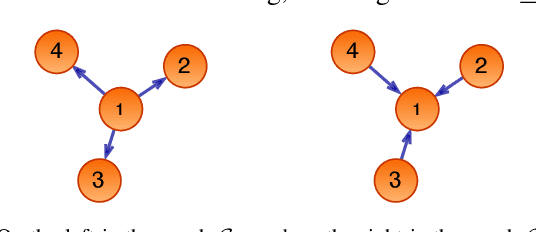
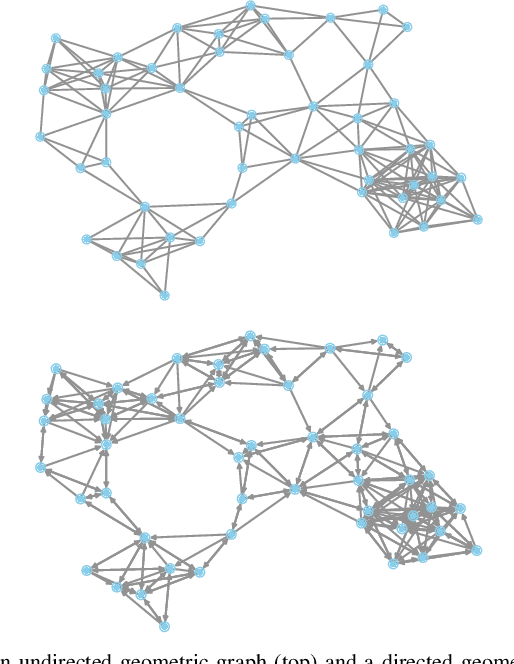
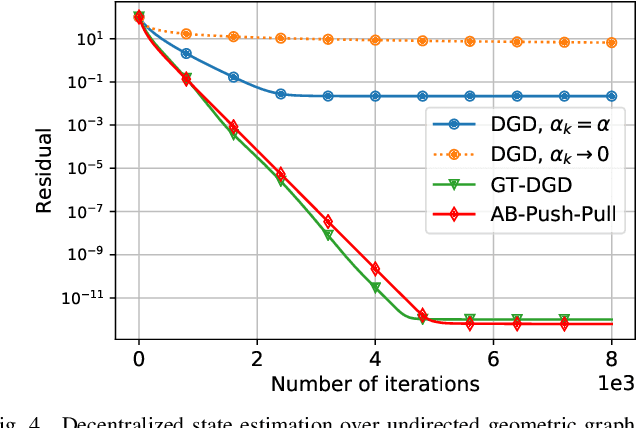
Decentralized optimization to minimize a finite sum of functions over a network of nodes has been a significant focus within control and signal processing research due to its natural relevance to optimal control and signal estimation problems. More recently, the emergence of sophisticated computing and large-scale data science needs have led to a resurgence of activity in this area. In this article, we discuss decentralized first-order gradient methods, which have found tremendous success in control, signal processing, and machine learning problems, where such methods, due to their simplicity, serve as the first method of choice for many complex inference and training tasks. In particular, we provide a general framework of decentralized first-order methods that is applicable to undirected and directed communication networks alike, and show that much of the existing work on optimization and consensus can be related explicitly to this framework. We further extend the discussion to decentralized stochastic first-order methods that rely on stochastic gradients at each node and describe how local variance reduction schemes, previously shown to have promise in the centralized settings, are able to improve the performance of decentralized methods when combined with what is known as gradient tracking. We motivate and demonstrate the effectiveness of the corresponding methods in the context of machine learning and signal processing problems that arise in decentralized environments.

On the Sample Complexity and Optimization Landscape for Quadratic Feasibility Problems

We consider the problem of recovering a complex vector $\mathbf{x}\in \mathbb{C}^n$ from $m$ quadratic measurements $\{\langle A_i\mathbf{x}, \mathbf{x}\rangle\}_{i=1}^m$. This problem, known as quadratic feasibility, encompasses the well known phase retrieval problem and has applications in a wide range of important areas including power system state estimation and x-ray crystallography. In general, not only is the the quadratic feasibility problem NP-hard to solve, but it may in fact be unidentifiable. In this paper, we establish conditions under which this problem becomes {identifiable}, and further prove isometry properties in the case when the matrices $\{A_i\}_{i=1}^m$ are Hermitian matrices sampled from a complex Gaussian distribution. Moreover, we explore a nonconvex {optimization} formulation of this problem, and establish salient features of the associated optimization landscape that enables gradient algorithms with an arbitrary initialization to converge to a \emph{globally optimal} point with a high probability. Our results also reveal sample complexity requirements for successfully identifying a feasible solution in these contexts.

Distributed Computation of Wasserstein Barycenters over Networks

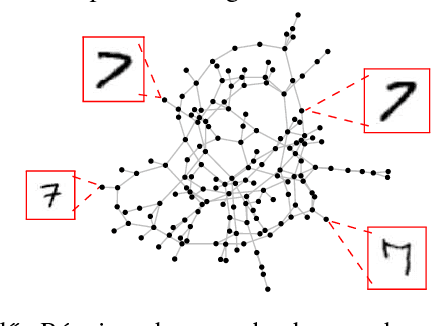
We propose a new \cu{class-optimal} algorithm for the distributed computation of Wasserstein Barycenters over networks. Assuming that each node in a graph has a probability distribution, we prove that every node can reach the barycenter of all distributions held in the network by using local interactions compliant with the topology of the graph. We provide an estimate for the minimum number of communication rounds required for the proposed method to achieve arbitrary relative precision both in the optimality of the solution and the consensus among all agents for undirected fixed networks.

Distributed Stochastic Gradient Tracking Methods

In this paper, we study the problem of distributed multi-agent optimization over a network, where each agent possesses a local cost function that is smooth and strongly convex. The global objective is to find a common solution that minimizes the average of all cost functions. Assuming agents only have access to unbiased estimates of the gradients of their local cost functions, we consider a distributed stochastic gradient tracking method (DSGT) and a gossip-like stochastic gradient tracking method (GSGT). We show that, in expectation, the iterates generated by each agent are attracted to a neighborhood of the optimal solution, where they accumulate exponentially fast (under a constant stepsize choice). Under DSGT, the limiting (expected) error bounds on the distance of the iterates from the optimal solution decrease with the network size $n$, which is a comparable performance to a centralized stochastic gradient algorithm. Moreover, we show that when the network is well-connected, GSGT incurs lower communication cost than DSGT while maintaining a similar computational cost. Numerical example further demonstrates the effectiveness of the proposed methods.

Optimal Algorithms for Distributed Optimization

In this paper, we study the optimal convergence rate for distributed convex optimization problems in networks. We model the communication restrictions imposed by the network as a set of affine constraints and provide optimal complexity bounds for four different setups, namely: the function $F(\xb) \triangleq \sum_{i=1}^{m}f_i(\xb)$ is strongly convex and smooth, either strongly convex or smooth or just convex. Our results show that Nesterov's accelerated gradient descent on the dual problem can be executed in a distributed manner and obtains the same optimal rates as in the centralized version of the problem (up to constant or logarithmic factors) with an additional cost related to the spectral gap of the interaction matrix. Finally, we discuss some extensions to the proposed setup such as proximal friendly functions, time-varying graphs, improvement of the condition numbers.

A Dual Approach for Optimal Algorithms in Distributed Optimization over Networks

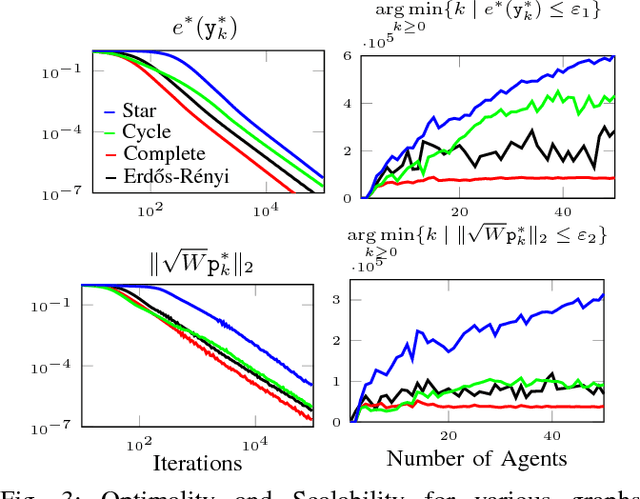
We study the optimal convergence rates for distributed convex optimization problems over networks, where the objective is to minimize the sum $\sum_{i=1}^{m}f_i(z)$ of local functions of the nodes in the network. We provide optimal complexity bounds for four different cases, namely: the case when each function $f_i$ is strongly convex and smooth, the cases when it is either strongly convex or smooth and the case when it is convex but neither strongly convex nor smooth. Our approach is based on the dual of an appropriately formulated primal problem, which includes the underlying static graph that models the communication restrictions. Our results show distributed algorithms that achieve the same optimal rates as their centralized counterparts (up to constant and logarithmic factors), with an additional cost related to the spectral gap of the interaction matrix that captures the local communications of the nodes in the network.