Distributed Computation of Wasserstein Barycenters over Networks
Paper and Code
Sep 20, 2018
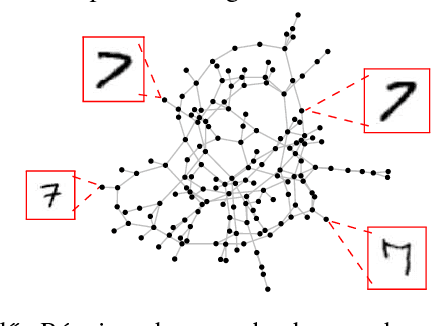
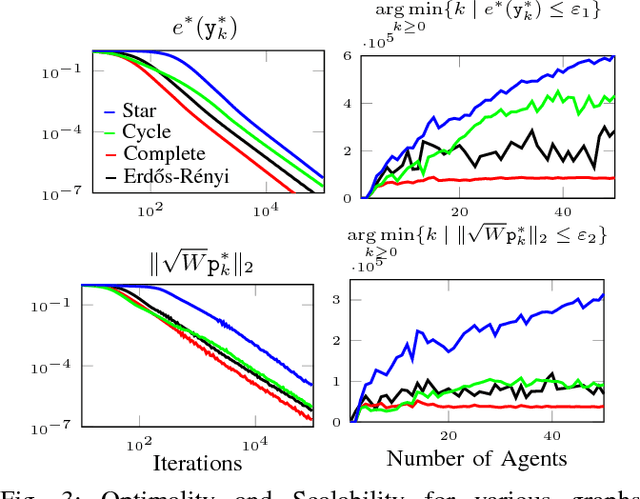

We propose a new \cu{class-optimal} algorithm for the distributed computation of Wasserstein Barycenters over networks. Assuming that each node in a graph has a probability distribution, we prove that every node can reach the barycenter of all distributions held in the network by using local interactions compliant with the topology of the graph. We provide an estimate for the minimum number of communication rounds required for the proposed method to achieve arbitrary relative precision both in the optimality of the solution and the consensus among all agents for undirected fixed networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge