Accelerated zero-order SGD under high-order smoothness and overparameterized regime

We present a novel gradient-free algorithm to solve a convex stochastic optimization problem, such as those encountered in medicine, physics, and machine learning (e.g., adversarial multi-armed bandit problem), where the objective function can only be computed through numerical simulation, either as the result of a real experiment or as feedback given by the function evaluations from an adversary. Thus we suppose that only a black-box access to the function values of the objective is available, possibly corrupted by adversarial noise: deterministic or stochastic. The noisy setup can arise naturally from modeling randomness within a simulation or by computer discretization, or when exact values of function are forbidden due to privacy issues, or when solving non-convex problems as convex ones with an inexact function oracle. By exploiting higher-order smoothness, fulfilled, e.g., in logistic regression, we improve the performance of zero-order methods developed under the assumption of classical smoothness (or having a Lipschitz gradient). The proposed algorithm enjoys optimal oracle complexity and is designed under an overparameterization setup, i.e., when the number of model parameters is much larger than the size of the training dataset. Overparametrized models fit to the training data perfectly while also having good generalization and outperforming underparameterized models on unseen data. We provide convergence guarantees for the proposed algorithm under both types of noise. Moreover, we estimate the maximum permissible adversarial noise level that maintains the desired accuracy in the Euclidean setup, and then we extend our results to a non-Euclidean setup. Our theoretical results are verified on the logistic regression problem.

SA vs SAA for population Wasserstein barycenter calculation

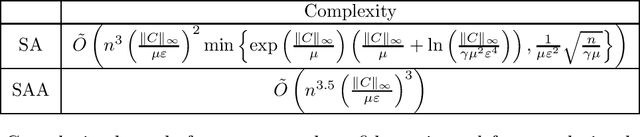
In Machine Learning and Optimization community there are two main approaches for convex risk minimization problem. The first approach is Stochastic Averaging (SA) (online) and the second one is Stochastic Average Approximation (SAA) (Monte Carlo, Empirical Risk Minimization, offline) with proper regularization in non-strongly convex case. At the moment, it is known that both approaches are on average equivalent (up to a logarithmic factor) in terms of oracle complexity (required number of stochastic gradient evaluations). What is the situation with total complexity? The answer depends on specific problem. However, starting from work [Nemirovski et al. (2009)] it was generally accepted that SA is better than SAA. Nevertheless, in case of large-scale problems SA may ran out of memory problems since storing all data on one machine and organizing online access to it can be impossible without communications with other machines. SAA in contradistinction to SA allows parallel/distributed calculations. In this paper we show that SAA may outperform SA in the problem of calculating an estimation for population ({\mu}-entropy regularized) Wasserstein barycenter even for non-parallel (non-decenralized) set up.

Distributed Computation of Wasserstein Barycenters over Networks

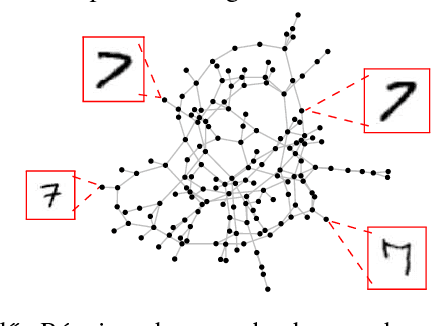
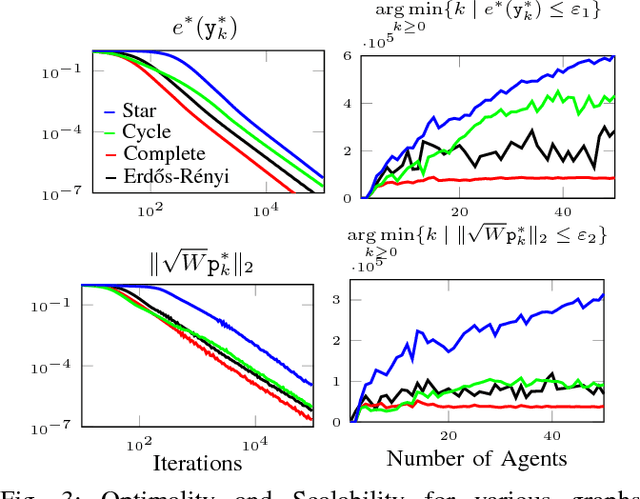
We propose a new \cu{class-optimal} algorithm for the distributed computation of Wasserstein Barycenters over networks. Assuming that each node in a graph has a probability distribution, we prove that every node can reach the barycenter of all distributions held in the network by using local interactions compliant with the topology of the graph. We provide an estimate for the minimum number of communication rounds required for the proposed method to achieve arbitrary relative precision both in the optimality of the solution and the consensus among all agents for undirected fixed networks.