BFS-Prover: Scalable Best-First Tree Search for LLM-based Automatic Theorem Proving

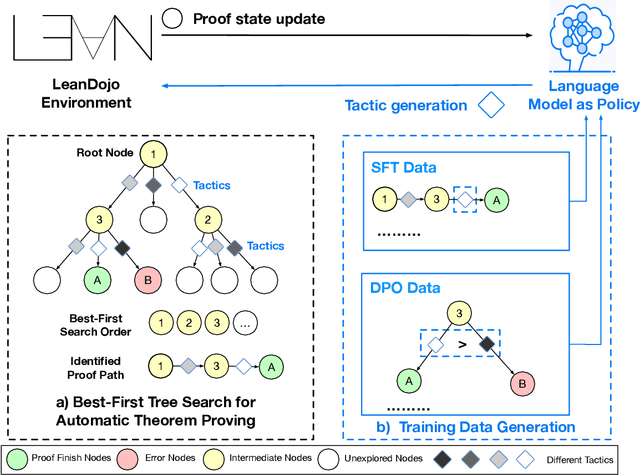
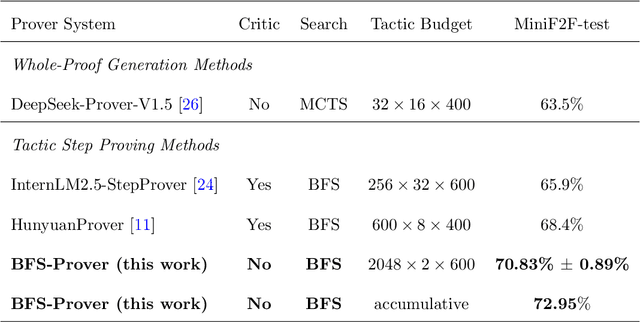
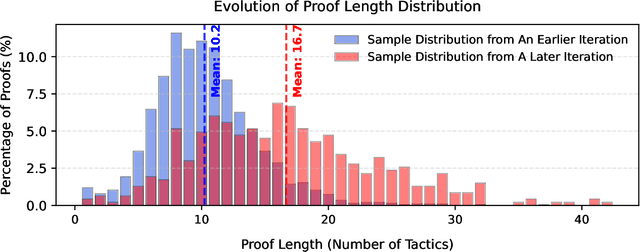
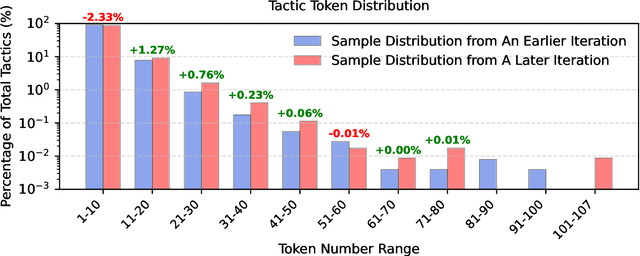
Recent advancements in large language models (LLMs) have spurred growing interest in automatic theorem proving using Lean4, where effective tree search methods are crucial for navigating proof search spaces. While the existing approaches primarily rely on value functions and Monte Carlo Tree Search (MCTS), the potential of simpler methods like Best-First Search (BFS) remains underexplored. This paper investigates whether BFS can achieve competitive performance in large-scale theorem proving tasks. We present \texttt{BFS-Prover}, a scalable expert iteration framework, featuring three key innovations. First, we implement strategic data filtering at each expert iteration round, excluding problems solvable via beam search node expansion to focus on harder cases. Second, we improve the sample efficiency of BFS through Direct Preference Optimization (DPO) applied to state-tactic pairs automatically annotated with compiler error feedback, refining the LLM's policy to prioritize productive expansions. Third, we employ length normalization in BFS to encourage exploration of deeper proof paths. \texttt{BFS-Prover} achieves a score of $71.31$ on the MiniF2F test set and therefore challenges the perceived necessity of complex tree search methods, demonstrating that BFS can achieve competitive performance when properly scaled.

Variance reduced stochastic optimization over directed graphs with row and column stochastic weights

This paper proposes AB-SAGA, a first-order distributed stochastic optimization method to minimize a finite-sum of smooth and strongly convex functions distributed over an arbitrary directed graph. AB-SAGA removes the uncertainty caused by the stochastic gradients using a node-level variance reduction and subsequently employs network-level gradient tracking to address the data dissimilarity across the nodes. Unlike existing methods that use the nonlinear push-sum correction to cancel the imbalance caused by the directed communication, the consensus updates in AB-SAGA are linear and uses both row and column stochastic weights. We show that for a constant step-size, AB-SAGA converges linearly to the global optimal. We quantify the directed nature of the underlying graph using an explicit directivity constant and characterize the regimes in which AB-SAGA achieves a linear speed-up over its centralized counterpart. Numerical experiments illustrate the convergence of AB-SAGA for strongly convex and nonconvex problems.

A hybrid variance-reduced method for decentralized stochastic non-convex optimization

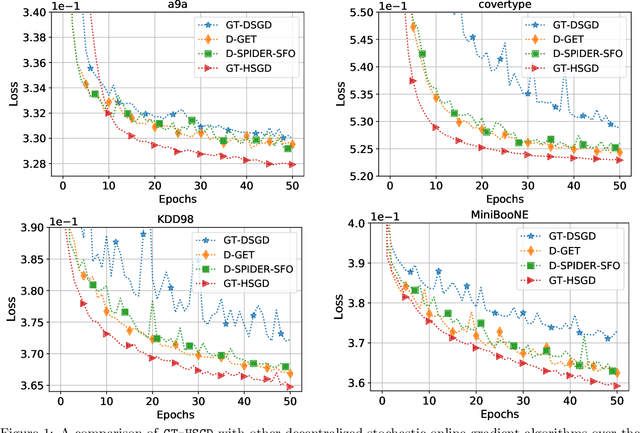
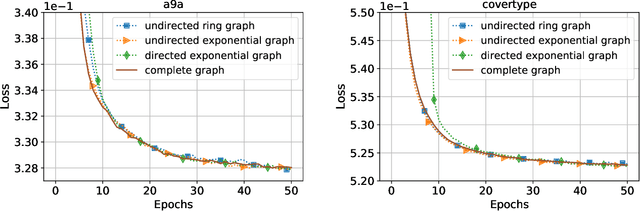
This paper considers decentralized stochastic optimization over a network of~$n$ nodes, where each node possesses a smooth non-convex local cost function and the goal of the networked nodes is to find an~$\epsilon$-accurate first-order stationary point of the sum of the local costs. We focus on an online setting, where each node accesses its local cost only by means of a stochastic first-order oracle that returns a noisy version of the exact gradient. In this context, we propose a novel single-loop decentralized hybrid variance-reduced stochastic gradient method, called \texttt{GT-HSGD}, that outperforms the existing approaches in terms of both the oracle complexity and practical implementation. The \texttt{GT-HSGD} algorithm implements specialized local hybrid stochastic gradient estimators that are fused over the network to track the global gradient. Remarkably, \texttt{GT-HSGD} achieves a network-independent oracle complexity of~$O(n^{-1}\epsilon^{-3})$ when the required error tolerance~$\epsilon$ is small enough, leading to a linear speedup with respect to the centralized optimal online variance-reduced approaches that operate on a single node. Numerical experiments are provided to illustrate our main technical results.

A fast randomized incremental gradient method for decentralized non-convex optimization

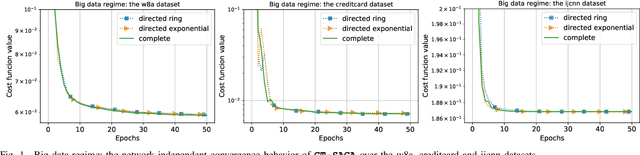
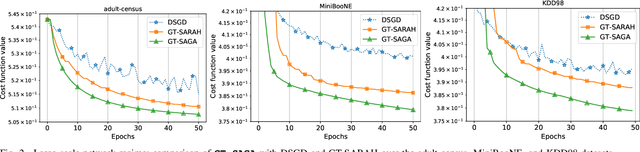
We study decentralized non-convex finite-sum minimization problems described over a network of nodes, where each node possesses a local batch of data samples. We propose a single-timescale first-order randomized incremental gradient method, termed as GT-SAGA. GT-SAGA is computationally efficient since it evaluates only one component gradient per node per iteration and achieves provably fast and robust performance by leveraging node-level variance reduction and network-level gradient tracking. For general smooth non-convex problems, we show almost sure and mean-squared convergence to a first-order stationary point and describe regimes of practical significance where GT-SAGA achieves a network-independent convergence rate and outperforms the existing approaches respectively. When the global cost function further satisfies the Polyak-Lojaciewisz condition, we show that GT-SAGA exhibits global linear convergence to an optimal solution in expectation and describe regimes of practical interest where the performance is network-independent and improves upon the existing work. Numerical experiments based on real-world datasets are included to highlight the behavior and convergence aspects of the proposed method.

A near-optimal stochastic gradient method for decentralized non-convex finite-sum optimization

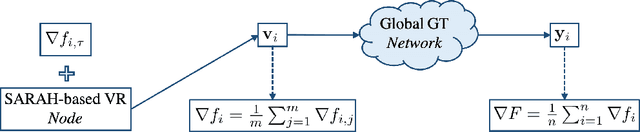
This paper describes a $near$-$optimal$ stochastic first-order gradient method for decentralized finite-sum minimization of smooth non-convex functions. Specifically, we propose GT-SARAH that employs a local SARAH-type variance reduction and global gradient tracking to address the stochastic and decentralized nature of the problem. Considering a total number of $N$ cost functions, equally divided over a directed network of $n$ nodes, we show that GT-SARAH finds an $\epsilon$-accurate first-order stationary point in ${\mathcal{O}(N^{1/2}\epsilon^{-1})}$ gradient computations across all nodes, independent of the network topology, when ${n\leq\mathcal{O}(N^{1/2}(1-\lambda)^{3})}$, where ${(1-\lambda)}$ is the spectral gap of the network weight matrix. In this regime, GT-SARAH is thus, to the best our knowledge, the first decentralized method that achieves the algorithmic lower bound for this class of problems. Moreover, GT-SARAH achieves a $non$-$asymptotic$ $linear$ $speedup$, in that, the total number of gradient computations at each node is reduced by a factor of $1/n$ compared to the near-optimal algorithms for this problem class that process all data at a single node. We also establish the convergence rate of GT-SARAH in other regimes, in terms of the relative sizes of the number of nodes $n$, total number of functions $N$, and the network spectral gap $(1-\lambda)$. Over infinite time horizon, we establish the almost sure and mean-squared convergence of GT-SARAH to a first-order stationary point.

A general framework for decentralized optimization with first-order methods

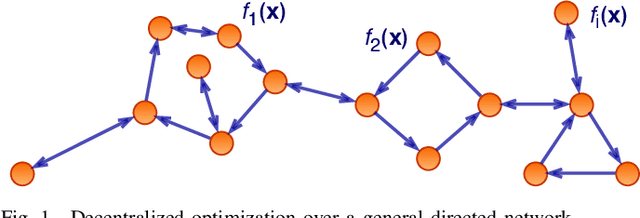
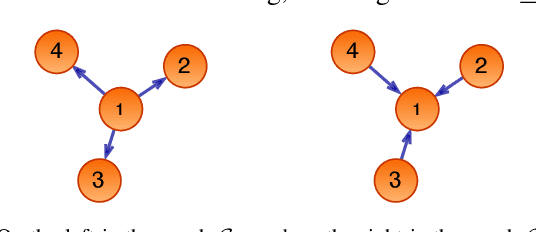
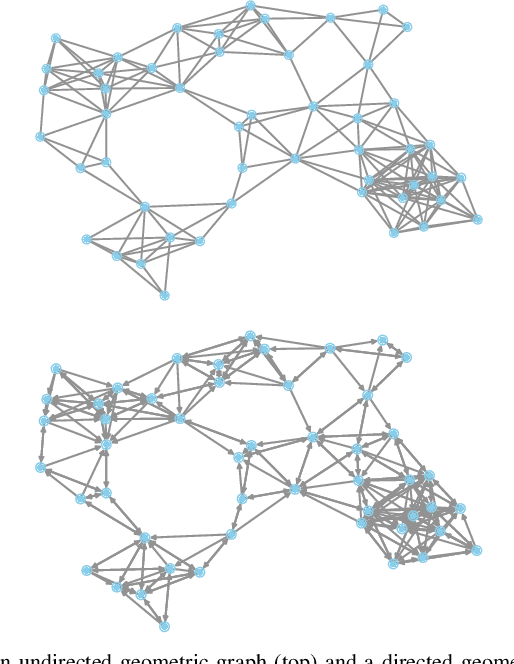
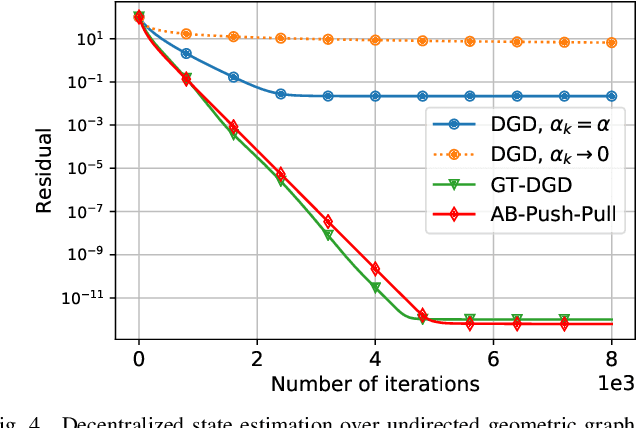
Decentralized optimization to minimize a finite sum of functions over a network of nodes has been a significant focus within control and signal processing research due to its natural relevance to optimal control and signal estimation problems. More recently, the emergence of sophisticated computing and large-scale data science needs have led to a resurgence of activity in this area. In this article, we discuss decentralized first-order gradient methods, which have found tremendous success in control, signal processing, and machine learning problems, where such methods, due to their simplicity, serve as the first method of choice for many complex inference and training tasks. In particular, we provide a general framework of decentralized first-order methods that is applicable to undirected and directed communication networks alike, and show that much of the existing work on optimization and consensus can be related explicitly to this framework. We further extend the discussion to decentralized stochastic first-order methods that rely on stochastic gradients at each node and describe how local variance reduction schemes, previously shown to have promise in the centralized settings, are able to improve the performance of decentralized methods when combined with what is known as gradient tracking. We motivate and demonstrate the effectiveness of the corresponding methods in the context of machine learning and signal processing problems that arise in decentralized environments.

Push-SAGA: A decentralized stochastic algorithm with variance reduction over directed graphs

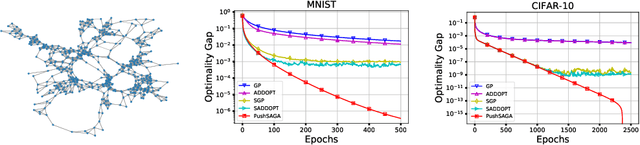
In this paper, we propose Push-SAGA, a decentralized stochastic first-order method for finite-sum minimization over a directed network of nodes. Push-SAGA combines node-level variance reduction to remove the uncertainty caused by stochastic gradients, network-level gradient tracking to address the distributed nature of the data, and push-sum consensus to tackle the challenge of directed communication links. We show that Push-SAGA achieves linear convergence to the exact solution for smooth and strongly convex problems and is thus the first linearly-convergent stochastic algorithm over arbitrary strongly connected directed graphs. We also characterize the regimes in which Push-SAGA achieves a linear speed-up compared to its centralized counterpart and achieves a network-independent convergence rate. We illustrate the behavior and convergence properties of Push-SAGA with the help of numerical experiments on strongly convex and non-convex problems.

An improved convergence analysis for decentralized online stochastic non-convex optimization

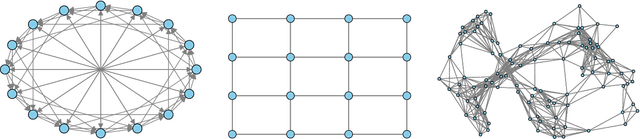
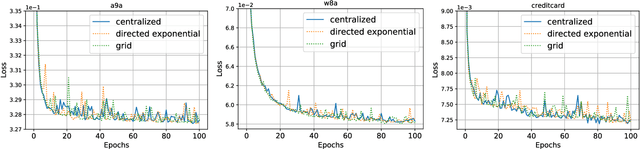
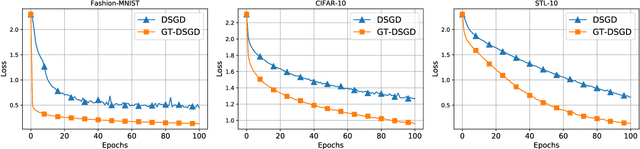
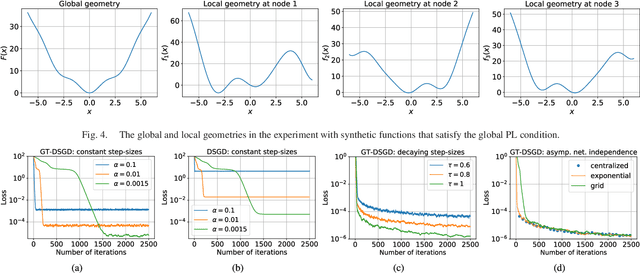
In this paper, we study decentralized online stochastic non-convex optimization over a network of nodes. Integrating a technique called gradient tracking in decentralized stochastic gradient descent (DSGD), we show that the resulting algorithm, GT-DSGD, exhibits several important characteristics towards minimizing a sum of smooth non-convex functions. The main results of this paper can be divided into two categories: (1) For general smooth non-convex functions, we establish a non-asymptotic characterization of GT-DSGD and derive the conditions under which it achieves network-independent performance and matches centralized minibatch SGD. In comparison, the existing results suggest that the performance of GT-DSGD is always network-dependent and is therefore strictly worse than that of centralized minibatch SGD. (2) When the global function additionally satisfies the Polyak-Lojasiewics condition, we derive the exponential stability range for GT-DSGD under a constant step-size up to a steady-state error. Under stochastic approximation step-sizes, we establish, for the first time, the optimal global sublinear convergence rate on almost every sample path, in addition to the convergence rate in mean. Since strongly convex functions are a special case of this class of problems, our results are not only immediately applicable but also improve the currently known best convergence rates and their dependence on problem parameters.

S-ADDOPT: Decentralized stochastic first-order optimization over directed graphs

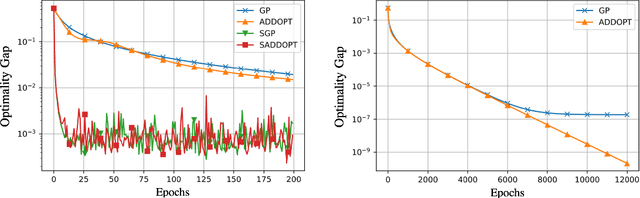
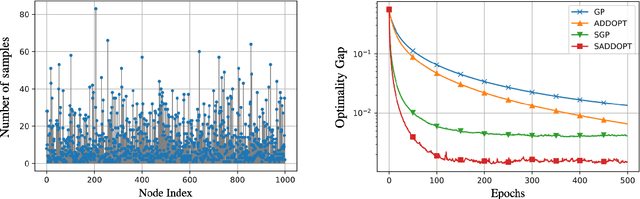
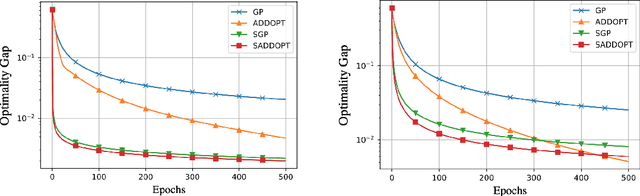
In this report, we study decentralized stochastic optimization to minimize a sum of smooth and strongly convex cost functions when the functions are distributed over a directed network of nodes. In contrast to the existing work, we use gradient tracking to improve certain aspects of the resulting algorithm. In particular, we propose the S-ADDOPT algorithm that assumes a stochastic first-order oracle at each node and show that for a constant step-size $\alpha$, each node converges linearly inside an error ball around the optimal solution, the size of which is controlled by $\alpha$. For decaying step-sizes $\mathcal{O}(1/k)$, we show that S-ADDOPT reaches the exact solution sublinearly at $\mathcal{O}(1/k)$ and its convergence is asymptotically network-independent. Thus the asymptotic behavior of S-ADDOPT is comparable to the centralized stochastic gradient descent. Numerical experiments over both strongly convex and non-convex problems illustrate the convergence behavior and the performance comparison of the proposed algorithm.

Gradient tracking and variance reduction for decentralized optimization and machine learning

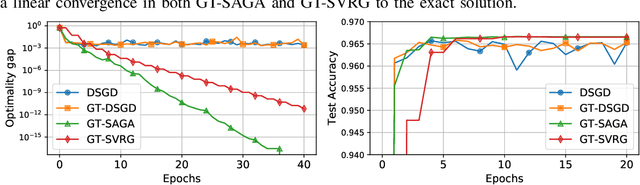
Decentralized methods to solve finite-sum minimization problems are important in many signal processing and machine learning tasks where the data is distributed over a network of nodes and raw data sharing is not permitted due to privacy and/or resource constraints. In this article, we review decentralized stochastic first-order methods and provide a unified algorithmic framework that combines variance-reduction with gradient tracking to achieve both robust performance and fast convergence. We provide explicit theoretical guarantees of the corresponding methods when the objective functions are smooth and strongly-convex, and show their applicability to non-convex problems via numerical experiments. Throughout the article, we provide intuitive illustrations of the main technical ideas by casting appropriate tradeoffs and comparisons among the methods of interest and by highlighting applications to decentralized training of machine learning models.