A near-optimal stochastic gradient method for decentralized non-convex finite-sum optimization
Paper and Code
Sep 15, 2020
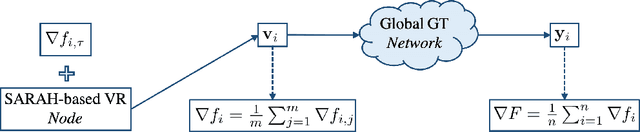
This paper describes a $near$-$optimal$ stochastic first-order gradient method for decentralized finite-sum minimization of smooth non-convex functions. Specifically, we propose GT-SARAH that employs a local SARAH-type variance reduction and global gradient tracking to address the stochastic and decentralized nature of the problem. Considering a total number of $N$ cost functions, equally divided over a directed network of $n$ nodes, we show that GT-SARAH finds an $\epsilon$-accurate first-order stationary point in ${\mathcal{O}(N^{1/2}\epsilon^{-1})}$ gradient computations across all nodes, independent of the network topology, when ${n\leq\mathcal{O}(N^{1/2}(1-\lambda)^{3})}$, where ${(1-\lambda)}$ is the spectral gap of the network weight matrix. In this regime, GT-SARAH is thus, to the best our knowledge, the first decentralized method that achieves the algorithmic lower bound for this class of problems. Moreover, GT-SARAH achieves a $non$-$asymptotic$ $linear$ $speedup$, in that, the total number of gradient computations at each node is reduced by a factor of $1/n$ compared to the near-optimal algorithms for this problem class that process all data at a single node. We also establish the convergence rate of GT-SARAH in other regimes, in terms of the relative sizes of the number of nodes $n$, total number of functions $N$, and the network spectral gap $(1-\lambda)$. Over infinite time horizon, we establish the almost sure and mean-squared convergence of GT-SARAH to a first-order stationary point.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge