Usman A. Khan
Multi-robot Path Planning and Scheduling via Model Predictive Optimal Transport (MPC-OT)
Aug 28, 2025Abstract:In this paper, we propose a novel methodology for path planning and scheduling for multi-robot navigation that is based on optimal transport theory and model predictive control. We consider a setup where $N$ robots are tasked to navigate to $M$ targets in a common space with obstacles. Mapping robots to targets first and then planning paths can result in overlapping paths that lead to deadlocks. We derive a strategy based on optimal transport that not only provides minimum cost paths from robots to targets but also guarantees non-overlapping trajectories. We achieve this by discretizing the space of interest into $K$ cells and by imposing a ${K\times K}$ cost structure that describes the cost of transitioning from one cell to another. Optimal transport then provides \textit{optimal and non-overlapping} cell transitions for the robots to reach the targets that can be readily deployed without any scheduling considerations. The proposed solution requires $\unicode{x1D4AA}(K^3\log K)$ computations in the worst-case and $\unicode{x1D4AA}(K^2\log K)$ for well-behaved problems. To further accommodate potentially overlapping trajectories (unavoidable in certain situations) as well as robot dynamics, we show that a temporal structure can be integrated into optimal transport with the help of \textit{replans} and \textit{model predictive control}.
DeepFleet: Multi-Agent Foundation Models for Mobile Robots
Aug 12, 2025
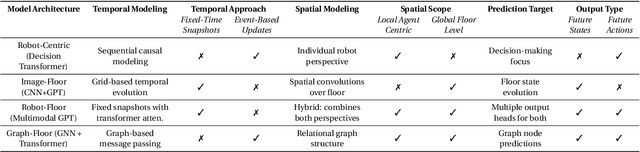
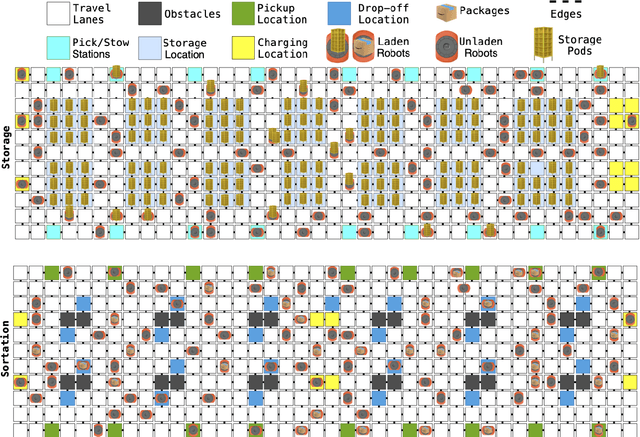
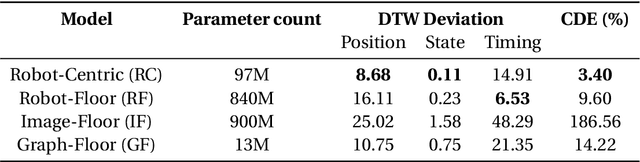
Abstract:We introduce DeepFleet, a suite of foundation models designed to support coordination and planning for large-scale mobile robot fleets. These models are trained on fleet movement data, including robot positions, goals, and interactions, from hundreds of thousands of robots in Amazon warehouses worldwide. DeepFleet consists of four architectures that each embody a distinct inductive bias and collectively explore key points in the design space for multi-agent foundation models: the robot-centric (RC) model is an autoregressive decision transformer operating on neighborhoods of individual robots; the robot-floor (RF) model uses a transformer with cross-attention between robots and the warehouse floor; the image-floor (IF) model applies convolutional encoding to a multi-channel image representation of the full fleet; and the graph-floor (GF) model combines temporal attention with graph neural networks for spatial relationships. In this paper, we describe these models and present our evaluation of the impact of these design choices on prediction task performance. We find that the robot-centric and graph-floor models, which both use asynchronous robot state updates and incorporate the localized structure of robot interactions, show the most promise. We also present experiments that show that these two models can make effective use of larger warehouses operation datasets as the models are scaled up.
Log-Scale Quantization in Distributed First-Order Methods: Gradient-based Learning from Distributed Data
Jun 02, 2024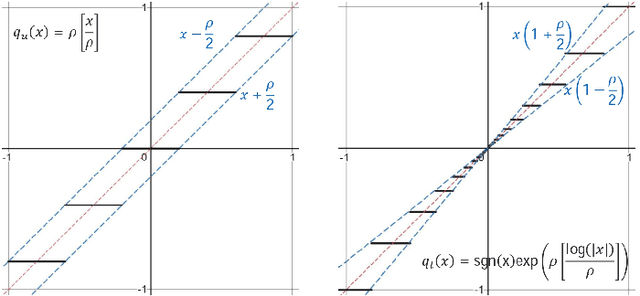
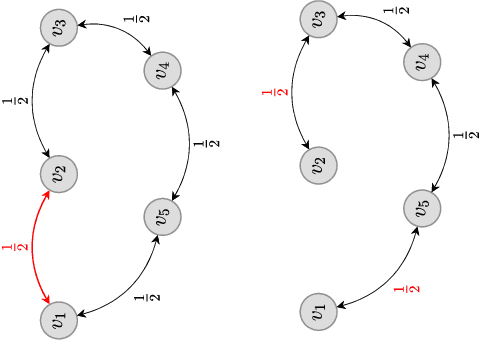
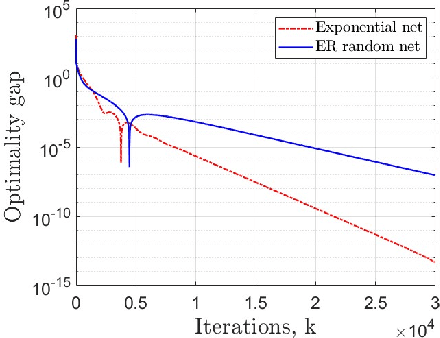
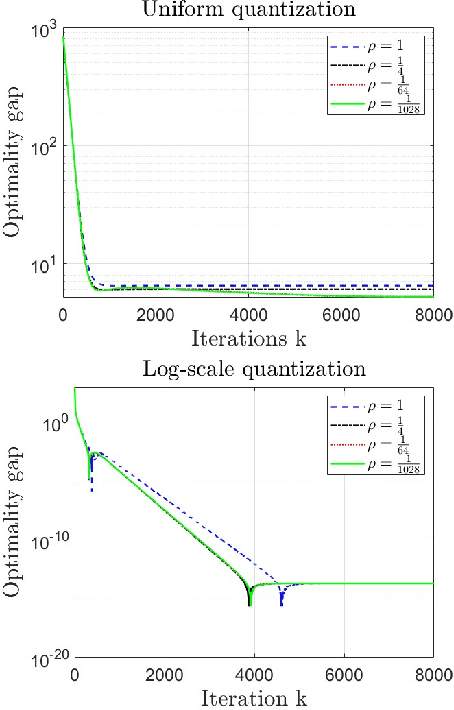
Abstract:Decentralized strategies are of interest for learning from large-scale data over networks. This paper studies learning over a network of geographically distributed nodes/agents subject to quantization. Each node possesses a private local cost function, collectively contributing to a global cost function, which the proposed methodology aims to minimize. In contrast to many existing literature, the information exchange among nodes is quantized. We adopt a first-order computationally-efficient distributed optimization algorithm (with no extra inner consensus loop) that leverages node-level gradient correction based on local data and network-level gradient aggregation only over nearby nodes. This method only requires balanced networks with no need for stochastic weight design. It can handle log-scale quantized data exchange over possibly time-varying and switching network setups. We analyze convergence over both structured networks (for example, training over data-centers) and ad-hoc multi-agent networks (for example, training over dynamic robotic networks). Through analysis and experimental validation, we show that (i) structured networks generally result in a smaller optimality gap, and (ii) logarithmic quantization leads to smaller optimality gap compared to uniform quantization.
Consensus-based Networked Tracking in Presence of Heterogeneous Time-Delays
Feb 15, 2023Abstract:We propose a distributed (single) target tracking scheme based on networked estimation and consensus algorithms over static sensor networks. The tracking part is based on linear time-difference-of-arrival (TDOA) measurement proposed in our previous works. This paper, in particular, develops delay-tolerant distributed filtering solutions over sparse data-transmission networks. We assume general arbitrary heterogeneous delays at different links. This may occur in many realistic large-scale applications where the data-sharing between different nodes is subject to latency due to communication-resource constraints or large spatially distributed sensor networks. The solution we propose in this work shows improved performance (verified by both theory and simulations) in such scenarios. Another privilege of such distributed schemes is the possibility to add localized fault-detection and isolation (FDI) strategies along with survivable graph-theoretic design, which opens many follow-up venues to this research. To our best knowledge no such delay-tolerant distributed linear algorithm is given in the existing distributed tracking literature.
Distributed saddle point problems for strongly concave-convex functions
Feb 11, 2022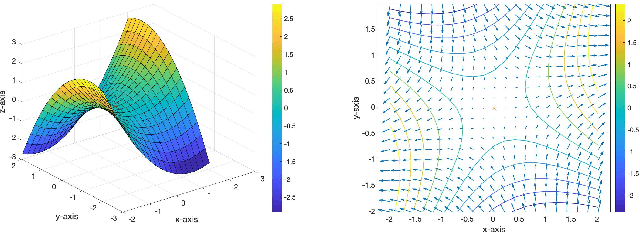
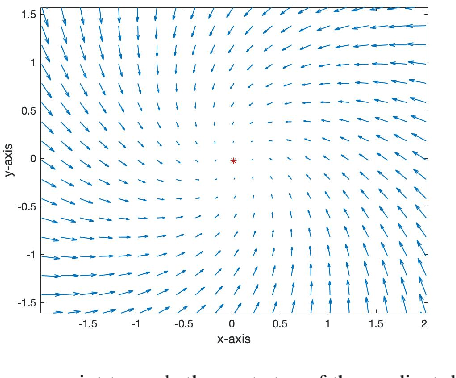
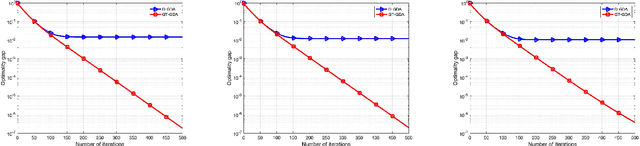
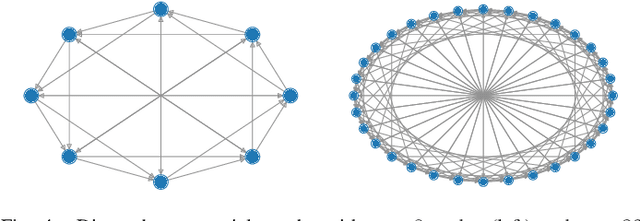
Abstract:In this paper, we propose GT-GDA, a distributed optimization method to solve saddle point problems of the form: $\min_{\mathbf{x}} \max_{\mathbf{y}} \{F(\mathbf{x},\mathbf{y}) :=G(\mathbf{x}) + \langle \mathbf{y}, \overline{P} \mathbf{x} \rangle - H(\mathbf{y})\}$, where the functions $G(\cdot)$, $H(\cdot)$, and the the coupling matrix $\overline{P}$ are distributed over a strongly connected network of nodes. GT-GDA is a first-order method that uses gradient tracking to eliminate the dissimilarity caused by heterogeneous data distribution among the nodes. In the most general form, GT-GDA includes a consensus over the local coupling matrices to achieve the optimal (unique) saddle point, however, at the expense of increased communication. To avoid this, we propose a more efficient variant GT-GDA-Lite that does not incur the additional communication and analyze its convergence in various scenarios. We show that GT-GDA converges linearly to the unique saddle point solution when $G(\cdot)$ is smooth and convex, $H(\cdot)$ is smooth and strongly convex, and the global coupling matrix $\overline{P}$ has full column rank. We further characterize the regime under which GT-GDA exhibits a network topology-independent convergence behavior. We next show the linear convergence of GT-GDA to an error around the unique saddle point, which goes to zero when the coupling cost ${\langle \mathbf y, \overline{P} \mathbf x \rangle}$ is common to all nodes, or when $G(\cdot)$ and $H(\cdot)$ are quadratic. Numerical experiments illustrate the convergence properties and importance of GT-GDA and GT-GDA-Lite for several applications.
Variance reduced stochastic optimization over directed graphs with row and column stochastic weights
Feb 07, 2022Abstract:This paper proposes AB-SAGA, a first-order distributed stochastic optimization method to minimize a finite-sum of smooth and strongly convex functions distributed over an arbitrary directed graph. AB-SAGA removes the uncertainty caused by the stochastic gradients using a node-level variance reduction and subsequently employs network-level gradient tracking to address the data dissimilarity across the nodes. Unlike existing methods that use the nonlinear push-sum correction to cancel the imbalance caused by the directed communication, the consensus updates in AB-SAGA are linear and uses both row and column stochastic weights. We show that for a constant step-size, AB-SAGA converges linearly to the global optimal. We quantify the directed nature of the underlying graph using an explicit directivity constant and characterize the regimes in which AB-SAGA achieves a linear speed-up over its centralized counterpart. Numerical experiments illustrate the convergence of AB-SAGA for strongly convex and nonconvex problems.
Distributed Detection and Mitigation of Biasing Attacks over Multi-Agent Networks
Sep 20, 2021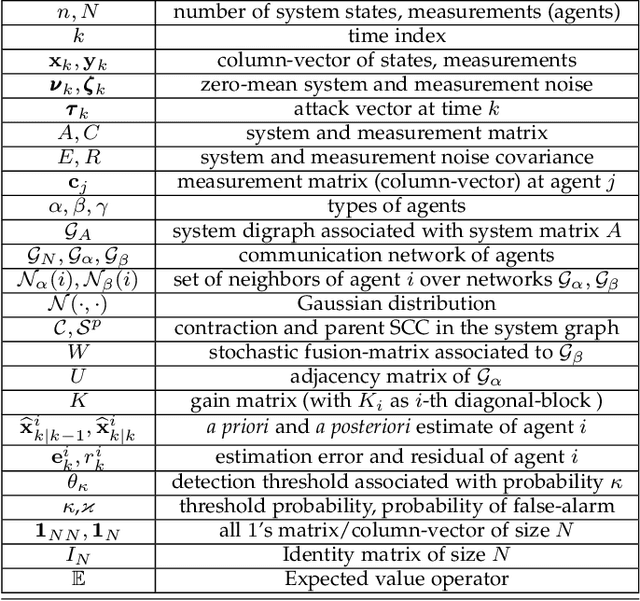
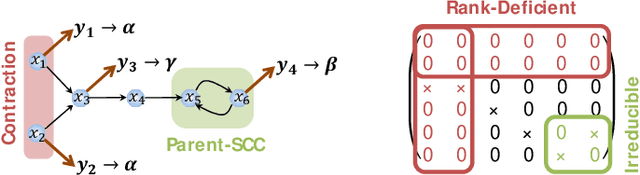
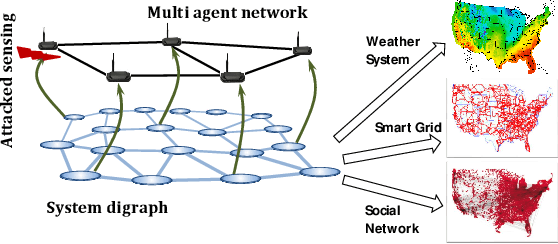
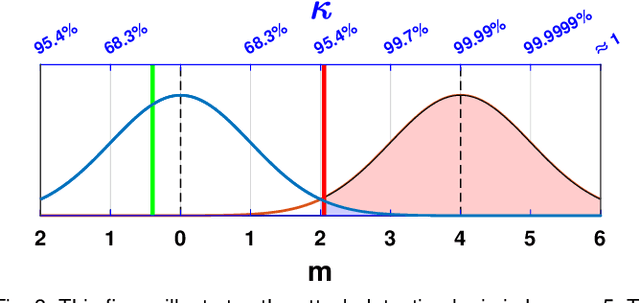
Abstract:This paper proposes a distributed attack detection and mitigation technique based on distributed estimation over a multi-agent network, where the agents take partial system measurements susceptible to (possible) biasing attacks. In particular, we assume that the system is not locally observable via the measurements in the direct neighborhood of any agent. First, for performance analysis in the attack-free case, we show that the proposed distributed estimation is unbiased with bounded mean-square deviation in steady-state. Then, we propose a residual-based strategy to locally detect possible attacks at agents. In contrast to the deterministic thresholds in the literature assuming an upper bound on the noise support, we define the thresholds on the residuals in a probabilistic sense. After detecting and isolating the attacked agent, a system-digraph-based mitigation strategy is proposed to replace the attacked measurement with a new observationally-equivalent one to recover potential observability loss. We adopt a graph-theoretic method to classify the agents based on their measurements, to distinguish between the agents recovering the system rank-deficiency and the ones recovering output-connectivity of the system digraph. The attack detection/mitigation strategy is specifically described for each type, which is of polynomial-order complexity for large-scale applications. Illustrative simulations support our theoretical results.
Distributed support-vector-machine over dynamic balanced directed networks
Apr 01, 2021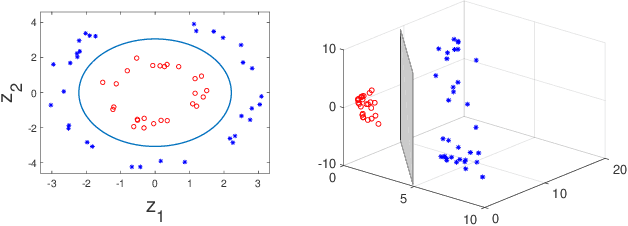
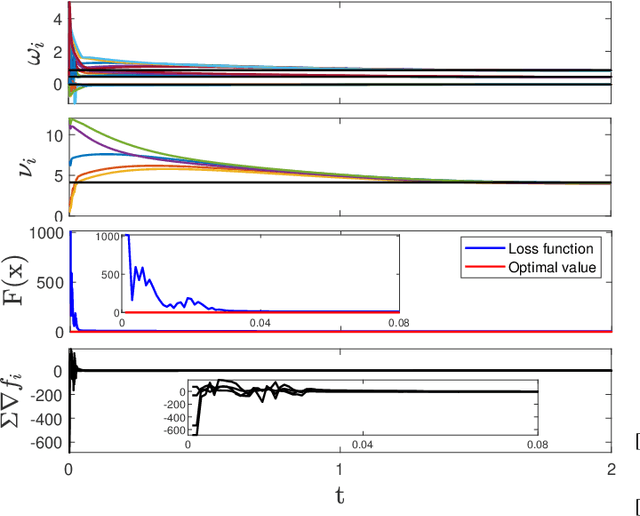
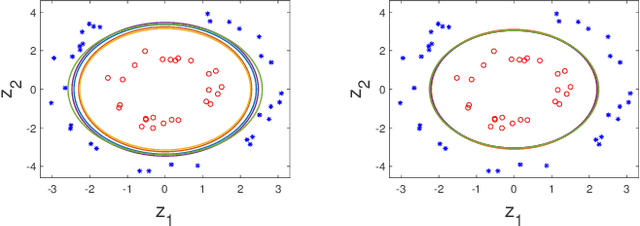
Abstract:In this paper, we consider the binary classification problem via distributed Support-Vector-Machines (SVM), where the idea is to train a network of agents, with limited share of data, to cooperatively learn the SVM classifier for the global database. Agents only share processed information regarding the classifier parameters and the gradient of the local loss functions instead of their raw data. In contrast to the existing work, we propose a continuous-time algorithm that incorporates network topology changes in discrete jumps. This hybrid nature allows us to remove chattering that arises because of the discretization of the underlying CT process. We show that the proposed algorithm converges to the SVM classifier over time-varying weight balanced directed graphs by using arguments from the matrix perturbation theory.
Delay-Tolerant Consensus-based Distributed Estimation: Full-Rank Systems with Potentially Unstable Dynamics
Apr 01, 2021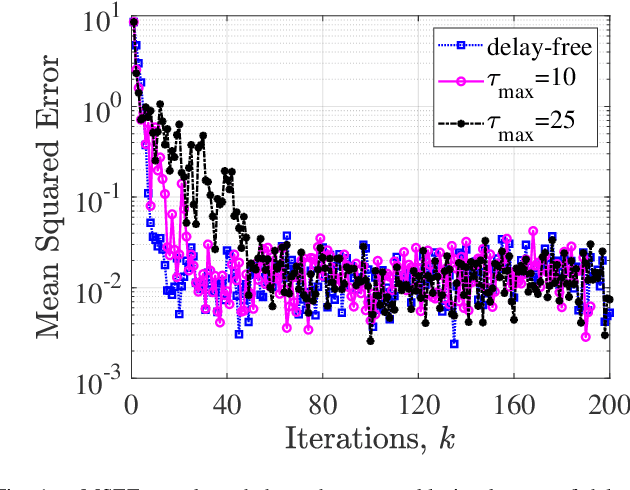
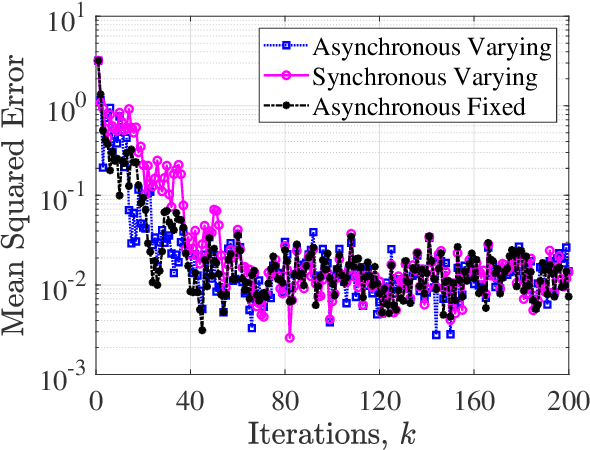
Abstract:Classical distributed estimation scenarios typically assume timely and reliable exchange of information over the multi-agent network. This paper, in contrast, considers single time-scale distributed estimation of (potentially) unstable full-rank dynamical systems via a multi-agent network subject to transmission time-delays. The proposed networked estimator consists of two steps: (i) consensus on (delayed) a-priori estimates, and (ii) measurement update. The agents only share their a-priori estimates with their in-neighbors over time-delayed transmission links. Considering the most general case, the delays are assumed to be time-varying, arbitrary, unknown, but upper-bounded. In contrast to most recent distributed observers assuming system observability in the neighborhood of each agent, our proposed estimator makes no such assumption. This may significantly reduce the communication/sensing loads on agents in large-scale, while making the (distributed) observability analysis more challenging. Using the notions of augmented matrices and Kronecker product, the geometric convergence of the proposed estimator over strongly-connected networks is proved irrespective of the bound on the time-delay. Simulations are provided to support our theoretical results.
A hybrid variance-reduced method for decentralized stochastic non-convex optimization
Feb 12, 2021
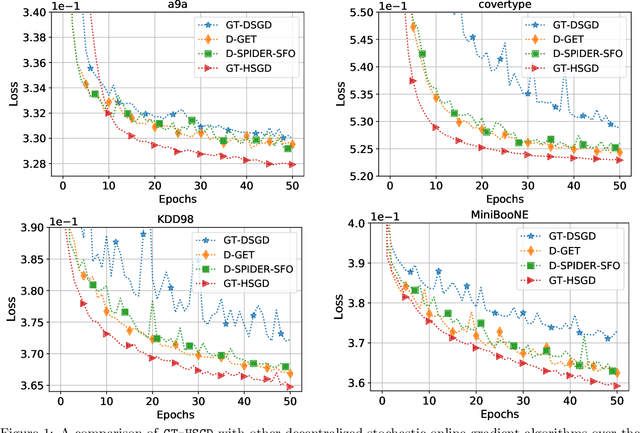
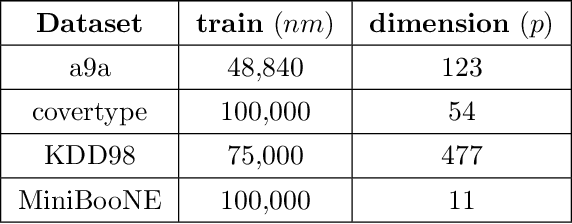
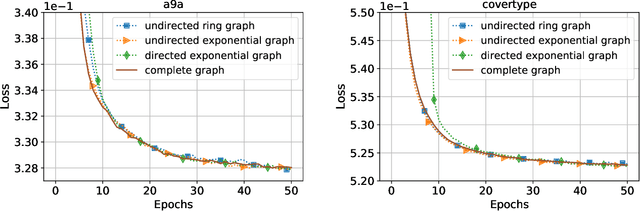
Abstract:This paper considers decentralized stochastic optimization over a network of~$n$ nodes, where each node possesses a smooth non-convex local cost function and the goal of the networked nodes is to find an~$\epsilon$-accurate first-order stationary point of the sum of the local costs. We focus on an online setting, where each node accesses its local cost only by means of a stochastic first-order oracle that returns a noisy version of the exact gradient. In this context, we propose a novel single-loop decentralized hybrid variance-reduced stochastic gradient method, called \texttt{GT-HSGD}, that outperforms the existing approaches in terms of both the oracle complexity and practical implementation. The \texttt{GT-HSGD} algorithm implements specialized local hybrid stochastic gradient estimators that are fused over the network to track the global gradient. Remarkably, \texttt{GT-HSGD} achieves a network-independent oracle complexity of~$O(n^{-1}\epsilon^{-3})$ when the required error tolerance~$\epsilon$ is small enough, leading to a linear speedup with respect to the centralized optimal online variance-reduced approaches that operate on a single node. Numerical experiments are provided to illustrate our main technical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge