Survey of Distributed Algorithms for Resource Allocation over Multi-Agent Systems

Resource allocation and scheduling in multi-agent systems present challenges due to complex interactions and decentralization. This survey paper provides a comprehensive analysis of distributed algorithms for addressing the distributed resource allocation (DRA) problem over multi-agent systems. It covers a significant area of research at the intersection of optimization, multi-agent systems, and distributed consensus-based computing. The paper begins by presenting a mathematical formulation of the DRA problem, establishing a solid foundation for further exploration. Real-world applications of DRA in various domains are examined to underscore the importance of efficient resource allocation, and relevant distributed optimization formulations are presented. The survey then delves into existing solutions for DRA, encompassing linear, nonlinear, primal-based, and dual-formulation-based approaches. Furthermore, this paper evaluates the features and properties of DRA algorithms, addressing key aspects such as feasibility, convergence rate, and network reliability. The analysis of mathematical foundations, diverse applications, existing solutions, and algorithmic properties contributes to a broader comprehension of the challenges and potential solutions for this domain.

Discretized Distributed Optimization over Dynamic Digraphs

We consider a discrete-time model of continuous-time distributed optimization over dynamic directed-graphs (digraphs) with applications to distributed learning. Our optimization algorithm works over general strongly connected dynamic networks under switching topologies, e.g., in mobile multi-agent systems and volatile networks due to link failures. Compared to many existing lines of work, there is no need for bi-stochastic weight designs on the links. The existing literature mostly needs the link weights to be stochastic using specific weight-design algorithms needed both at the initialization and at all times when the topology of the network changes. This paper eliminates the need for such algorithms and paves the way for distributed optimization over time-varying digraphs. We derive the bound on the gradient-tracking step-size and discrete time-step for convergence and prove dynamic stability using arguments from consensus algorithms, matrix perturbation theory, and Lyapunov theory. This work, particularly, is an improvement over existing stochastic-weight undirected networks in case of link removal or packet drops. This is because the existing literature may need to rerun time-consuming and computationally complex algorithms for stochastic design, while the proposed strategy works as long as the underlying network is weight-symmetric and balanced. The proposed optimization framework finds applications to distributed classification and learning.

D-SVM over Networked Systems with Non-Ideal Linking Conditions

This paper considers distributed optimization algorithms, with application in binary classification via distributed support-vector-machines (D-SVM) over multi-agent networks subject to some link nonlinearities. The agents solve a consensus-constraint distributed optimization cooperatively via continuous-time dynamics, while the links are subject to strongly sign-preserving odd nonlinear conditions. Logarithmic quantization and clipping (saturation) are two examples of such nonlinearities. In contrast to existing literature that mostly considers ideal links and perfect information exchange over linear channels, we show how general sector-bounded models affect the convergence to the optimizer (i.e., the SVM classifier) over dynamic balanced directed networks. In general, any odd sector-bounded nonlinear mapping can be applied to our dynamics. The main challenge is to show that the proposed system dynamics always have one zero eigenvalue (associated with the consensus) and the other eigenvalues all have negative real parts. This is done by recalling arguments from matrix perturbation theory. Then, the solution is shown to converge to the agreement state under certain conditions. For example, the gradient tracking (GT) step size is tighter than the linear case by factors related to the upper/lower sector bounds. To the best of our knowledge, no existing work in distributed optimization and learning literature considers non-ideal link conditions.

Distributed Detection and Mitigation of Biasing Attacks over Multi-Agent Networks

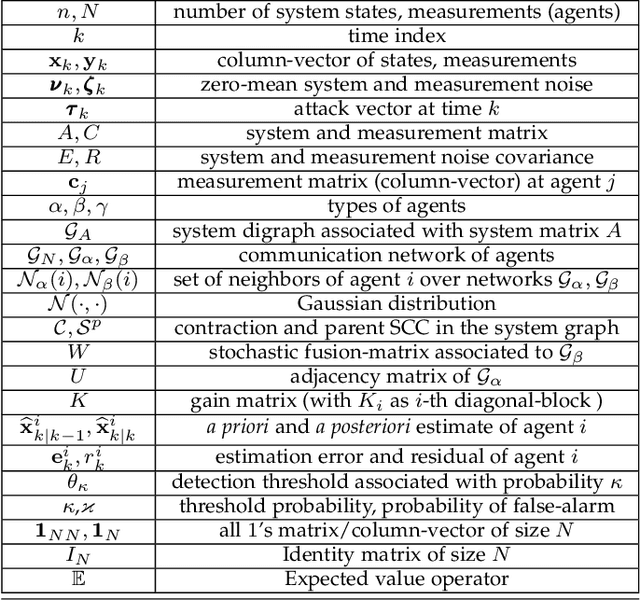
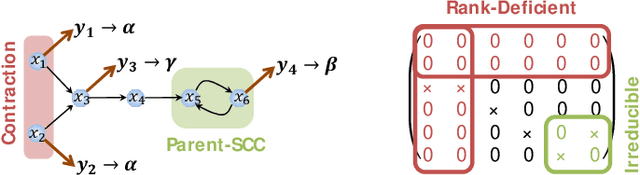
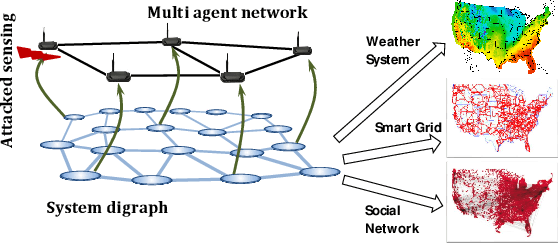
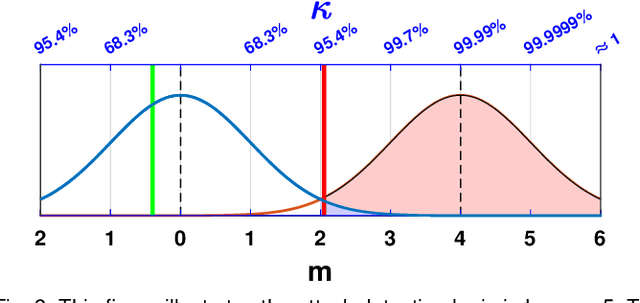
This paper proposes a distributed attack detection and mitigation technique based on distributed estimation over a multi-agent network, where the agents take partial system measurements susceptible to (possible) biasing attacks. In particular, we assume that the system is not locally observable via the measurements in the direct neighborhood of any agent. First, for performance analysis in the attack-free case, we show that the proposed distributed estimation is unbiased with bounded mean-square deviation in steady-state. Then, we propose a residual-based strategy to locally detect possible attacks at agents. In contrast to the deterministic thresholds in the literature assuming an upper bound on the noise support, we define the thresholds on the residuals in a probabilistic sense. After detecting and isolating the attacked agent, a system-digraph-based mitigation strategy is proposed to replace the attacked measurement with a new observationally-equivalent one to recover potential observability loss. We adopt a graph-theoretic method to classify the agents based on their measurements, to distinguish between the agents recovering the system rank-deficiency and the ones recovering output-connectivity of the system digraph. The attack detection/mitigation strategy is specifically described for each type, which is of polynomial-order complexity for large-scale applications. Illustrative simulations support our theoretical results.