On the Design of Resilient Distributed Single Time-Scale Estimators: A Graph-Theoretic Approach

Distributed estimation in interconnected systems has gained increasing attention due to its relevance in diverse applications such as sensor networks, autonomous vehicles, and cloud computing. In real practice, the sensor network may suffer from communication and/or sensor failures. This might be due to cyber-attacks, faults, or environmental conditions. Distributed estimation resilient to such conditions is the topic of this paper. By representing the sensor network as a graph and exploiting its inherent structural properties, we introduce novel techniques that enhance the robustness of distributed estimators. As compared to the literature, the proposed estimator (i) relaxes the network connectivity of most existing single time-scale estimators and (ii) reduces the communication load of the existing double time-scale estimators by avoiding the inner consensus loop. On the other hand, the sensors might be subject to faults or attacks, resulting in biased measurements. Removing these sensor data may result in observability loss. Therefore, we propose resilient design on the definitions of $q$-node-connectivity and $q$-link-connectivity, which capture robust strong-connectivity under link or sensor node failure. By proper design of the sensor network, we prove Schur stability of the proposed distributed estimation protocol under failure of up to $q$ sensors or $q$ communication links.

Momentum-based Distributed Resource Scheduling Optimization Subject to Sector-Bound Nonlinearity and Latency

This paper proposes an accelerated consensus-based distributed iterative algorithm for resource allocation and scheduling. The proposed gradient-tracking algorithm introduces an auxiliary variable to add momentum towards the optimal state. We prove that this solution is all-time feasible, implying that the coupling constraint always holds along the algorithm iterative procedure; therefore, the algorithm can be terminated at any time. This is in contrast to the ADMM-based solutions that meet constraint feasibility asymptotically. Further, we show that the proposed algorithm can handle possible link nonlinearity due to logarithmically-quantized data transmission (or any sign-preserving odd sector-bound nonlinear mapping). We prove convergence over uniformly-connected dynamic networks (i.e., a hybrid setup) that may occur in mobile and time-varying multi-agent networks. Further, the latency issue over the network is addressed by proposing delay-tolerant solutions. To our best knowledge, accelerated momentum-based convergence, nonlinear linking, all-time feasibility, uniform network connectivity, and handling (possible) time delays are not altogether addressed in the literature. These contributions make our solution practical in many real-world applications.

Fully Distributed and Quantized Algorithm for MPC-based Autonomous Vehicle Platooning Optimization

Intelligent transportation systems have recently emerged to address the growing interest for safer, more efficient, and sustainable transportation solutions. In this direction, this paper presents distributed algorithms for control and optimization over vehicular networks. First, we formulate the autonomous vehicle platooning framework based on model-predictive-control (MPC) strategies and present its objective optimization as a cooperative quadratic cost function. Then, we propose a distributed algorithm to locally optimize this objective at every vehicle subject to data quantization over the communication network of vehicles. In contrast to most existing literature that assumes ideal communication channels, log-scale data quantization over the network is addressed in this work, which is more realistic and practical. In particular, we show by simulation that the proposed log-quantized algorithm reaches optimal convergence with less residual and optimality gap. This outperforms the existing literature considering uniform quantization which leads to a large optimality gap and residual.

Distributed Observer Design for Tracking Platoon of Connected and Autonomous Vehicles

Intelligent transportation systems (ITS) aim to advance innovative strategies relating to different modes of transport, traffic management, and autonomous vehicles. This paper studies the platoon of connected and autonomous vehicles (CAV) and proposes a distributed observer to track the state of the CAV dynamics. First, we model the CAV dynamics via an LTI interconnected system. Then, a consensus-based strategy is proposed to infer the state of the CAV dynamics based on local information exchange over the communication network of vehicles. A linear-matrix-inequality (LMI) technique is adopted for the block-diagonal observer gain design such that this gain is associated in a distributed way and locally to every vehicle. The distributed observer error dynamics is then shown to follow the structure of the Kronecker matrix product of the system dynamics and the adjacency matrix of the CAV network. The notions of survivable network design and redundant observer scheme are further discussed in the paper to address resilience to link and node failure. Finally, we verify our theoretical contributions via numerical simulations.

Distributed Target Tracking based on Localization with Linear Time-Difference-of-Arrival Measurements: A Delay-Tolerant Networked Estimation Approach

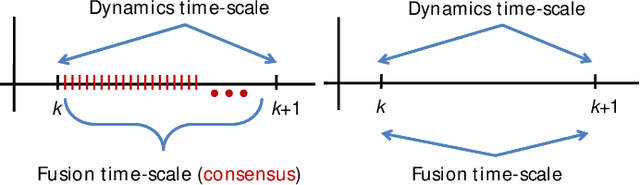
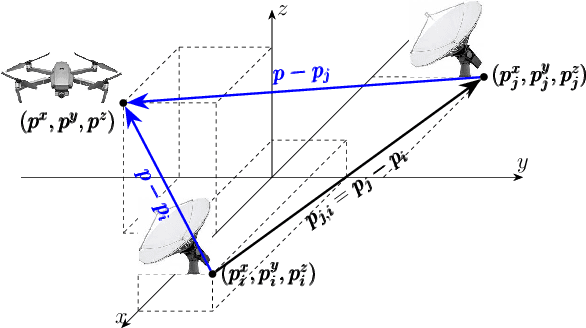
This paper considers target tracking based on a beacon signal's time-difference-of-arrival (TDOA) to a group of cooperating sensors. The sensors receive a reflected signal from the target where the time-of-arrival (TOA) renders the distance information. The existing approaches include: (i) classic centralized solutions which gather and process the target data at a central unit, (ii) distributed solutions which assume that the target data is observable in the dense neighborhood of each sensor (to be filtered locally), and (iii) double time-scale distributed methods with high rates of communication/consensus over the network. This work, in order to reduce the network connectivity in (i)-(ii) and communication rate in (iii), proposes a distributed single time-scale technique, which can also handle heterogeneous constant data-exchange delays over the static sensor network. This work assumes only distributed observability (in contrast to local observability in some existing works categorized in (ii)), i.e., the target is observable globally over a (strongly) connected network. The (strong) connectivity further allows for survivable network and $q$-redundant observer design. Each sensor locally shares information and processes the received data in its immediate neighborhood via local linear-matrix-inequalities (LMI) feedback gains to ensure tracking error stability. The same gain matrix works in the presence of heterogeneous delays with no need of redesigning algorithms. Since most existing distributed estimation scenarios are linear (based on consensus), many works use linearization of the existing nonlinear TDOA measurement models where the output matrix is a function of the target position.

Decentralized Mobile Target Tracking Using Consensus-Based Estimation with Nearly-Constant-Velocity Modeling

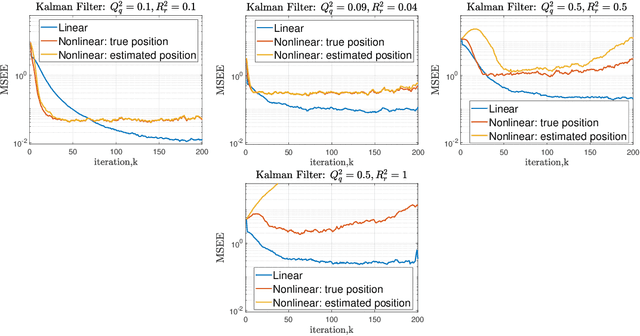
Mobile target tracking is crucial in various applications such as surveillance and autonomous navigation. This study presents a decentralized tracking framework utilizing a Consensus-Based Estimation Filter (CBEF) integrated with the Nearly-Constant-Velocity (NCV) model to predict a moving target's state. The framework facilitates agents in a network to collaboratively estimate the target's position by sharing local observations and achieving consensus despite communication constraints and measurement noise. A saturation-based filtering technique is employed to enhance robustness by mitigating the impact of noisy sensor data. Simulation results demonstrate that the proposed method effectively reduces the Mean Squared Estimation Error (MSEE) over time, indicating improved estimation accuracy and reliability. The findings underscore the effectiveness of the CBEF in decentralized environments, highlighting its scalability and resilience in the presence of uncertainties.

Logarithmically Quantized Distributed Optimization over Dynamic Multi-Agent Networks

Distributed optimization finds many applications in machine learning, signal processing, and control systems. In these real-world applications, the constraints of communication networks, particularly limited bandwidth, necessitate implementing quantization techniques. In this paper, we propose distributed optimization dynamics over multi-agent networks subject to logarithmically quantized data transmission. Under this condition, data exchange benefits from representing smaller values with more bits and larger values with fewer bits. As compared to uniform quantization, this allows for higher precision in representing near-optimal values and more accuracy of the distributed optimization algorithm. The proposed optimization dynamics comprise a primary state variable converging to the optimizer and an auxiliary variable tracking the objective function's gradient. Our setting accommodates dynamic network topologies, resulting in a hybrid system requiring convergence analysis using matrix perturbation theory and eigenspectrum analysis.

Nonlinear Perturbation-based Non-Convex Optimization over Time-Varying Networks

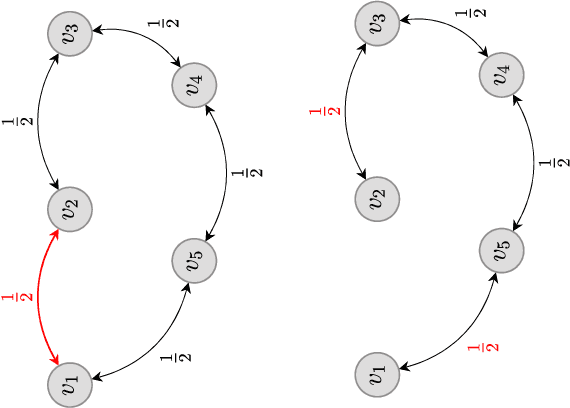
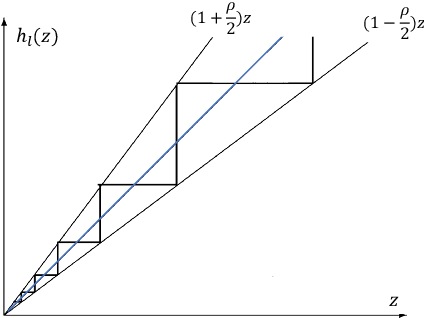
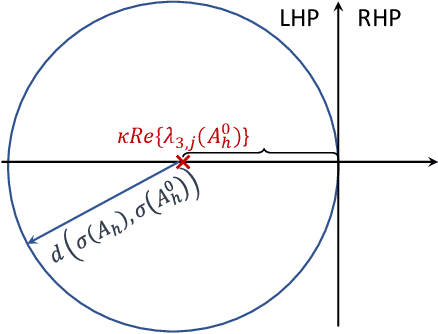
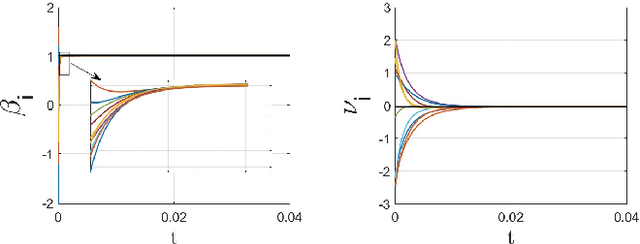
Decentralized optimization strategies are helpful for various applications, from networked estimation to distributed machine learning. This paper studies finite-sum minimization problems described over a network of nodes and proposes a computationally efficient algorithm that solves distributed convex problems and optimally finds the solution to locally non-convex objective functions. In contrast to batch gradient optimization in some literature, our algorithm is on a single-time scale with no extra inner consensus loop. It evaluates one gradient entry per node per time. Further, the algorithm addresses link-level nonlinearity representing, for example, logarithmic quantization of the exchanged data or clipping of the exchanged data bits. Leveraging perturbation-based theory and algebraic Laplacian network analysis proves optimal convergence and dynamics stability over time-varying and switching networks. The time-varying network setup might be due to packet drops or link failures. Despite the nonlinear nature of the dynamics, we prove exact convergence in the face of odd sign-preserving sector-bound nonlinear data transmission over the links. Illustrative numerical simulations further highlight our contributions.

Log-Scale Quantization in Distributed First-Order Methods: Gradient-based Learning from Distributed Data

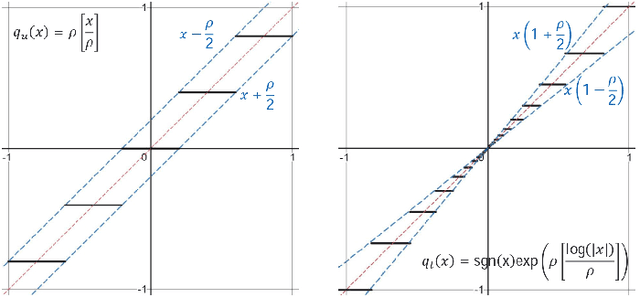
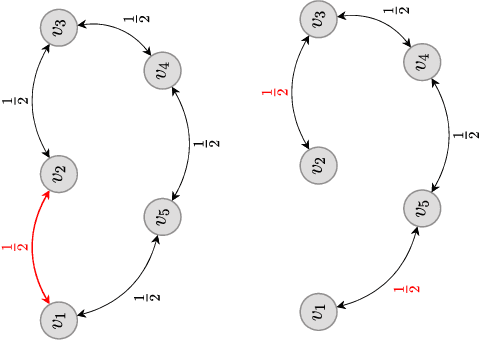
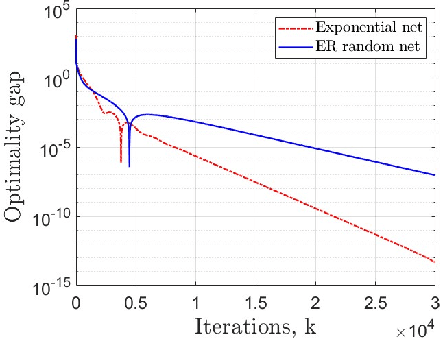
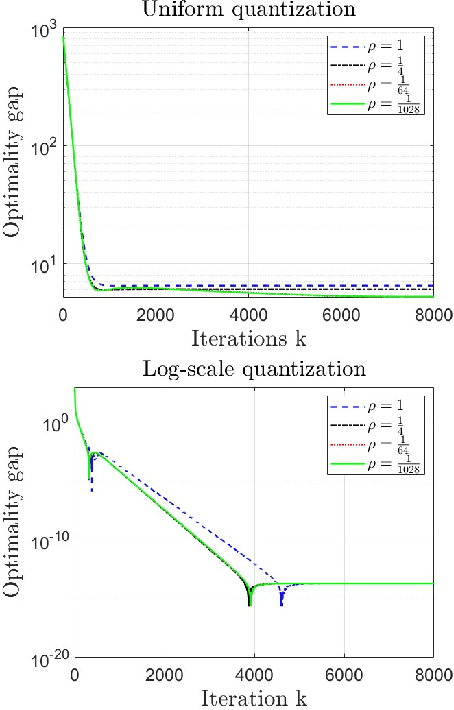
Decentralized strategies are of interest for learning from large-scale data over networks. This paper studies learning over a network of geographically distributed nodes/agents subject to quantization. Each node possesses a private local cost function, collectively contributing to a global cost function, which the proposed methodology aims to minimize. In contrast to many existing literature, the information exchange among nodes is quantized. We adopt a first-order computationally-efficient distributed optimization algorithm (with no extra inner consensus loop) that leverages node-level gradient correction based on local data and network-level gradient aggregation only over nearby nodes. This method only requires balanced networks with no need for stochastic weight design. It can handle log-scale quantized data exchange over possibly time-varying and switching network setups. We analyze convergence over both structured networks (for example, training over data-centers) and ad-hoc multi-agent networks (for example, training over dynamic robotic networks). Through analysis and experimental validation, we show that (i) structured networks generally result in a smaller optimality gap, and (ii) logarithmic quantization leads to smaller optimality gap compared to uniform quantization.

Accelerated Distributed Allocation

Distributed allocation finds applications in many scenarios including CPU scheduling, distributed energy resource management, and networked coverage control. In this paper, we propose a fast convergent optimization algorithm with a tunable rate using the signum function. The convergence rate of the proposed algorithm can be managed by changing two parameters. We prove convergence over uniformly-connected multi-agent networks. Therefore, the solution converges even if the network loses connectivity at some finite time intervals. The proposed algorithm is all-time feasible, implying that at any termination time of the algorithm, the resource-demand feasibility holds. This is in contrast to asymptotic feasibility in many dual formulation solutions (e.g., ADMM) that meet resource-demand feasibility over time and asymptotically.