Log-Scale Quantization in Distributed First-Order Methods: Gradient-based Learning from Distributed Data

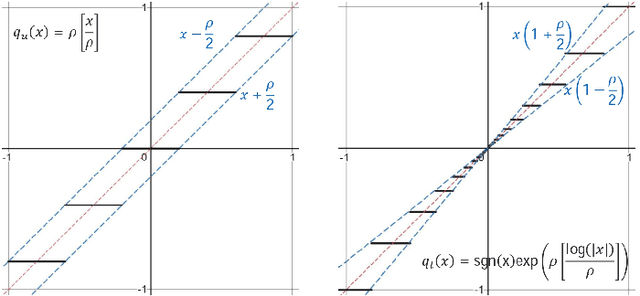
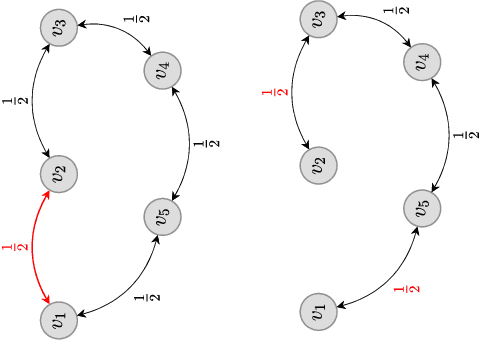
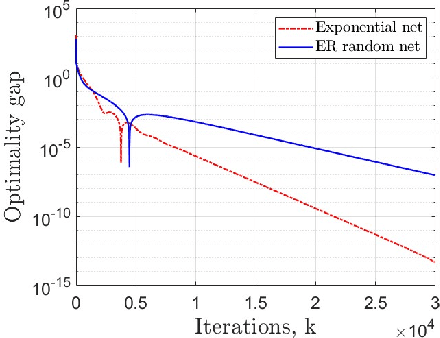
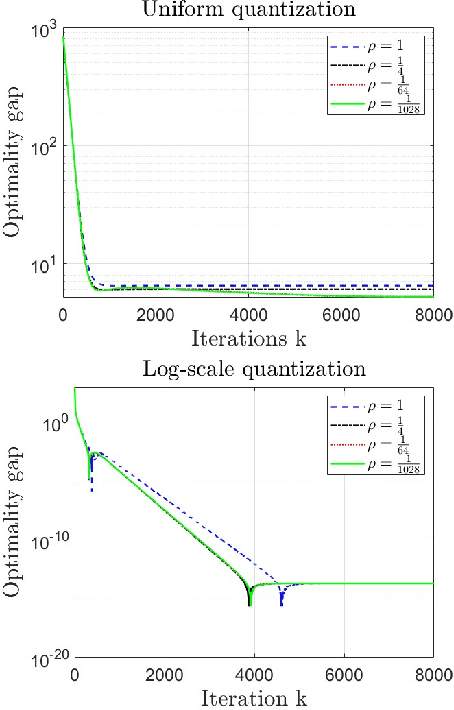
Decentralized strategies are of interest for learning from large-scale data over networks. This paper studies learning over a network of geographically distributed nodes/agents subject to quantization. Each node possesses a private local cost function, collectively contributing to a global cost function, which the proposed methodology aims to minimize. In contrast to many existing literature, the information exchange among nodes is quantized. We adopt a first-order computationally-efficient distributed optimization algorithm (with no extra inner consensus loop) that leverages node-level gradient correction based on local data and network-level gradient aggregation only over nearby nodes. This method only requires balanced networks with no need for stochastic weight design. It can handle log-scale quantized data exchange over possibly time-varying and switching network setups. We analyze convergence over both structured networks (for example, training over data-centers) and ad-hoc multi-agent networks (for example, training over dynamic robotic networks). Through analysis and experimental validation, we show that (i) structured networks generally result in a smaller optimality gap, and (ii) logarithmic quantization leads to smaller optimality gap compared to uniform quantization.

Distributed saddle point problems for strongly concave-convex functions

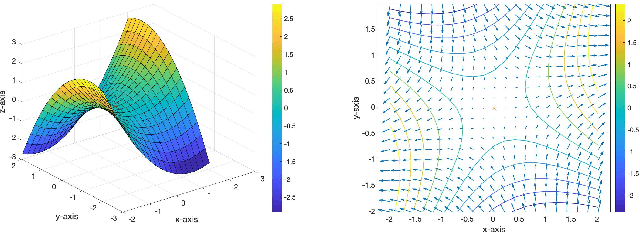
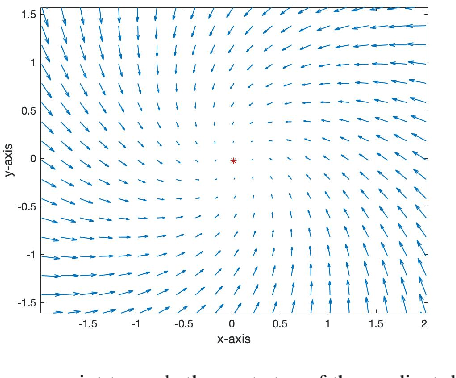
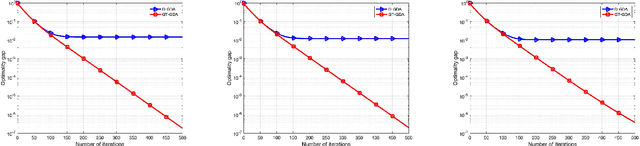
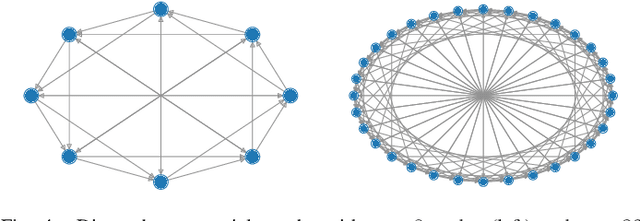
In this paper, we propose GT-GDA, a distributed optimization method to solve saddle point problems of the form: $\min_{\mathbf{x}} \max_{\mathbf{y}} \{F(\mathbf{x},\mathbf{y}) :=G(\mathbf{x}) + \langle \mathbf{y}, \overline{P} \mathbf{x} \rangle - H(\mathbf{y})\}$, where the functions $G(\cdot)$, $H(\cdot)$, and the the coupling matrix $\overline{P}$ are distributed over a strongly connected network of nodes. GT-GDA is a first-order method that uses gradient tracking to eliminate the dissimilarity caused by heterogeneous data distribution among the nodes. In the most general form, GT-GDA includes a consensus over the local coupling matrices to achieve the optimal (unique) saddle point, however, at the expense of increased communication. To avoid this, we propose a more efficient variant GT-GDA-Lite that does not incur the additional communication and analyze its convergence in various scenarios. We show that GT-GDA converges linearly to the unique saddle point solution when $G(\cdot)$ is smooth and convex, $H(\cdot)$ is smooth and strongly convex, and the global coupling matrix $\overline{P}$ has full column rank. We further characterize the regime under which GT-GDA exhibits a network topology-independent convergence behavior. We next show the linear convergence of GT-GDA to an error around the unique saddle point, which goes to zero when the coupling cost ${\langle \mathbf y, \overline{P} \mathbf x \rangle}$ is common to all nodes, or when $G(\cdot)$ and $H(\cdot)$ are quadratic. Numerical experiments illustrate the convergence properties and importance of GT-GDA and GT-GDA-Lite for several applications.

Variance reduced stochastic optimization over directed graphs with row and column stochastic weights

This paper proposes AB-SAGA, a first-order distributed stochastic optimization method to minimize a finite-sum of smooth and strongly convex functions distributed over an arbitrary directed graph. AB-SAGA removes the uncertainty caused by the stochastic gradients using a node-level variance reduction and subsequently employs network-level gradient tracking to address the data dissimilarity across the nodes. Unlike existing methods that use the nonlinear push-sum correction to cancel the imbalance caused by the directed communication, the consensus updates in AB-SAGA are linear and uses both row and column stochastic weights. We show that for a constant step-size, AB-SAGA converges linearly to the global optimal. We quantify the directed nature of the underlying graph using an explicit directivity constant and characterize the regimes in which AB-SAGA achieves a linear speed-up over its centralized counterpart. Numerical experiments illustrate the convergence of AB-SAGA for strongly convex and nonconvex problems.

Push-SAGA: A decentralized stochastic algorithm with variance reduction over directed graphs

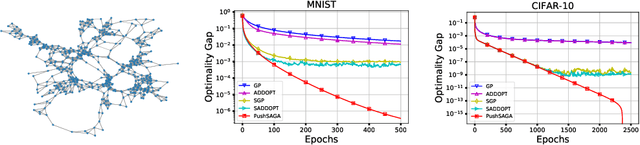
In this paper, we propose Push-SAGA, a decentralized stochastic first-order method for finite-sum minimization over a directed network of nodes. Push-SAGA combines node-level variance reduction to remove the uncertainty caused by stochastic gradients, network-level gradient tracking to address the distributed nature of the data, and push-sum consensus to tackle the challenge of directed communication links. We show that Push-SAGA achieves linear convergence to the exact solution for smooth and strongly convex problems and is thus the first linearly-convergent stochastic algorithm over arbitrary strongly connected directed graphs. We also characterize the regimes in which Push-SAGA achieves a linear speed-up compared to its centralized counterpart and achieves a network-independent convergence rate. We illustrate the behavior and convergence properties of Push-SAGA with the help of numerical experiments on strongly convex and non-convex problems.

S-ADDOPT: Decentralized stochastic first-order optimization over directed graphs

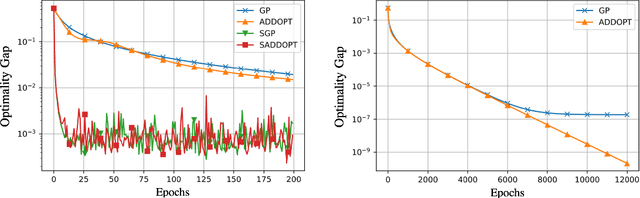
In this report, we study decentralized stochastic optimization to minimize a sum of smooth and strongly convex cost functions when the functions are distributed over a directed network of nodes. In contrast to the existing work, we use gradient tracking to improve certain aspects of the resulting algorithm. In particular, we propose the S-ADDOPT algorithm that assumes a stochastic first-order oracle at each node and show that for a constant step-size $\alpha$, each node converges linearly inside an error ball around the optimal solution, the size of which is controlled by $\alpha$. For decaying step-sizes $\mathcal{O}(1/k)$, we show that S-ADDOPT reaches the exact solution sublinearly at $\mathcal{O}(1/k)$ and its convergence is asymptotically network-independent. Thus the asymptotic behavior of S-ADDOPT is comparable to the centralized stochastic gradient descent. Numerical experiments over both strongly convex and non-convex problems illustrate the convergence behavior and the performance comparison of the proposed algorithm.