Distributed Gradient Clustering: Convergence and the Effect of Initialization

We study the effects of center initialization on the performance of a family of distributed gradient-based clustering algorithms introduced in [1], that work over connected networks of users. In the considered scenario, each user contains a local dataset and communicates only with its immediate neighbours, with the aim of finding a global clustering of the joint data. We perform extensive numerical experiments, evaluating the effects of center initialization on the performance of our family of methods, demonstrating that our methods are more resilient to the effects of initialization, compared to centralized gradient clustering [2]. Next, inspired by the $K$-means++ initialization [3], we propose a novel distributed center initialization scheme, which is shown to improve the performance of our methods, compared to the baseline random initialization.

Tight Long-Term Tail Decay of (Clipped) SGD in Non-Convex Optimization

The study of tail behaviour of SGD-induced processes has been attracting a lot of interest, due to offering strong guarantees with respect to individual runs of an algorithm. While many works provide high-probability guarantees, quantifying the error rate for a fixed probability threshold, there is a lack of work directly studying the probability of failure, i.e., quantifying the tail decay rate for a fixed error threshold. Moreover, existing results are of finite-time nature, limiting their ability to capture the true long-term tail decay which is more informative for modern learning models, typically trained for millions of iterations. Our work closes these gaps, by studying the long-term tail decay of SGD-based methods through the lens of large deviations theory, establishing several strong results in the process. First, we provide an upper bound on the tails of the gradient norm-squared of the best iterate produced by (vanilla) SGD, for non-convex costs and bounded noise, with long-term decay at rate $e^{-t/\log(t)}$. Next, we relax the noise assumption by considering clipped SGD (c-SGD) under heavy-tailed noise with bounded moment of order $p \in (1,2]$, showing an upper bound with long-term decay at rate $e^{-t^{β_p}/\log(t)}$, where $β_p = \frac{4(p-1)}{3p-2}$ for $p \in (1,2)$ and $e^{-t/\log^2(t)}$ for $p = 2$. Finally, we provide lower bounds on the tail decay, at rate $e^{-t}$, showing that our rates for both SGD and c-SGD are tight, up to poly-logarithmic factors. Notably, our results demonstrate an order of magnitude faster long-term tail decay compared to existing work based on finite-time bounds, which show rates $e^{-\sqrt{t}}$ and $e^{-t^{β_p/2}}$, $p \in (1,2]$, for SGD and c-SGD, respectively. As such, we uncover regimes where the tails decay much faster than previously known, providing stronger long-term guarantees for individual runs.

Test-Time Scaling in Diffusion LLMs via Hidden Semi-Autoregressive Experts

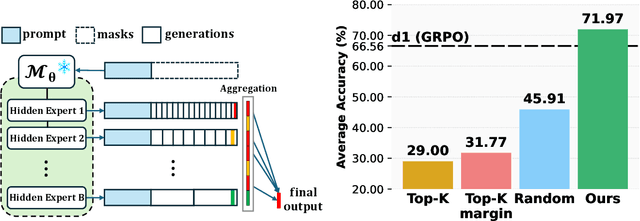
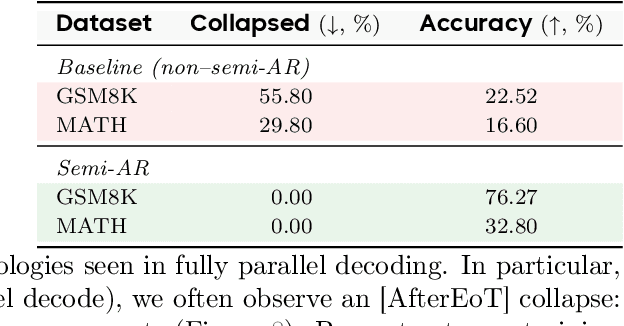
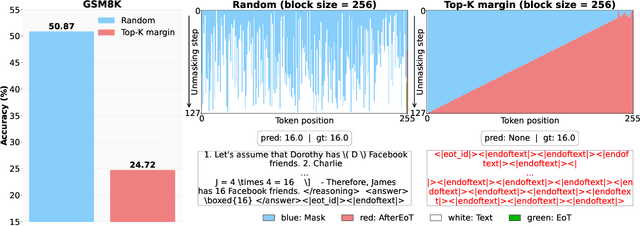
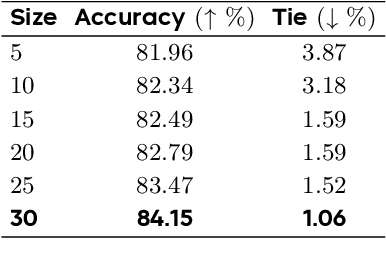
Diffusion-based large language models (dLLMs) are trained flexibly to model extreme dependence in the data distribution; however, how to best utilize this information at inference time remains an open problem. In this work, we uncover an interesting property of these models: dLLMs trained on textual data implicitly learn a mixture of semi-autoregressive experts, where different generation orders reveal different specialized behaviors. We show that committing to any single, fixed inference time schedule, a common practice, collapses performance by failing to leverage this latent ensemble. To address this, we introduce HEX (Hidden semiautoregressive EXperts for test-time scaling), a training-free inference method that ensembles across heterogeneous block schedules. By doing a majority vote over diverse block-sized generation paths, HEX robustly avoids failure modes associated with any single fixed schedule. On reasoning benchmarks such as GSM8K, it boosts accuracy by up to 3.56X (from 24.72% to 88.10%), outperforming top-K margin inference and specialized fine-tuned methods like GRPO, without additional training. HEX even yields significant gains on MATH benchmark from 16.40% to 40.00%, scientific reasoning on ARC-C from 54.18% to 87.80%, and TruthfulQA from 28.36% to 57.46%. Our results establish a new paradigm for test-time scaling in diffusion-based LLMs (dLLMs), revealing that the sequence in which masking is performed plays a critical role in determining performance during inference.

Federated Multi-Objective Learning with Controlled Pareto Frontiers

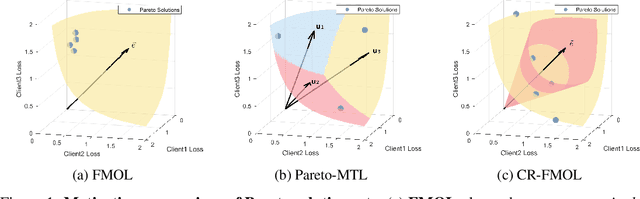
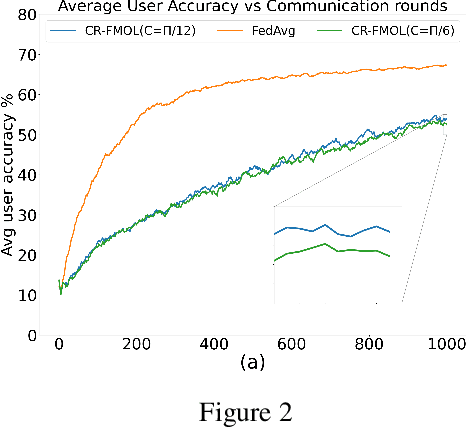
Federated learning (FL) is a widely adopted paradigm for privacy-preserving model training, but FedAvg optimise for the majority while under-serving minority clients. Existing methods such as federated multi-objective learning (FMOL) attempts to import multi-objective optimisation (MOO) into FL. However, it merely delivers task-wise Pareto-stationary points, leaving client fairness to chance. In this paper, we introduce Conically-Regularised FMOL (CR-FMOL), the first federated MOO framework that enforces client-wise Pareto optimality through a novel preference-cone constraint. After local federated multi-gradient descent averaging (FMGDA) / federated stochastic multi-gradient descent averaging (FSMGDA) steps, each client transmits its aggregated task-loss vector as an implicit preference; the server then solves a cone-constrained Pareto-MTL sub-problem centred at the uniform vector, producing a descent direction that is Pareto-stationary for every client within its cone. Experiments on non-IID benchmarks show that CR-FMOL enhances client fairness, and although the early-stage performance is slightly inferior to FedAvg, it is expected to achieve comparable accuracy given sufficient training rounds.

Distributed gradient methods under heavy-tailed communication noise

We consider a standard distributed optimization problem in which networked nodes collaboratively minimize the sum of their locally known convex costs. For this setting, we address for the first time the fundamental problem of design and analysis of distributed methods to solve the above problem when inter-node communication is subject to \emph{heavy-tailed} noise. Heavy-tailed noise is highly relevant and frequently arises in densely deployed wireless sensor and Internet of Things (IoT) networks. Specifically, we design a distributed gradient-type method that features a carefully balanced mixed time-scale time-varying consensus and gradient contribution step sizes and a bounded nonlinear operator on the consensus update to limit the effect of heavy-tailed noise. Assuming heterogeneous strongly convex local costs with mutually different minimizers that are arbitrarily far apart, we show that the proposed method converges to a neighborhood of the network-wide problem solution in the mean squared error (MSE) sense, and we also characterize the corresponding convergence rate. We further show that the asymptotic MSE can be made arbitrarily small through consensus step-size tuning, possibly at the cost of slowing down the transient error decay. Numerical experiments corroborate our findings and demonstrate the resilience of the proposed method to heavy-tailed (and infinite variance) communication noise. They also show that existing distributed methods, designed for finite-communication-noise-variance settings, fail in the presence of infinite variance noise.

Distributed Sign Momentum with Local Steps for Training Transformers

Pre-training Transformer models is resource-intensive, and recent studies have shown that sign momentum is an efficient technique for training large-scale deep learning models, particularly Transformers. However, its application in distributed training or federated learning remains underexplored. This paper investigates a novel communication-efficient distributed sign momentum method with local updates. Our proposed method allows for a broad class of base optimizers for local updates, and uses sign momentum in global updates, where momentum is generated from differences accumulated during local steps. We evaluate our method on the pre-training of various GPT-2 models, and the empirical results show significant improvement compared to other distributed methods with local updates. Furthermore, by approximating the sign operator with a randomized version that acts as a continuous analog in expectation, we present an $O(1/\sqrt{T})$ convergence for one instance of the proposed method for nonconvex smooth functions.

Large Deviations and Improved Mean-squared Error Rates of Nonlinear SGD: Heavy-tailed Noise and Power of Symmetry

We study large deviations and mean-squared error (MSE) guarantees of a general framework of nonlinear stochastic gradient methods in the online setting, in the presence of heavy-tailed noise. Unlike existing works that rely on the closed form of a nonlinearity (typically clipping), our framework treats the nonlinearity in a black-box manner, allowing us to provide unified guarantees for a broad class of bounded nonlinearities, including many popular ones, like sign, quantization, normalization, as well as component-wise and joint clipping. We provide several strong results for a broad range of step-sizes in the presence of heavy-tailed noise with symmetric probability density function, positive in a neighbourhood of zero and potentially unbounded moments. In particular, for non-convex costs we provide a large deviation upper bound for the minimum norm-squared of gradients, showing an asymptotic tail decay on an exponential scale, at a rate $\sqrt{t} / \log(t)$. We establish the accompanying rate function, showing an explicit dependence on the choice of step-size, nonlinearity, noise and problem parameters. Next, for non-convex costs and the minimum norm-squared of gradients, we derive the optimal MSE rate $\widetilde{\mathcal{O}}(t^{-1/2})$. Moreover, for strongly convex costs and the last iterate, we provide an MSE rate that can be made arbitrarily close to the optimal rate $\mathcal{O}(t^{-1})$, improving on the state-of-the-art results in the presence of heavy-tailed noise. Finally, we establish almost sure convergence of the minimum norm-squared of gradients, providing an explicit rate, which can be made arbitrarily close to $o(t^{-1/4})$.

Nonlinear Stochastic Gradient Descent and Heavy-tailed Noise: A Unified Framework and High-probability Guarantees

We study high-probability convergence in online learning, in the presence of heavy-tailed noise. To combat the heavy tails, a general framework of nonlinear SGD methods is considered, subsuming several popular nonlinearities like sign, quantization, component-wise and joint clipping. In our work the nonlinearity is treated in a black-box manner, allowing us to establish unified guarantees for a broad range of nonlinear methods. For symmetric noise and non-convex costs we establish convergence of gradient norm-squared, at a rate $\widetilde{\mathcal{O}}(t^{-1/4})$, while for the last iterate of strongly convex costs we establish convergence to the population optima, at a rate $\mathcal{O}(t^{-\zeta})$, where $\zeta \in (0,1)$ depends on noise and problem parameters. Further, if the noise is a (biased) mixture of symmetric and non-symmetric components, we show convergence to a neighbourhood of stationarity, whose size depends on the mixture coefficient, nonlinearity and noise. Compared to state-of-the-art, who only consider clipping and require unbiased noise with bounded $p$-th moments, $p \in (1,2]$, we provide guarantees for a broad class of nonlinearities, without any assumptions on noise moments. While the rate exponents in state-of-the-art depend on noise moments and vanish as $p \rightarrow 1$, our exponents are constant and strictly better whenever $p < 6/5$ for non-convex and $p < 8/7$ for strongly convex costs. Experiments validate our theory, demonstrating noise symmetry in real-life settings and showing that clipping is not always the optimal nonlinearity, further underlining the value of a general framework.

Computational Imaging for Long-Term Prediction of Solar Irradiance

The occlusion of the sun by clouds is one of the primary sources of uncertainties in solar power generation, and is a factor that affects the wide-spread use of solar power as a primary energy source. Real-time forecasting of cloud movement and, as a result, solar irradiance is necessary to schedule and allocate energy across grid-connected photovoltaic systems. Previous works monitored cloud movement using wide-angle field of view imagery of the sky. However, such images have poor resolution for clouds that appear near the horizon, which reduces their effectiveness for long term prediction of solar occlusion. Specifically, to be able to predict occlusion of the sun over long time periods, clouds that are near the horizon need to be detected, and their velocities estimated precisely. To enable such a system, we design and deploy a catadioptric system that delivers wide-angle imagery with uniform spatial resolution of the sky over its field of view. To enable prediction over a longer time horizon, we design an algorithm that uses carefully selected spatio-temporal slices of the imagery using estimated wind direction and velocity as inputs. Using ray-tracing simulations as well as a real testbed deployed outdoors, we show that the system is capable of predicting solar occlusion as well as irradiance for tens of minutes in the future, which is an order of magnitude improvement over prior work.

Vehicle-to-Vehicle Charging: Model, Complexity, and Heuristics

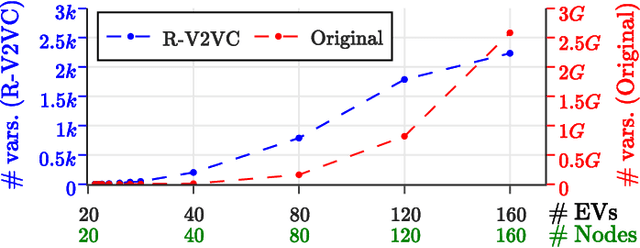
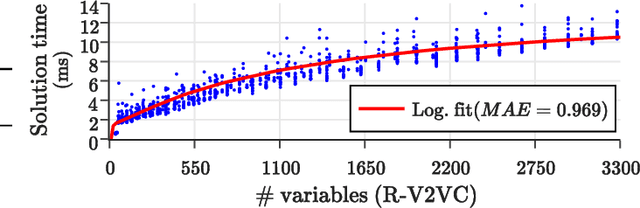
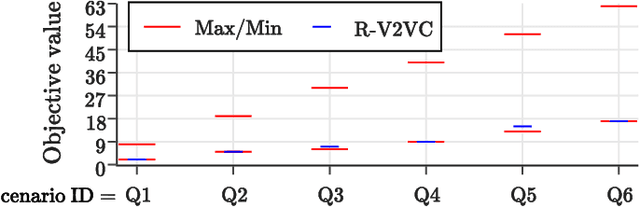
The rapid adoption of Electric Vehicles (EVs) poses challenges for electricity grids to accommodate or mitigate peak demand. Vehicle-to-Vehicle Charging (V2VC) has been recently adopted by popular EVs, posing new opportunities and challenges to the management and operation of EVs. We present a novel V2VC model that allows decision-makers to take V2VC into account when optimizing their EV operations. We show that optimizing V2VC is NP-Complete and find that even small problem instances are computationally challenging. We propose R-V2VC, a heuristic that takes advantage of the resulting totally unimodular constraint matrix to efficiently solve problems of realistic sizes. Our results demonstrate that R-V2VC presents a linear growth in the solution time as the problem size increases, while achieving solutions of optimal or near-optimal quality. R-V2VC can be used for real-world operations and to study what-if scenarios when evaluating the costs and benefits of V2VC.