S-ADDOPT: Decentralized stochastic first-order optimization over directed graphs

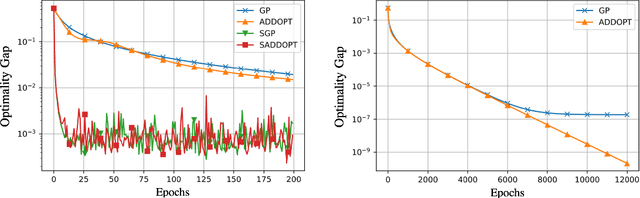
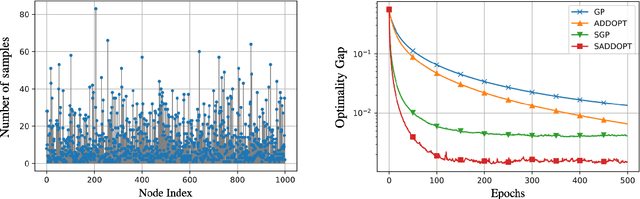
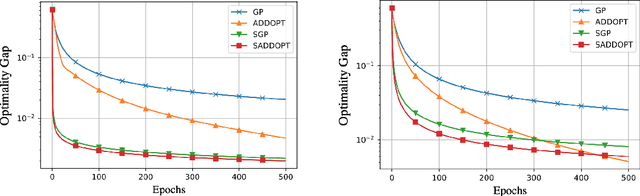
In this report, we study decentralized stochastic optimization to minimize a sum of smooth and strongly convex cost functions when the functions are distributed over a directed network of nodes. In contrast to the existing work, we use gradient tracking to improve certain aspects of the resulting algorithm. In particular, we propose the S-ADDOPT algorithm that assumes a stochastic first-order oracle at each node and show that for a constant step-size $\alpha$, each node converges linearly inside an error ball around the optimal solution, the size of which is controlled by $\alpha$. For decaying step-sizes $\mathcal{O}(1/k)$, we show that S-ADDOPT reaches the exact solution sublinearly at $\mathcal{O}(1/k)$ and its convergence is asymptotically network-independent. Thus the asymptotic behavior of S-ADDOPT is comparable to the centralized stochastic gradient descent. Numerical experiments over both strongly convex and non-convex problems illustrate the convergence behavior and the performance comparison of the proposed algorithm.