A hybrid variance-reduced method for decentralized stochastic non-convex optimization
Paper and Code
Feb 12, 2021
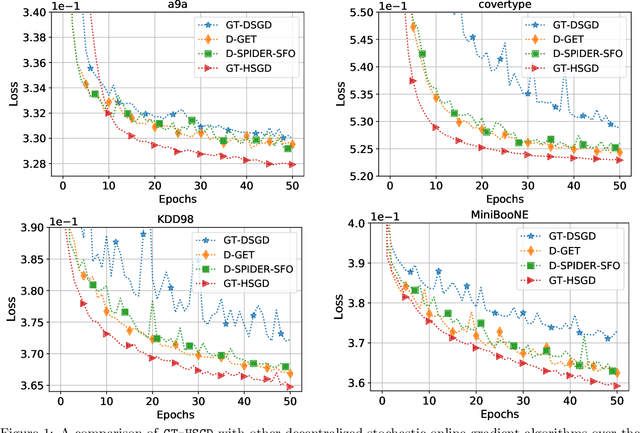
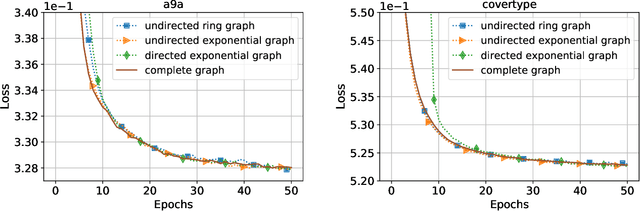
This paper considers decentralized stochastic optimization over a network of~$n$ nodes, where each node possesses a smooth non-convex local cost function and the goal of the networked nodes is to find an~$\epsilon$-accurate first-order stationary point of the sum of the local costs. We focus on an online setting, where each node accesses its local cost only by means of a stochastic first-order oracle that returns a noisy version of the exact gradient. In this context, we propose a novel single-loop decentralized hybrid variance-reduced stochastic gradient method, called \texttt{GT-HSGD}, that outperforms the existing approaches in terms of both the oracle complexity and practical implementation. The \texttt{GT-HSGD} algorithm implements specialized local hybrid stochastic gradient estimators that are fused over the network to track the global gradient. Remarkably, \texttt{GT-HSGD} achieves a network-independent oracle complexity of~$O(n^{-1}\epsilon^{-3})$ when the required error tolerance~$\epsilon$ is small enough, leading to a linear speedup with respect to the centralized optimal online variance-reduced approaches that operate on a single node. Numerical experiments are provided to illustrate our main technical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge