Gradient tracking and variance reduction for decentralized optimization and machine learning
Paper and Code
Feb 13, 2020

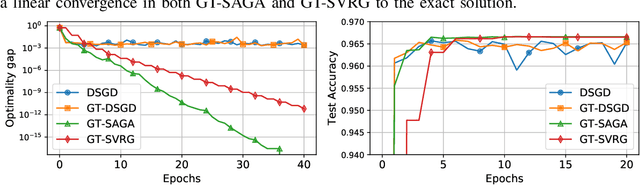

Decentralized methods to solve finite-sum minimization problems are important in many signal processing and machine learning tasks where the data is distributed over a network of nodes and raw data sharing is not permitted due to privacy and/or resource constraints. In this article, we review decentralized stochastic first-order methods and provide a unified algorithmic framework that combines variance-reduction with gradient tracking to achieve both robust performance and fast convergence. We provide explicit theoretical guarantees of the corresponding methods when the objective functions are smooth and strongly-convex, and show their applicability to non-convex problems via numerical experiments. Throughout the article, we provide intuitive illustrations of the main technical ideas by casting appropriate tradeoffs and comparisons among the methods of interest and by highlighting applications to decentralized training of machine learning models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge