HARE: HumAn pRiors, a key to small language model Efficiency

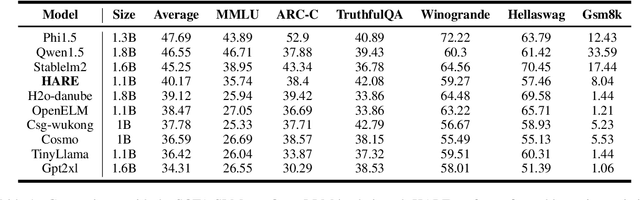
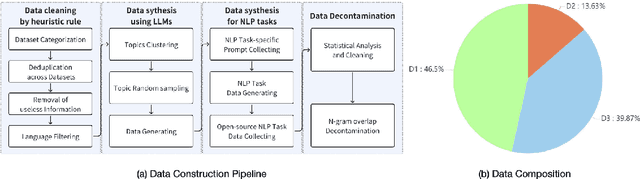
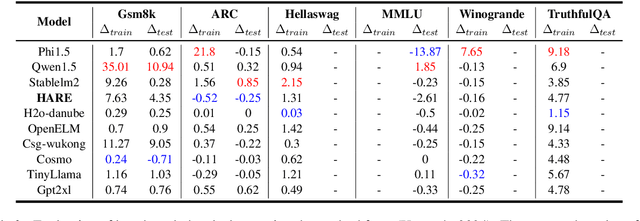
Human priors play a crucial role in efficiently utilizing data in deep learning. However, with the development of large language models (LLMs), there is an increasing emphasis on scaling both model size and data volume, which often diminishes the importance of human priors in data construction. Influenced by these trends, existing Small Language Models (SLMs) mainly rely on web-scraped large-scale training data, neglecting the proper incorporation of human priors. This oversight limits the training efficiency of language models in resource-constrained settings. In this paper, we propose a principle to leverage human priors for data construction. This principle emphasizes achieving high-performance SLMs by training on a concise dataset that accommodates both semantic diversity and data quality consistency, while avoiding benchmark data leakage. Following this principle, we train an SLM named HARE-1.1B. Extensive experiments on large-scale benchmark datasets demonstrate that HARE-1.1B performs favorably against state-of-the-art SLMs, validating the effectiveness of the proposed principle. Additionally, this provides new insights into efficient language model training in resource-constrained environments from the view of human priors.

Distributed Random Reshuffling Methods with Improved Convergence

This paper proposes two distributed random reshuffling methods, namely Gradient Tracking with Random Reshuffling (GT-RR) and Exact Diffusion with Random Reshuffling (ED-RR), to solve the distributed optimization problem over a connected network, where a set of agents aim to minimize the average of their local cost functions. Both algorithms invoke random reshuffling (RR) update for each agent, inherit favorable characteristics of RR for minimizing smooth nonconvex objective functions, and improve the performance of previous distributed random reshuffling methods both theoretically and empirically. Specifically, both GT-RR and ED-RR achieve the convergence rate of $O(1/[(1-\lambda)^{1/3}m^{1/3}T^{2/3}])$ in driving the (minimum) expected squared norm of the gradient to zero, where $T$ denotes the number of epochs, $m$ is the sample size for each agent, and $1-\lambda$ represents the spectral gap of the mixing matrix. When the objective functions further satisfy the Polyak-{\L}ojasiewicz (PL) condition, we show GT-RR and ED-RR both achieve $O(1/[(1-\lambda)mT^2])$ convergence rate in terms of the averaged expected differences between the agents' function values and the global minimum value. Notably, both results are comparable to the convergence rates of centralized RR methods (up to constant factors depending on the network topology) and outperform those of previous distributed random reshuffling algorithms. Moreover, we support the theoretical findings with a set of numerical experiments.

Text-to-Image Diffusion Models can be Easily Backdoored through Multimodal Data Poisoning

With the help of conditioning mechanisms, the state-of-the-art diffusion models have achieved tremendous success in guided image generation, particularly in text-to-image synthesis. To gain a better understanding of the training process and potential risks of text-to-image synthesis, we perform a systematic investigation of backdoor attack on text-to-image diffusion models and propose BadT2I, a general multimodal backdoor attack framework that tampers with image synthesis in diverse semantic levels. Specifically, we perform backdoor attacks on three levels of the vision semantics: Pixel-Backdoor, Object-Backdoor and Style-Backdoor. By utilizing a regularization loss, our methods efficiently inject backdoors into a large-scale text-to-image diffusion model while preserving its utility with benign inputs. We conduct empirical experiments on Stable Diffusion, the widely-used text-to-image diffusion model, demonstrating that the large-scale diffusion model can be easily backdoored within a few fine-tuning steps. We conduct additional experiments to explore the impact of different types of textual triggers. Besides, we discuss the backdoor persistence during further training, the findings of which provide insights for the development of backdoor defense methods.

One Transformer Fits All Distributions in Multi-Modal Diffusion at Scale

This paper proposes a unified diffusion framework (dubbed UniDiffuser) to fit all distributions relevant to a set of multi-modal data in one model. Our key insight is -- learning diffusion models for marginal, conditional, and joint distributions can be unified as predicting the noise in the perturbed data, where the perturbation levels (i.e. timesteps) can be different for different modalities. Inspired by the unified view, UniDiffuser learns all distributions simultaneously with a minimal modification to the original diffusion model -- perturbs data in all modalities instead of a single modality, inputs individual timesteps in different modalities, and predicts the noise of all modalities instead of a single modality. UniDiffuser is parameterized by a transformer for diffusion models to handle input types of different modalities. Implemented on large-scale paired image-text data, UniDiffuser is able to perform image, text, text-to-image, image-to-text, and image-text pair generation by setting proper timesteps without additional overhead. In particular, UniDiffuser is able to produce perceptually realistic samples in all tasks and its quantitative results (e.g., the FID and CLIP score) are not only superior to existing general-purpose models but also comparable to the bespoken models (e.g., Stable Diffusion and DALL-E 2) in representative tasks (e.g., text-to-image generation).

Distributed Stochastic Optimization under a General Variance Condition

Distributed stochastic optimization has drawn great attention recently due to its effectiveness in solving large-scale machine learning problems. However, despite that numerous algorithms have been proposed with empirical successes, their theoretical guarantees are restrictive and rely on certain boundedness conditions on the stochastic gradients, varying from uniform boundedness to the relaxed growth condition. In addition, how to characterize the data heterogeneity among the agents and its impacts on the algorithmic performance remains challenging. In light of such motivations, we revisit the classical FedAvg algorithm for solving the distributed stochastic optimization problem and establish the convergence results under only a mild variance condition on the stochastic gradients for smooth nonconvex objective functions. Almost sure convergence to a stationary point is also established under the condition. Moreover, we discuss a more informative measurement for data heterogeneity as well as its implications.

CEDAS: A Compressed Decentralized Stochastic Gradient Method with Improved Convergence

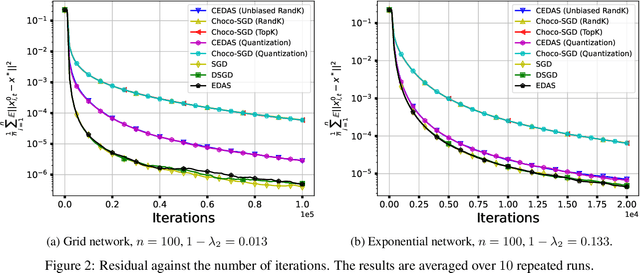
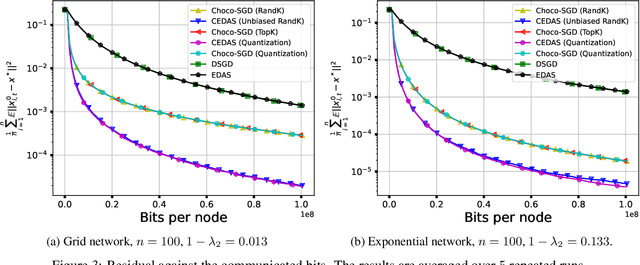
In this paper, we consider solving the distributed optimization problem over a multi-agent network under the communication restricted setting. We study a compressed decentralized stochastic gradient method, termed ``compressed exact diffusion with adaptive stepsizes (CEDAS)", and show the method asymptotically achieves comparable convergence rate as centralized SGD for both smooth strongly convex objective functions and smooth nonconvex objective functions under unbiased compression operators. In particular, to our knowledge, CEDAS enjoys so far the shortest transient time (with respect to the graph specifics) for achieving the convergence rate of centralized SGD, which behaves as $\mathcal{O}(nC^3/(1-\lambda_2)^{2})$ under smooth strongly convex objective functions, and $\mathcal{O}(n^3C^6/(1-\lambda_2)^4)$ under smooth nonconvex objective functions, where $(1-\lambda_2)$ denotes the spectral gap of the mixing matrix, and $C>0$ is the compression-related parameter. Numerical experiments further demonstrate the effectiveness of the proposed algorithm.

Alignment-Uniformity aware Representation Learning for Zero-shot Video Classification

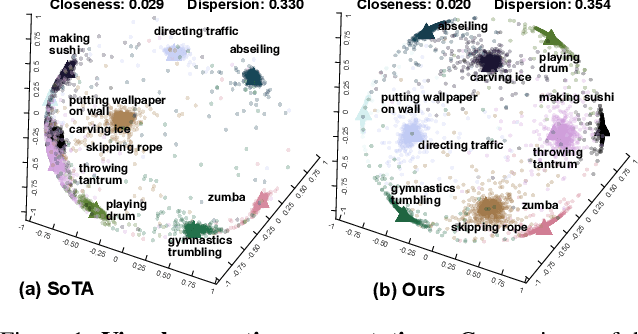
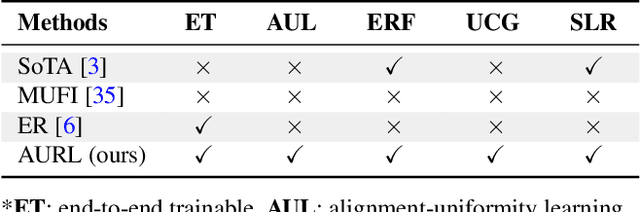
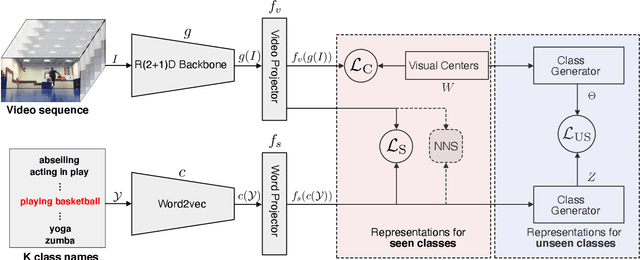
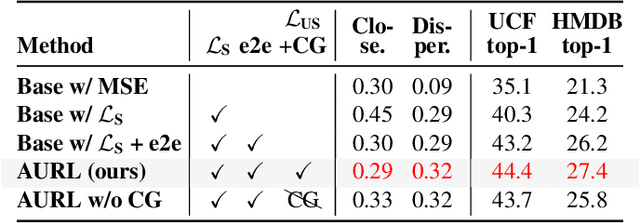
Most methods tackle zero-shot video classification by aligning visual-semantic representations within seen classes, which limits generalization to unseen classes. To enhance model generalizability, this paper presents an end-to-end framework that preserves alignment and uniformity properties for representations on both seen and unseen classes. Specifically, we formulate a supervised contrastive loss to simultaneously align visual-semantic features (i.e., alignment) and encourage the learned features to distribute uniformly (i.e., uniformity). Unlike existing methods that only consider the alignment, we propose uniformity to preserve maximal-info of existing features, which improves the probability that unobserved features fall around observed data. Further, we synthesize features of unseen classes by proposing a class generator that interpolates and extrapolates the features of seen classes. Besides, we introduce two metrics, closeness and dispersion, to quantify the two properties and serve as new measurements of model generalizability. Experiments show that our method significantly outperforms SoTA by relative improvements of 28.1% on UCF101 and 27.0% on HMDB51. Code is available.

Distributed Random Reshuffling over Networks

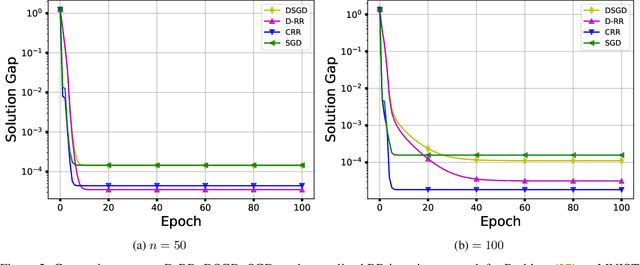
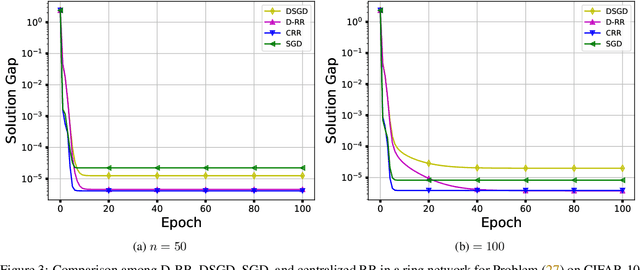
In this paper, we consider the distributed optimization problem where $n$ agents, each possessing a local cost function, collaboratively minimize the average of the local cost functions over a connected network. To solve the problem, we propose a distributed random reshuffling (D-RR) algorithm that combines the classical distributed gradient descent (DGD) method and Random Reshuffling (RR). We show that D-RR inherits the superiority of RR for both smooth strongly convex and smooth nonconvex objective functions. In particular, for smooth strongly convex objective functions, D-RR achieves $\mathcal{O}(1/T^2)$ rate of convergence (here, $T$ counts the total number of iterations) in terms of the squared distance between the iterate and the unique minimizer. When the objective function is assumed to be smooth nonconvex and has Lipschitz continuous component functions, we show that D-RR drives the squared norm of gradient to $0$ at a rate of $\mathcal{O}(1/T^{2/3})$. These convergence results match those of centralized RR (up to constant factors).

Provably Accelerated Decentralized Gradient Method Over Unbalanced Directed Graphs

In this work, we consider the decentralized optimization problem in which a network of $n$ agents, each possessing a smooth and convex objective function, wish to collaboratively minimize the average of all the objective functions through peer-to-peer communication in a directed graph. To solve the problem, we propose two accelerated Push-DIGing methods termed APD and APD-SC for minimizing non-strongly convex objective functions and strongly convex ones, respectively. We show that APD and APD-SC respectively converge at the rates $O\left(\frac{1}{k^2}\right)$ and $O\left(\left(1 - C\sqrt{\frac{\mu}{L}}\right)^k\right)$ up to constant factors depending only on the mixing matrix. To the best of our knowledge, APD and APD-SC are the first decentralized methods to achieve provable acceleration over unbalanced directed graphs. Numerical experiments demonstrate the effectiveness of both methods.

Compressed Gradient Tracking for Decentralized Optimization Over General Directed Networks

In this paper, we propose two communication-efficient algorithms for decentralized optimization over a multi-agent network with general directed network topology. In the first part, we consider a novel communication-efficient gradient tracking based method, termed Compressed Push-Pull (CPP), which combines the Push-Pull method with communication compression. We show that CPP is applicable to a general class of unbiased compression operators and achieves linear convergence for strongly convex and smooth objective functions. In the second part, we propose a broadcast-like version of CPP (B-CPP), which also achieves linear convergence rate under the same conditions for the objective functions. B-CPP can be applied in an asynchronous broadcast setting and further reduce communication costs compared to CPP. Numerical experiments complement the theoretical analysis and confirm the effectiveness of the proposed methods.